经常听到学生抱怨“数学课太枯燥,除概念、公式、定理、图形就没什么了,还那么多要记忆的,我们的脑子又不是电脑,就算勉强记住,也不会用。”到底造成学生学习数学困难的原因是什么?不难发现初高中生要学的内容越来越多,且在学习的过程中不加以梳理,只是杂乱无章的堆在脑子里,最终直接导致学习效率低下,这正是大多数初高生存在的最大问题。所以要想提初高生的数学成绩,
一是要教会学生如何梳理知识点,形成一个知识体系;
二是在教学中尽量运用直观教学,增加数学的趣味性,克服数学抽象的弊病。
而思维导图的提出,正满足了这一需要。思维导图是由英国著名心理学家托尼·巴赞于1970年提出。它运用线条、色彩、图像、联想功能表示出事物间的联系,具体操作过程就是把各级主题的关系用相互隶属与相关的层级图表现出来,把主题关键词与图像、颜色等建立记忆链接,以直观形象的方式进行表达和思考,非常接近人的自然思维过程。思维导图运用在数学教学中,为学生提供了思考框架,可以帮助学生构建完整有效的知识网络,突破了传统的线性思维对思维潜能的束缚,对培养发散性思维、提高记忆力、创造能力和归纳总结分析的能力十分有利。
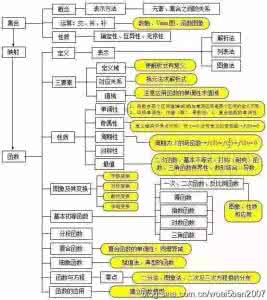
在“章”前应用——提纲挈领
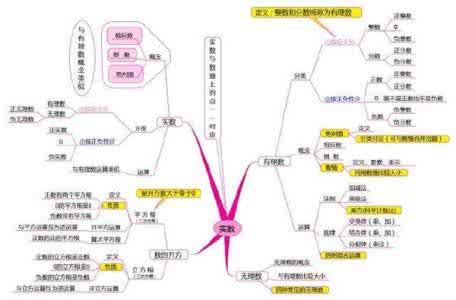
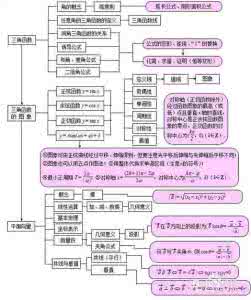
以高中数学第三章《三角函数》这一章的教学为例,可以在讲前出示思维导图:把这一章要掌握的知识点按照彼此内在的联系列出,使学生对新的学习方向和内容有一个大致了解,心中有数,有的放矢。同时也可降低学生对新内容学习的恐惧,让学生发现其实只要掌握一个点,顺着这个方向,像蜘蛛吐丝一样逐条解决,是很容易达到大纲要求的。
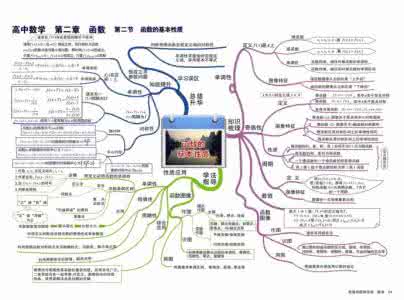
在“节”前应用——明确目标
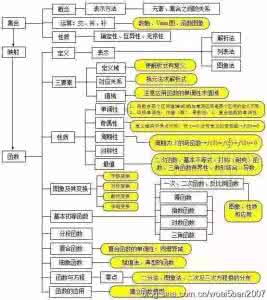
思维导图还可用到每一小节的教学中。以《三角函数》里的一节《任意角与弧度制》为例,根据思维导图方便学生直观的复习上节课知识,还可事先明确学习目标,再运用类比、对比、迁移等方法进行新内容的教学,降低了学习难度,这样做使学生更好的理解任意角和弧度制的区别与联系,更好地掌握研究三角函数的方法——数形结合思想的运用。
在“尾”处应用——总结提高
最后通过思维导图,帮助学生理顺知识,突出重难点,同时进行自查,及时查漏补缺。有了思维导图的介入,使学生思路更加清晰,思维进一步得到升华,为课堂教学画上了一个完美的句号。
在“记”课堂笔记中的应用-----融汇贯通
思维导图还可以让学生运用在记笔记方面,只记要点和关键词,这样就不用一整句一整句的记录,用自己可以看得懂的符号或代号来表达,不仅可以达到速记的效果,还可以省出大部分时间用于认真听讲,不会因为记笔记而无法消化老师所讲的内容,顾此失彼,得不偿失。
在总复习中的应用
在学完第八章三角函数后,可用思维导图将角和三角函数之间建立联系,关键词我确定为“十字”图形,因为这个在画角(运用“十字”图形方便角的旋转和角的终边的确定)和三角函数(“十字”图形即代表直角坐标系)中都有用到,这样做将整节知识点联系起来,形成整体框架,在不看书的情况下,大脑也能随时反应出各个主要部分知识在这门课程中的位置,一旦形成清晰的整体框架和完整的知识体系,这门课程就容易进步了。
在思维导图的帮助下,学生学会独立思考,逐渐培养学生运用知识解决问题的能力,进入“会学习、学好习、学习好”的佳境。
 爱华网
爱华网