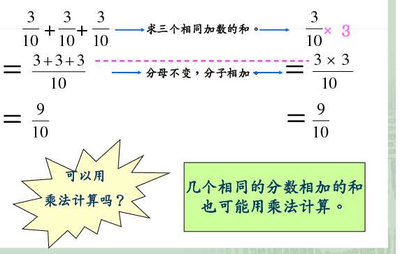
刚刚进入初中的时候,我的成绩差得一塌糊涂,在班上的排名只能倒着数。成绩糟糕的原因现在已经不清楚了。我所在的是一个“尖子班”,看我适应不了,班主任跑到我家里来动员我是否考虑转到普通班去。当时不明白,现在揣测,班主任要我转班估计是想踢开我这个后腿上的累赘。父母当着老师的面给了我一通板子,并要我发誓以后好好学习。抹干眼泪后,我带着挑战和对父母的许诺开始了新的一个学期。就在这个学期,我们开始学习平面几何。这门课程挽救了我,使我免于堕落到普通班去和那帮整天打打闹闹的孩子们混日子的命运。
实际上开始的时候,我发育迟缓的理解力面对平面几何多少有些吃力,我不太弄得懂里面那些命题的真正含义。是一次考试,准确地说是一道题目,在偶然间使我的悟性获得了苏醒。
半期考试的数学试卷上的最后一个题目是一幅图:离一条马路一段距离处有一口井,一个小孩手里拎着一桶水站在水井边。题目问:要用最短时间走到马路上,这个小孩该怎么走?
马上我就想到平面几何中的一个命题:“由一点到一条直线的距离垂直线最短。”我给出了正确的答案。
那次数学考试的成绩我名列前茅,估计是这道题目只是被很少的人破解,而我是其中之一。从此我成为了班上的优秀学生,老师和同学投给了我赞赏的目光。我完成了一个类似于丑小鸭到白天鹅的蜕变。
而我最大的收获是,因为做对这道题目,我一下子全明白了平面几何的所有命题。我知道了将经验中的事物比如“水井”对应到数学中的某一个元素比如“点”。我懂得了抽象的思维方式,我智力上蒙昧的少年时代结束了。
罗素说过:“一个人越是研究几何学,就越能看出它们是多么值得赞赏。”我想罗素之所以这么说,是因为平面几何曾经救了他一命的缘故。
就跟我在学习平面几何的时候差不多大的年龄,天知道是什么缘故,这个养尊处优的贵族子弟鬼迷心窍,想要自杀来结束自己那份下层社会人家的孩子巴望一辈子都够不到的幸福生活。在上吊或者抹脖子之前,头戴假发的小子想到做最后一件事情,那就是了解一下平面几何到底有多大迷人的魅力。而这个魅力是之前他的哥哥向他吹嘘的。估计他的哥哥将平面几何与人生的意义搅和在一起向他做了推介,不然万念俱灰的的头脑怎么会在离开之前想到去做最后的光顾?而罗素真的一下被迷住了,厌世的念头因为沉湎于平面几何而被淡化,最后竟被遗忘了。
罗素毕竟是罗素。平面几何对于我的意义只是发掘了一个成绩本来不错的中学生的潜力,为我解开了智力上的扭结;而在罗素那里,这门知识从一开始就使这个未来的伟大的怀疑论者显露了执拗的本性。他反对不加考察就接受平面几何的公理,在与哥哥的反复争论之后,只是他的哥哥使他确信不可能用其他的方法一步步由这样的公理来构建庞大的平面几何的体系的以后,他才同意接受这些公理。
公元前334年,年轻的亚历山大从马其顿麾师东进,短短的时间就建立了一个从尼罗河到印度河的庞大帝国。随着他的征服,希腊文明传播到了东方,开始了一个新的文明时代即“希腊化时代”,这时希腊文明的中心也从希腊本土转移到了东方,准确地说,是从雅典转移到了埃及的亚历山大城。正是在这个城市,诞生了“希腊化时代”最为杰出的科学成就,其中就包括欧几里德的几何学。因为他的成就,平面几何也被叫作“欧氏几何”。
“欧氏几何”以它无与伦比的完美体系一直被视为演绎知识的典范,哲学史家更愿意把它看作是古代希腊文化的结晶。它由人类理性不可辩驳的几个极其简单的“自明性公理”出发,通过严密的逻辑推理,演绎出一连串的定理,这些在结构上紧密依存的定理和作为基础的几个公理一起构筑了一个庞大的知识体系。世间事物的简洁之美无出其右。
也许正是因为它的完美,直到十九世纪,在西方,《欧氏几何》一直是仅次于《圣经》的出版物,由此可见它的流行程度。然而,平面几何的真正意义,它对世界文明产生的影响岂止于此。
可以这么说,如果没有欧氏几何,现代社会一切价值构建是不可想象的,起码启蒙时代崭新的观念在驳斥旧有事物的时候就不会那么振振有辞。
从对于后世的意义的角度来讲,平面几何的最大价值在于提出了“自明性公理”。人类知识有两个部分,其中绝大部分是“定理”,所谓“定理”是推理出来的结论,由这样的“定理”可以一直回溯到不被别的命题限定而直接呈现在人类理性中的“公理”。这样的“自明性公理”之所以是自明的,是因为它们不可证明而在人类的理性看来却具有不可辩驳的正确性。譬如说,平面几何中作为公理出现的“两点之间的距离直线最短”,就是这样的“自明”的命题。往往这样的命题并不多,作为庞大的平面几何的体系基础的这样的“自明性公理”就只有简单的五条。
这样意义就巨大了。一个命题、一个观念、一个思想如果被考察是“自明”的,那么它就会借助人类的理性获得不可辩驳的力量。
寻找“自明性”基础的最初努力在平面几何之后是罗马的自然法。历史学家认为,罗马法之所以成为后世法律的合理源头是因为罗马法找到自然法作为自己的基础。自然法是哲学思考而不是司法实践的产物。当时罗马的流行哲学斯多噶派思考了这样的问题:他们断言,所有的人就其天性而论是相同的,任何人都有资格享有某些基本的权利,这些权利是自然赋予的,因而也就是“自明的”,对于这些权利政府无权违背。西塞罗宣称:“真正的法律是广泛流传于一切人之中的、永恒不变的、与天性相一致的的正常理智。我们既不可以对它稍加废除,我们也无权通过元老院或人民使自己不受它的约束。”从这里我们可以看出,罗马人为自己的法律选择的基础不是某一阶级的需要、也不是应动荡时代的某些要求而随意地进行改变,而是在法律确立之初就寻找到稳固的理性的“自明性”基础。实际上,近代社会的基本精神在罗马人那里就已经开始有了它的规模。
18世纪是人类的现代价值观念拿着自己的武器向旧秩序宣战的时代。那个时代“一切都要拿到理性的审判台前进行审判”,实际上所谓“审判”不如说是“自呈”,也就是说能否在理性面前呈现自己是否“自明”。如果是自明的,就是理性不可辩驳的。这样公平而且具有说服力。所以罗素说:“‘独立宣言’说:‘我们认为这些真理是自明的:人人生而平等。’,其本身就脱胎于欧几里德。”他还说:“十八世纪天赋人权的学说,就是一种在政治方面追求欧几里德式的公理。”(罗素《西方哲学史》)
推荐: 记者
 爱华网
爱华网