科学的肢体语言——图像法
图像是一种科学语言。相对于文字语言与数学语言而言,图像语言具有形象直观、明晰易懂、富于动感、有极强的启发性等特点。图像作为一种增进理解的思维辅助工具,被用于一切科学领域之中,应用极其广泛。

在物理学中应用图像处理问题的例子非常多,而且其功能是非常强大的,以电场线描述电场为例,即可见一斑。作为特殊物质形式的电场,我们无法用常态物质的一些基本属性,如密度、硬度、颜色、气味或化学性质等进行描述,但这种特殊物质是有它的基本属性的,我们似乎难以用清晰的文字语言与数学语言进行相应的描述,而天才的物理学家法拉第则用一幅电场线的图形将电场的相关特性一下子展现在我们面前。而且,有的物理问题几乎无法通过文字与数学加以描述,只有借助图像才能作出相应的描述,如复杂的电路结构图。
图像有时不仅仅是辅助思维的工具,而且还是求解问题的重要手段。利用图像法解题的优点在于可以直观地观察出物理过程的动态特征,使思路更加清晰,更容易找到巧妙的解题途径。
物理学中常用的图像形式有很多,如结构图、示意图、隔离图、状态图、位形图、布局图、 运行图、相图、光路图、坐标图等等,这些图形根据不同的需要,或给出条件信息,或呈现状态特征,或显示变化过程,或描述最终结果。不过,从图像的给出方式来看,这些图形大体上可以分为三类。
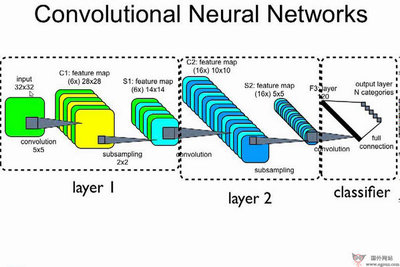
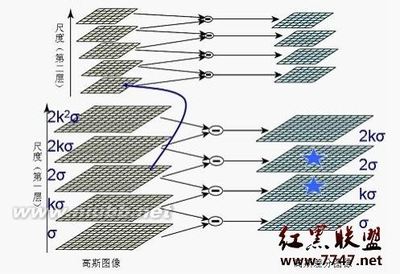
第一类是描述模型结构与运行过程的示意图。
所有的物理概念都是建立在一定的物理模型之上的,而对物理模型的描述几乎无法绕开物理模型与过程的示意图。我们知道,在解题时,题文中一句“如图所示”所包含的信息量,有时是无法用文字信息量来进行计量的,(快速提高物理成绩的奇书——巧学妙解王高中物理)它能让我们瞬间明白物理过程是在什么样的背景下发生的。 而对物理状态与过程描述的示意图,有助于我们认识物理过程的发生与进展,明晰不同阶段的特点及所遵循的规律,帮助我们找到解题的突破口。
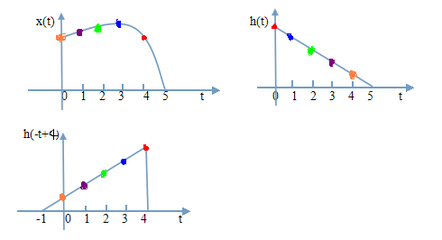
第二类是矢量及显示几何特征的图像。
对于是矢量的物理量,它们的运算遵循平行四边形法则,即几何法则,因此,图解它们是一种非常有效的途径。特别是一些动态问题,用矢量图解法处理有着其他方法不可替代的优势。
另外,在交流电路里,我们经常会遇到两个简谐量(两个电压或者两个电流)的合成问题。由于一个简谐量与一个旋转矢量对应,则所有简谐量的合成均可采用矢量图解法。
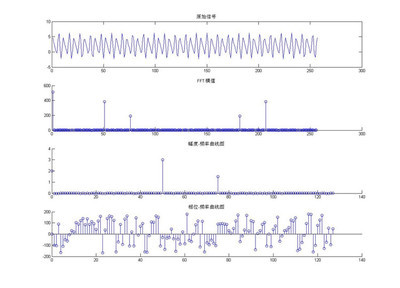
第三类是函数图像。
物理规律的描述,常用到函数解析式,同样,这些函数关系式也常用对应的函数图像来描述。中学物理中涉及的这些图像,常用二维直角坐标系来表示,这时一个图像除了直接明显地显示出两个坐标轴所代表的物理量的对应关系外,从图上往往还可以挖掘出更丰富的; 物理内涵,能正确地把握物理图像中丰富的物理内涵,无疑也是提高我们解题能力的一个很 值得注意的方面。
中学物理中常见的函数图像有:正比例图像、反比例图像、一次函数图像、二次函数图像、正弦(或余弦)函数图像等等。
对于这类图像应注意:
①搞清图像研究的是什么,并根据题目所反映的物理规律确定物理量之间的函数关系;
②明确图像的物理意义:识别坐标原点、横坐标、纵坐标及其标度所代表的物理量及其物理意义,明确物理图像的中点、线段、截距、峰值、切线与切点、法线、斜率、曲率与曲率半径、交点、拐点、极值点与极值、面积等的物理意义;
③对图像进行分析、比较、判断,找出规律,得出结论。常用方法有观察分析法、比较判断法、分析计算法等。
有的物理问题和求解涉及我们在中学阶段无法用代数求解的超越方程或只知其函数图像而并不知其代数式的函数,在遇到这种问题时,直接列方程求解是相当困难的,而图像法是解决这类问题的有效方法之一。
另外,用图像来处理实验数据也是物理研究中最为基本、也最为常见的方法,要求大家努力学习,力求掌握。
 爱华网
爱华网