高等数学常用极限公式 高等数学常用极限公式 高等数学常用极限求法

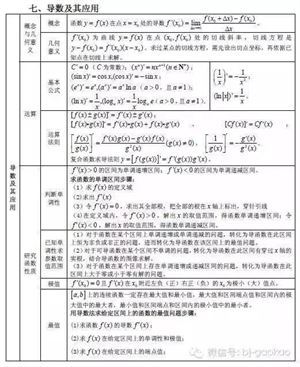
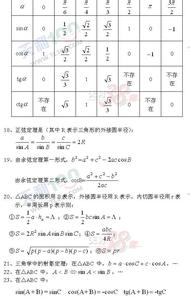
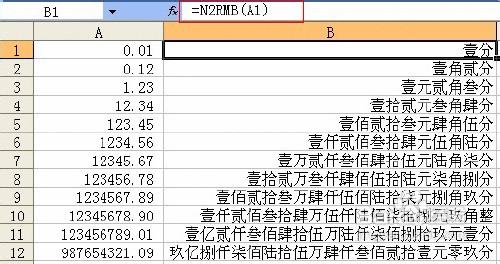
求

摘要: 本文就关于求函数极限的方法和技巧作了一个比较全面的概括、综合。 关键词：函数极限

引言

在数学分析与微积分学中,极限的概念占有主要的地位并以各种形式出现而贯穿全部内容,因此掌握好极限的求解方法是学习数学分析和微积分的关键一环。本文就关于求函数极限的方法和技巧作一个比较全面的概括、综合,力图在方法的正确灵活运用方面,对读者有所助益。

主要内容

一、求函数极限的方法

1、运用极限的定义

例: 用极限定义证明:

x23x2lim1 x2x2

x23x2x24x4证: 由 x2x2



0 x22x2x2 取 则当0x2 时,就有

x23x2  x2

由函数极限定义有:

1

limx23x2

2x21 x

2、利用极限的四则运算性质

若 limxxf(x)A limxxg(x)B 00

(I)limxxf(x)g(x) limf(x)limxg(x)AB 0xx0x0

(II)limxxf(x)g(x)limxf(x)limg(x)AB 0x0xx0

(III)若 B≠0 则： limf(x)limxf(x)

xg(x)x0

limA x0

xxg(x)B0

IV）limxxcf(x)climf(x)cA （c为常数） 0xx0

上述性质对于x,x,x时也同样成立 例：求 limx23x5

4 x2x

解: limx23x5=22325

2x4245

2 x3、约去零因式（此法适用于xx0

0时,0型）

例: 求xlimx3x216x202x37x216x12

3

解:原式=x3x210x(2x26x20)

xlim2x35x26x

(2x210x12) lim(x2)(x23x10)

(x2)(x25x6) x2

2 （ =

(x5)(x2)(x23x10)=lim= limx2(x2)(x3)x2(x25x6)

=lim

4、通分法（适用于型）

例: 求 lim(x2x2x57 x341) 4x22x

解: 原式=lim4(2x) x2(2x)(2x)

(2x) x2(2x)(2x)

11 x22x4 =lim =lim

5、利用无穷小量性质法（特别是利用无穷小量与有界量之乘积仍为无穷小量的性质） 设函数f(x)、g(x) 满足：

（I）limf(x)0 xx0

(II) g(x)M (M为正整数)

则：limg(x)f(x)0 xx0

例: 求 limxsinx01 x

解: 由 limx0 而 sinx011 x

故 原式 =limxsinx010 x

6、利用无穷小量与无穷大量的关系。

3

（I）若：limf(x) 则 lim10 f(x)

(II) 若: limf(x)0 且 f(x)≠0 则 lim

例: 求下列极限

① lim1 f(x)11 ②lim xx5x1x1

解: 由 lim(x5) 故 lim

7、等价无穷小代换法 10 xxx51由 lim(x1)0 故 lim= x1x1x1

设,',,' 都是同一极限过程中的无穷小量，且有：

~,~'， ''

lim' 存在， 

'

则 lim 也存在，且有lim= lim' 

1cosx2

例:求极限lim2 x0xsinx2

(x2)2

解: sinx~x, 1cosx~ 2222

(x2)2

11cosx2lim = 22x0x2sinx22xx

注： 在利用等价无穷小做代换时，一般只在以乘积形式出现时可以互换，若以和、差出现时，不要轻易代换，因为此时经过代换后，往往改变了它的无穷小量之比的“阶数”

8、利用两个重要的极限。

4

(A)limsinx

x0x1 (B)limx(11x)xe

但我们经常使用的是它们的变形：

(A')limsin(x)

(x)1,((x)0)

(B')lim(11

(x))(x)e,((x))

例：求下列函数极限

(1)、limax1 lncos

x0x(2)、limax

x0lncosbx

x1u,则 xln(1u)ax

解：（1）令a1ulna

lna 于是xln(1u)

又当x0时，u0

故有：limax1

x0xlimulna

u0ln(1u)limlnalna

u0ln(1u)limu01lna

uln(1u)u

(2)、原式limln[(1(cosax1)]

(cosbx1)] x0ln[1

limln[(1(cosax1)]cosbx1

x0cosax1cosax1

ln[1(cosbx1)]

cosbx1

limcosbx1

x0cosax1

sin2ax

2sin2x(ax)2(bx)2

limlimb2



2sin22 x0bx0baa

2xsin2

x(2x)2

(bx)2

2

、利用函数的连续性（适用于求函数在连续点处的极限）。

5 9

(i)若f(x)在xx0处连续，则limxxf(x)f(x0)

(ii)若f[(x)]是复合函数，又limxx(x)a且 0

f(u)在ua处连续，则limxxf((x))f[limx(x)]f(a)0x0

例：求下列函数的极限

(1)、limexcosx5 （2） x01x2ln(1x)limln1(x)

x0x 解：由于x0属于初等函数f(x)excosx5

1x2ln(1x)的定义域之内。

故由函数的连续性定义有：

limexcosx5

x01x2ln(1x)f(0)6

1

(2)、由ln(1x)

xln(1x)x

1

令x(1x)x故有：

11

limln(1x)

x0xlimx0ln(1x)xln(limx0(1x)x)lne1

10、变量替换法（适用于分子、分母的根指数不相同的极限类型）特别地有：l

limxk1

x1nmlnk m、n、k、l 为正整数。 xm1

例：求下列函数极限

① lim1x2x3x

x11x(m 、n N) ②limx(2x1)1

解: ①令 t=x 则当x1 时 t1,于是

原式=lim1tm(1t)(1tt2tm1)

t11tnlimt1(1t)(1tt2tn1)m

n ②由于lim2x3

x(2x1)x1=limx(12x12x1)

6

令：2x1111 则 x1 2tt2

112x3x12x1)=lim(1)=lim(1t)t2 lim(x2x1xt02x1

1

t12 =lim(1t)lim(1t)e1e t0t0

11、 利用函数极限的存在性定理 定理: 设在x0的某空心邻域内恒有 g(x)≤f(x)≤h(x)

limxxg(x)limh(x)A 0xx0

则极限 limxxf(x) 存在, 且有 0

limxxf(x)A 0

: 求 xlimxn例ax (a>1,n>0)

解: 当 x≥1 时,存在唯一的正整数k,使

≤x≤k+1

于是当 n>0 时有: xn(k1)n

axak

xnkn

及 akn1

xak1aka

又 当x时,k 有 (k1)n(k1)n

klimakklimak1a0a0

knkn

及 klim11ak1 klimaka0a0 且有:

7 k



xnlim=0 xax

12、用左右极限与极限关系(适用于分段函数求分段点处的极限，以及用定义求极限等情形)。

f(x)及右极定理：函数极限limf(x)存在且等于A的充分必要条件是左极限limxx0xx0

限limxxf(x)都存在且都等于A。即有： 0

xlimxf(x)Alimf(x)=lim0xf(x)=A xx0x0

12ex,x0

例：设f(x)=xx,0x1 求limf(x)

xx0及limx1f(x)

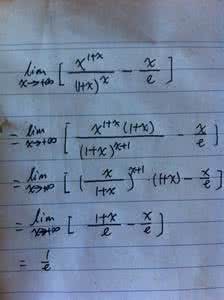
x2,x1

解：xlim0f(x)xlim0(12ex)1

xlim0f(x)xx xlim0(x)xlim0(x1)1

由limx0f(x)limx0f(x)1

limx0f(x)1 又limf(x)limxx

x1x1xlimx1x1)0

lim2

x1f(x)limx1x1

由f(10)f(10)

limx1f(x)不存在

13、罗比塔法则（适用于未定式极限）

定理：若

8

(i)limf(x)0,limg(x)0xx0xx0

(ii)f与g在x0的某空心邻域u0(x0)内可导，且g'(x)0

f'(x)(iii)lim'A(A可为实数，也可为或），则 xx0g(x)

f(x)f'(x)limlim'Axx0g(x)xx0g(x)

此定理是对0型而言，对于函数极限的其它类型，均有类似的法则。 0

0,时不可求导。 0注：运用罗比塔法则求极限应注意以下几点： 1、 要注意条件，也就是说，在没有化为

2、 应用罗比塔法则，要分别的求分子、分母的导数，而不是求整个分式的导数。

3、 要及时化简极限符号后面的分式，在化简以后检查是否仍是未定式，若遇到不是

未定式，应立即停止使用罗比塔法则，否则会引起错误。

f'(x)4、当lim' 不存在时，本法则失效，但并不是说极限不存在，此时求极限须用xag(x)

另外方法。

例： 求下列函数的极限 ex(12x)①limx0ln(1x2) ②lim

lnx(a0,x0) xxa2x解：①令f(x)= e(12x), g(x)= ln(1x)

'f(x)e(12x)

"x'x, g(x)"2x 1x222(1x) f(x)e(12x),g(x)22(1x)由于f(0)f(0)0,g(0)g(0)0

但f(0)2,g(0)2

从而运用罗比塔法则两次后得到 ""''

9

ex(12x)limx0ln(1x2)ex(12x)limx02x

1x2

a

xex(12x)limx02(1x2)(1x2)221 2② 由limlnx,limx 故此例属于x型，由罗比塔法则有： 

1

lnx1limalimxlim0(a0,x0) xxxaxa1xaxa

14、利用泰勒公式

对于求某些不定式的极限来说，应用泰勒公式比使用罗比塔法则更为方便，下列为常用的展开式：

x2xn

o(xn) 1、e1x2!n!x

x3x5x2n1

n12、sinxx(1)o(x2n) 3!5!(2n1)!

2nx2x4

nx3、cosx1(1)o(x2n1) 2!4!(2n)!

nx2

n1x(1)o(xn) 4、ln(1x)x2n

5、(1x)1x

6、(1)2!x2(1)(n1)n!xno(xn) 1 1xx2xno(xn) 1x

n上述展开式中的符号o(x)都有:

o(xn)limn0 x0x

例:求limx0a2xax(a0) x

解:利用泰勒公式，当x0 有

10

x1

于是 limx0xo(x) 2a2xax x

2xx)aa xa(=limx0

1x12xa1()o(x)1o(x)2a2a =limx0x

a

=limx01xxo(x)o(x)12a2a limx0xx2a

15、利用拉格朗日中值定理

定理:若函数f满足如下条件：

(I) f 在闭区间上连续

(II)f 在(a ,b)内可导

则在(a ,b)内至少存在一点,使得

f'()

此式变形可为: f(b)f(a) baf(b)f(a)f'(a(ba)) (01) ba

exesinx

例: 求 lim x0xsinx

解:令f(x)e 对它应用中值定理得 x

exesinxf(x)f(sinx)(xsinx)f'(sinx(xsinx)) (01)即: exesinx

f'(sinx(xsinx)) (01) xsinx

11

f'(x)ex连续

limf'(sinx(xsinx))f'(0)1 x0

exesinx

1 从而有: limx0xsinx

16、求代数函数的极限方法

(1)有理式的情况，即若:

P(x)a0xma1xm1amR(x)(a00,b00) nn1Q(x)b0xb1xbn

(I)当x时，有

a0mnb0mm1a0xa1xamP(x)limlim0 mn xQ(x)xbxnbxn1b01n mn

(II)当x0 时有:

①若Q(x0)0 则 limP(x)P(x0) x0Q(x)Q(x0)

P(x) x0Q(x)②若Q(x0)0 而 P(x0)0 则lim

③若Q(x0)0,P(x0)0,则分别考虑若x0为P(x)0的s重根,即:P(x)(xx0)sP1(x) 也为Q(x)0的r重根,即: Q(x)(xx0)rQ1(x) 可得结论如下：

0 , sr(xx0)srP1(x)P1(x0)P(x)limlim, sr xx0Q(x)xx0Q1(x)Q1(x0) ,sr 

例：求下列函数的极限

12

x33x2(2x3)20(3x2)30

①lim ②lim4 x1x4x3x(2x1)50

解: ①分子，分母的最高次方相同，故 330(2x3)20(3x2)30220330

() lim=5050x22(2x1)

②P(x)x33x2,P(1)0

Q(x)x44x3,Q(1)0

P(x),Q(x)必含有（x-1）之因子，即有1的重根 故有:

x33x2(x1)2(x2)x21 lim4limlimx1x4x3x1(x1)2(x22x3)x1x22x32

(2)无理式的情况。虽然无理式情况不同于有理式，但求极限方法完全类同，这里就不再一一详述.在这里我主要举例说明有理化的方法求极限。

例：求lim(xxxxx)

xxx) 解: lim(xx

limxxxx

xxxx

xx

xxxx

1

x

113x12 xlimxlimx1x

二、多种方法的综合运用

上述介绍了求解极限的基本方法，然而，每一道题目并非只有一种方法。因此我们在解题中要注意各种方法的综合运用的技巧，使得计算大为简化。

13

lim1cosx2

例:求 0x2sinx2

x[解法一]:

1cosx2limx0x2

sinx2

2xsinx2sinx2

limx02xx2cosx22xsinx2 limx0x2cosx2sinx2 sinx2

lim21x02=cosx2

sinx

2 x2

注:此法采用罗比塔法则配合使用两个重要极限法。

解法二]:

2

2

x2x2lim1cosx2sinsinx2

x0x2sinx2=limx0x2sinx2limx0x21sin

sinx2

x2

12 2x2

2

2注：此解法利用“三角和差化积法”配合使用两个重要极限法。

[解法三]:

lim1cosx21cosx22xsinx22xsinx21x0x2sinx2limx0x2x2limx04x3limx04xx

22 注:此解法利用了两个重要极限法配合使用无穷小代换法以及罗比塔法则

[解法四]:

(x2)2

lim1cosx21cosx2x2x21x0x2sinx2limx0x4sinx2limx0x4sinx22

注:此解法利用了无穷小代换法配合使用两个重要极限的方法。

14

[

[解法五]:

x2x2

2142

lim1cosx22sin2()xx0xsinx2limx0x2sinx2limx0x2(x2)limx0x4122

注:此解法利用“三角和差化积法”配合使用无穷小代换法。

[解法六]：

令ux2

lim1cosx21cosusinu

x0x2sinx2limu0usinulimu0sinuucosu

limcosu1 u0cosucosuusinu2

注：此解法利用变量代换法配合使用罗比塔法则。

[解法七]:

1cosx2sinx2

lim11x0x2sinx2limx0x2cosx2sinx2limx0x2

12

tgx2

注:此解法利用了罗比塔法则配合使用两个重要极限。

(作者: 黄文羊)

15

爱华网本文地址 » http://www.aihuau.com/a/382451/732744921606.html