相关解答一:什么是圆曲线的主点,圆曲线的曲线要素有哪些
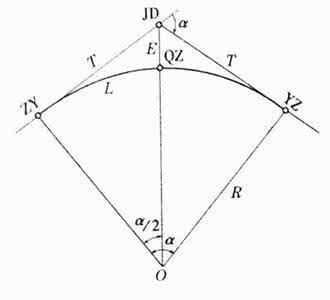
线路工程测量中,什么是圆曲线元素?圆曲线主点用什么符号表示?代表什么意义? - - - 圆曲线的曲线要素有:半径R、转角θ、曲线长L、切线长T、外距E、切曲差q,主点桩号. 主点的符号有:直圆点ZY,表示路线由直线进入圆曲线的点 曲中点QZ,表示圆曲线的中点 圆直点YZ,表示路线由圆曲线进入直线的点
相关解答二:道路工程中平曲线要素里面有两个曲线长:圆曲线长 和平曲线长。
圆曲线长度指YH点到HY点的长度,平曲线长是不是指的ZY点与YZ点之间的长度包含圆曲线长和缓和曲线长度
相关解答三:圆曲线与缓曲线的区别
圆曲线(圆曲线段长度)【circular curve】指的是道路平面走向改变方向或竖向改变坡度时所设置的连接两相邻直线段的圆弧形曲线。圆曲线的分类 由一个圆曲线组成的曲线称为单曲线;由两个或两个以上同向圆曲线组成的曲线称为复曲线。转向相同的两相邻曲线连同其间的直线段所组成的曲线称为同向曲线;转向相反的两相邻曲线连同其间的紶线段所组成的曲线称为反向曲线。 缓和曲线【transition curve】指的是平面线形中,在直线与圆曲线,圆曲线与圆曲线之间设置的曲率连续变化的曲线。缓和曲线是道路平面线形要素之一,它是设置在直线与圆曲线之间或半径相差较大的两个转向相同的圆曲线之间的一种曲率连续变化的曲线。《公路工程技术标准》(JTG B01-2003)规定,除四级路可不设缓和曲线外,其余各级公路都应设置缓和曲线。在现代高速公路上,有时缓和曲线所占的比例超过了直线和圆曲线,成为平面线形的主要组成部分。在城市道路上,缓和曲线也被广泛地使用。 L乘以π 由于直线与圆曲线间存在曲率半径的突变,圆曲线半径越大,这种突变程度就越小。当圆曲线半径超过2000m时,这种突变对轨道交通行车影响很小。而当正线上曲线半径不大于2000m时,则要在圆曲线与直线间加设缓和曲线,实现曲率半径的逐渐过渡,减少列车在突变点处的轮轨冲击。因此,《地铁设计规范》(GB50157—2003)规定:“线路平面圆曲线与直线之间应根据曲线半径、超高设置及设计速度等因素设置缓和曲线,其长度可按表的规定采用。”
相关解答四:什么是缓和曲线,与圆曲线有何不同。
缓和曲线为缓和汽车转弯时的离心力,使其顺适、自然、和谐、均匀、舒适地完成转向行驶,需在直线与圆曲线间或是半径不同的两个圆曲线之间设置缓和曲线。缓和曲线的半径是不断变化的,即曲率从零渐变到某一定值,符合汽车行驶的自然轨迹。缓和曲线形式多样,如回旋曲线、三次抛物线、双纽线、多心复曲线。其中,回旋曲线应用广泛,现代高等级公路上普遍采用回旋曲线。按计算行车速度,各级公路最小缓和曲线长度如下表所示。各级公路最小缓和曲线长度表公路等级 汽车专用路 一般公路高速公路 一 二 二 三 四地形 平原微丘 重丘 山岭平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘最小缓和曲线长度(m) 100 85 70 50 85 50 70 35 70 35 50 25 35 20注:四级公路为超高、加宽缓和段长度。为保障行车安全,平面线形应满足以下条件平面线形应直捷、连续、均衡,并与地形、地物相适应,与周围环境相协调。各级公路不论转角大小均应铺设曲线,并尽量选用较大的圆曲线半径。公路转角过小时,应设法调整平面线形,当不得已而设置小于70的转角时,则必须设置足够长的直线。两同向曲线间应设有足够长度的直线,不应以短直线相连。否则应调整线形使之成为一个单曲线或复曲线。两反向曲线间夹有直线段时,以不设置小于最小直线长度的直线段为宜,否则应调整线形或运用回旋线组合成S形曲线。三、四级公路两相邻反向曲线无超高、加宽时可径相衔接;无超高有加宽时,中间应设有长度不小于10m的加宽缓和段。曲线线形应特别注意技术指标的均衡与连续性。应避免连续急弯的线形,可在曲线间插入足够长的直线或回旋线。
相关解答五:什么是缓和曲线,与圆曲线有何不同。
缓和曲线为缓和汽车转弯时的离心力,使其顺适、自然、和谐、均匀、舒适地完成转向行驶,需在直线与圆曲线间或是半径不同的两个圆曲线之间设置缓和曲线。缓和曲线的半径是不断变化的,即曲率从零渐变到某一定值,符合汽车行驶的自然轨迹。
缓和曲线形式多样,如回旋曲线、三次抛物线、双纽线、多心复曲线。其中,回旋曲线应用广泛,现代高等级公路上普遍采用回旋曲线。
按计算行车速度,各级公路最小缓和曲线长度如下表所示。
各级公路最小缓和曲线长度表
公路等级 汽车专用路 一般公路
高速公路 一 二 二 三 四
地形 平原微丘 重丘 山岭平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘 平原微丘 山岭重丘
最小缓和曲线长度(m) 100 85 70 50 85 50 70 35 70 35 50 25 35 20
注:四级公路为超高、加宽缓和段长度。
为保障行车安全,平面线形应满足以下条件
平面线形应直捷、连续、均衡,并与地形、地物相适应,与周围环境相协调。
各级公路不论转角大小均应铺设曲线,并尽量选用较大的圆曲线半径。公路转角过小时,应设法调整平面线形,当不得已而设置小于70的转角时,则必须设置足够长的直线。
两同向曲线间应设有足够长度的直线,不应以短直线相连。否则应调整线形使之成为一个单曲线或复曲线。
两反向曲线间夹有直线段时,以不设置小于最小直线长度的直线段为宜,否则应调整线形或运用回旋线组合成S形曲线。三、四级公路两相邻反向曲线无超高、加宽时可径相衔接;无超高有加宽时,中间应设有长度不小于10m的加宽缓和段。
曲线线形应特别注意技术指标的均衡与连续性。
应避免连续急弯的线形,可在曲线间插入足够长的直线或回旋线。
相关解答六:曲线要素的分类
曲线要素广泛应用于道路桥梁设计、施工测量中。 曲线要素又分为平曲线要素、竖曲线要素。
相关解答七:缓和曲线的曲线要素
实地放样缓和曲线之前,需要计算若干曲线要素: 不同类型的缓和曲线,数值不同 不同类型的缓和曲线,数值不同 不同类型的缓和曲线,数值不同 上面的公式中 ——路线偏转角,单位:弧度。这是设计数据;R——圆曲线半径,单位:m。这是设计数据;——缓和曲线偏转角,单位:弧度;p——内移距,单位:m;q——切线增长,单位:m;(有些文献用 m 表示该变量)T——切线长,单位:m;E——外距,单位:m;D——切曲差,即切线长减去曲线长,单位:m;注意:的计算公式请见下文,每种类型的缓和曲线都有自己的计算公式。[式中 α 为路线设计参数,R值对于设计道路可查相关规范]
相关解答八:线路工程测量中,什么是圆曲线元素
线路工程测量中,什么是圆曲线元素?圆曲线主点用什么符号表示?代表什么意义?
-
-
-
圆曲线的曲线要素有:半径R、转角θ、曲线长L、切线长T、外距E、切曲差q,主点桩号.
主点的符号有:直圆点ZY,表示路线由直线进入圆曲线的点
曲中点QZ,表示圆曲线的中点
圆直点YZ,表示路线由圆曲线进入直线的点
相关解答九:如何学好圆锥曲线
解析几何学习方法专题
抓住基础 数形结合
“数缺形时少直观,形少数时难入微,数形结合百般好,隔裂分家万事休.”——我国著名数学家华罗庚
作为学习解析几何的开始,我们引入了我国著名的数学家华罗庚的一句话,他告诉了我们“数”和“形”各自的特点和不足,从而强调了数形结合的重要性,尤其是在解析几何的学习过程中,我们始终都要注意运用数形结合的思想和方法。
当然,学习这一部分内容,只是了解这种思想也是不够的,现在,就为大家介绍一下学习解析几何的方法和需要注意的几点。
基础也很重要
几种圆锥曲线的定义你能说得出吗?
很多同学对上面的这个问题可能会不屑一顾,但是,你能完整的回答出来吗?
以椭圆的定义为例,我们引入椭圆的时候,是用了怎样的定义?之后,我们是不是又给了椭圆一个第二定义呢?椭圆的第二定义又是以什么为基础呢?对于所有的圆锥曲线,我们是不是又有一个统一的定义呢?三种重要的圆锥曲线,又各有怎样的性质,你能说出它们的异同点吗?
这些问题,你都能回答出来吗?
★定义不是用来背的
有些同学可能现在就会去翻书,去查定义,会说,回答这些问题还不容易嘛,我背一下不就可以了吗。可是,我要告诉大家——定义不是用来背的。
可能大家还没有理解这句话的意思,定义不是要你去死记硬背,而是要你去自己理解,去自己总结。
教材上引入椭圆定义的时候花费了很大的篇幅,可它的本质是什么?与双曲线的定义又有怎样的相同点、不同点?椭圆、双曲线和抛物线这三个重要的圆锥曲线的统一定义我们又该如何去理解?这些,只有靠你自己总结出来,才能真正成为你自己的东西,在做题的时候,你才能应用自如。看一遍书上的定义,合上课本,想一想,如果让你来描述,你会怎么说。当你能够给别人将这些定义解释清楚的时候,你就已经很好的理解了这些定义,做题时,你就不会因为忽略了定义中隐含的条件而一筹莫展了。
★比一比 学会总结
这一章我们介绍了三种圆锥曲线,它们有很多的相似之处,当然也有很多的不同,它们之间也有着千丝万缕的联系。学习完之后,自己比较一下,它们的定义、性质都有什么异同,哪些量是它们共有的,哪些量是某个圆锥曲线所特有的。当你比较完之后,再回过头来看这一章,你会发现,原来这一章的内容竟然如此的简单和清晰。
记住,一定要自己去总结哦!!别人给你的东西永远都是别人的,不是你自己的,只有自己总结过,才能清晰的把握问题的重点。
“数”与“形”紧密联系
我们掌握了圆锥曲线的基础之后,就好比为我们的大厦打下了一个坚实的基础,现在,我们就可以正式建造我们的摩天大楼了!
★让“数”直观
如我们开始引言中所讲“数缺形时少直观”,我们如何让“数”变得直观呢?
给你 ,你会说这是一个等式,是一个二元二次方程。
给你 ,你会说这是一个方程组,一个二元一次的方程组。
如果我们把(x,y)看作是平面上的一点,你看到上面的式子又会想到什么呢?
是不是我们的圆锥曲线的一种? 和 是不是平面内的两条直线,而 所决定的(x,y)是不是两条直线的交点?
可能通过上面的例子,你还看不出让“数”直观的重要性。那我们再举一个例子:已知 ,求 的最小值。如果你不能让“数”直观,那么这是一道非常复杂的计算题。但是,看到这样的两个式子,你又能想到怎样的“形”呢? 很明显是一个圆,而我们要求的最小值呢?你能不能想到,它其实是一个两点距离的平方,要求它的最小,也就是求动点P(x,y)和定点A(3,-3)之间距离的最小,而这里的x,y需要满足 ,也就是说点P一定要在这样的一个圆上,求......余下全文>>
相关解答十:单圆曲线是什么
由一个圆曲线组成的曲线称为单曲线;由两个或两个以上同向圆曲线组成的曲线称为复曲线。转向相同的两相邻曲线连同其间的直线段所组成的曲线称为同向曲线;转向相反的两相邻曲线连同其间的直线段所组成的曲线称为反向曲线。
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网