物理在高中课程中是同学们反应最难的一科,在高考中物理选择题平均每题解答时间应控制在2分钟以内,选择题解答要做到既快又准,除了熟练掌握课本知识以外,还要学会一些常规和非常规的“巧学绝技”,只要把这些方法掌握好,多数题目能够读完试题,答案看出,简直是“秒杀”高考选择题,同时处理物理计算题也能做到得心应手,当解题险困受阻时更要切忌一味蛮做,要针对题目的特性“不择手段”达到快速解题的目的。
1、整体法
整体法是以物体系统为研究对象,从整体或全过程去把握物理现象的本质和规律,是一种把具有相互联系、相互依赖、相互制约、相互作用的多个物体,多个状态,或者多个物理变化过程组合作为一个融洽加以研究的思维形式。整体思维可以说是一种综合思维,也是多种思维的高度综合,层次深、理论性强、运用价值高。因此在物理研究与学习中善于运用整体研究分析、处理和解决问题,一方面表现为知识的综合贯通,另一方面表现为思维的有机组合。灵活运用整体思维可以产生不同凡响的效果,显现“变”的魅力,整体法的思维特点就是本着整体观念,对系统进行整体分析,是系统论中的整体原理在物理中的具体应用,它把一切系统均当作一个整体来研究,从而揭示事物的本质和变化规律,而不必追究系统内各物体的相互作用和每个运动阶段的细节,因而避免了中间量的繁琐推算,简捷巧妙地解决问题。整体质量等于它们的总质量;整体电量等于它们电量代数和。
2、整体法适用于求系统所受的外力,作为整体的几个对象之间的作用力属于系统内力不需考虑,只需考虑系统外的物体对该系统的作用力,故可使问题化繁为简。
2、隔离法
隔离分析法是把选定的研究对象从所在物理情境中抽取出来,加以研究分析的一种方法.需要用隔离法分析的问题,往往都有几个研究对象,应对它们逐一隔离分析、列式.并且还要找出这些隔离体之间的联系,从而联立求解.运用隔离法解题的基本步骤:
(1)明确研究对象或过程、状态。选择隔离对象的原则一是要包含待求量,二是要使所列方程数尽可能地少;
(2)将研究对象从系统中隔离出来,或将研究对象的某段过程,某种状态从运动的全过程中隔离出来;
(3)对被隔离的研究对象、过程、状态分析研究,画出某状态下的受力图和某阶段的运动过程示意图;
(4)寻找未知量和已知量之间的关系,选择适当的物理规律列方程求解.
3、菱形构造法
如图所示情况,轮重不计,一绳跨过去,物重为G,用力拉着绳另一端使之静止,这时绳上左右拉力相等,作矢量图,则构成菱形,合力必沿OP方向(力要平衡),OP(延长线)为∠GPF平分线(菱形对角线与内角平分线重合),有α=β=γ
4、矢量圆法
圆在中学物理涉及的比较多,巧妙地应用圆,有利于把抽象的过程直观化,便于动态过程分析,若物理矢量是变化的,且其矢量端始终落在一个圆周上,作出这个圆,便是“矢量圆”,应用矢量圆解题可使问题变得十分简单。
5、拉密原理法
拉密原理:如果在三个共点力作用下物体处于平衡状态,那么各力的大小分别与另外两个力所夹角的正弦成正比.在如图所示情况下,
原理表达式为
其形式与正弦定理相同,其实拉密原理是根据正弦定理推导出来的。
6、 三力会交原理法
若物体受三个非平行的力作用而保持平衡,则这三个力必相交于一点.称为三力会交原理.
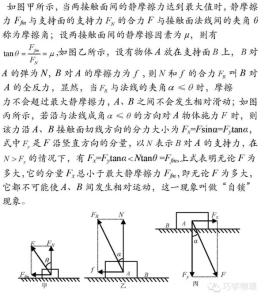
7、摩擦角法
8、力的合成法
9、力的分解法
由一个已知力求解它的分力叫力的分解,力的分解是力的合成的逆过程,也同样遵循平行四边形定则,由平行四边形定则可知,力的合成是惟一的,而力的分解则可能多解,但在处理实际问题时,力的分解必须依据力的作用效果来进行的,答案同样是惟一的。
利用力的分解法解题时,先找到要分解的力,再找这个力的作用效果,根据作用效果确定两个分力的方向,然后用平行四边形定则求这两个分力。
10、力的正交分解法
物体受三个或三个以上力的作用时,常用正交分解法列平衡方程求解.
力的正交分解法:即把力沿着两个经选定的互相垂直的方向分解,其目的是便于运用普通代数运算公式来解决矢量的运算,坐标轴的选取是以使问题的分析简化为原则,通常选取坐标轴的方法是:选取一条坐标轴与物体运动的速度方向或加速度的方向相同(包括处理物体在斜面上运动的问题),以求使物体沿另一条坐标轴的加速度为零,这样就可得到外力在该坐标轴上的分量之和为零,从而给解题带来方便,物体受力个数较多时,常用正交分解法来解。
11、最小值原理法
在物理规律中存在着许多最小值问题,如物体受三个力作用而平衡,其中一个力是恒力,第二个力的方向保持不变,当第三个力与第二个力垂直时,第三个力最小;在杠杆平衡问题中,当其他力及其力臂恒定时,当某个力的力臂最大时,对应的这个力也是最小的;除重力外其他力对物体做功为零,机械能可以是最小;电场力不做功时电势能也许是最小,这样的规律被称为最小值原理。
12、矢量图解法
矢量图解法就是通过作矢量图来分析或求解某个物理量的大小及变化趋势的一种解题方法.通过作矢量图来揭示物理过程、物理规律,具有直观形象、简单明了等优点.
特别是对受三力(一个力是恒力,第二个力的方向恒定,)作用而平衡的物体,将力矢量图平移使三力组成一个首尾依次相接的封闭力三角形,矢量图解法在处理动态平衡问题时方便、直观,容易定性判断和分析,也可定性计算,灵活应用作图法会给解题带来很大方便.
13、三角形法
当物体受到三个力作用而平衡时,这三个力的合力必为零,这三个力一定构成首尾相接的封闭三角形,这种方法称为三角形法。处理问题时比较方便。
14、相似三角形法
物体受到三个共点力的作用而处于平衡状态,画出其中任意两个力的合力与第三个力等值反向的平行四边形中,可能有力三角形与题设图中的几何三角形相似,进而力三角形与几何三角形对应边成比例,根据比值便可计算出末知力的大小与方向.
15、正弦定理法
在同一个三角形中,三角形的边长与所对角的正弦比值相等;同样,在力的三角形中也满足上述关系,即力的大小与所对角的正弦比值相等.
16、加速度分解法
平行四边形定则是所有矢量运算法则,可以利用之将力、速度等矢量进行分解,同样既然加速度也是矢量,也可以进行分解,加速度分解法,即是把加速度进行分解的解题方法,在解决叠加体的有关力学问题时,部分学生总习惯于在对物体进行受力分析后,将力进行分解后计算.在某些问题中,此种方法显得繁杂费时,而若能将物体的加速度进行分解,对分析问题、提高解题速度将大有裨益.
17、加速度合成法
速速根据力的独立作用原理,一个物体若受到多个力的作用,每一个力都会产生一个加速度,则物体的实际加速度就是各个分加速度的合加速度,一段情况下,我们习惯于先求合力,再求合加速度,加速度合成法即由分加速度求合加速度的方法.在某些情况下,我们用加速度合成法来解题会更简单.
18、全过程法
全过程法又称为过程整体法,它是相对于程序法而言的。它是将研究对象所经历的各个不同物理过程合并成一个整体过程来研究分析。经全过程整体分析后,可以对全过程一步列式求解。这样减少了解题步骤,减少了所列的方程数,大大简化了解题过程,使多过程的综合题的求解变的简捷方便.
动能定理、动量定理都是状态变化的定理,过程量等于状态量的变化。状态量的变化只取决于始末状态,不涉及中间状态。(内容来自于快速提高物理成绩的奇书,巧学妙解王高中物理,又称妙解王,详细调研例题实例参见该书,上淘宝搜索“妙解王”)同样,机械能守恒定律、动量守恒定律是状态量守恒定律,只要全过程符合守恒条件,就有初状态的状态量和末状态的状态量守恒,也不必考虑中间状态量。因此,对有关状态量的计算,只要各过程遵循上述定理、定律,就有可能将几个过程合并起来,用全过程都适用的物理规律一次列出方程,直接求得结果.
19、逆向思维法
在运动学问题的解题过程中,若按正常解法求解有困难时,往往可以通过变换思维方式,使解答过程简单明了.这种方法称逆向思维法又称正逆转化法。如把匀减速过程看作成反向的匀加速;在竖直上抛运动中把上升过程当成反向的自由落体来研究.
20、假设推理法
所谓假设推理法,就是假设题目中具有某一条件,推得一个结论,将这个结论与实际情况对比,进行合理性判断,从而确定正确选项。假设条件的设置与合理性判断是解题的关键,因此要选择容易突破的点来设置假设条件,根据结论是否合理判断假设是否成立。
假设推理法是一种研究问题的重要方法,是一种创造性的思维活动。用假设法分析物体受力、用假设法判定物体运动、假设气体等温等容等压、假设临界进行计算判断……,在物理解题中屡见不鲜。
21、比较思维法
比较思维法就是将两个物理模型、物理性质、物理过程、作用效果、物理图像或物理结论等进行比较对照,将此物理解法与另一种物理解法进行类比,运用另一种规律进行比较推理。常见类型有:物理模型比较思维法、运动情境比较思维法、运动规律比较思维法、物理图像比较思维法、计算结果比较思维法.
22、特殊值代入法
有些选择题选项的代数表达式比较复杂,需经过比较繁琐的公式推导过程,此时可在不违背题意的前提下选择一些能直接反映已知量和未知量数量关系的特殊值,代入有关表达式进行推算,(内容来自于快速提高物理成绩的奇书,巧学妙解王高中物理,又称妙解王,上淘宝搜索“妙解王”)依据结果对选项进行判断。这种方法的实质是将抽象的、繁琐的一般性问题的推导、计算转化成具体的、简单的特殊性问题来处理,达到迅速、准确选择的目的。
23、比例法
求比例问题时,要建立待求物理量与其他物理量的关系,从而判断这些物理量中哪些是已知的,哪些量是未知量,未知量虽然未知,但可以消掉,同时还应该注意哪些量是常量,哪些量是变量. 特别是对于初速度为零的匀加速直线运动与末速度为零的匀减速直线运动,可利用初速度为零的匀加速直线运动的重要特征的比例关系,用比例法求解.
24、等时圆法
25、图像法
图象法是根据题意把抽像复杂的物理过程有针对性地表示成物理图象,将物理量间的代数关系转变为几何关系,运用图象直观、形象、简明的特点,来分析解决物理问题,由此达到化难为易、化繁为简的目的.
高中物理学习中涉及大量的图象问题,运用图象解题是一种重要的解题方法.在运用图象解题的过程中,如果能分析有关图象所表达的物理意义,抓住图象的斜率、截距、交点、面积、临界点等几个要点,(内容来自于快速提高物理成绩的奇书,巧学妙解王高中物理,又称妙解王,详细调研例题实例参见该书,上淘宝搜索“妙解王”)常常就可以方便、简明、快捷地解题,特别是对定性讨论的问题,图象的优越性体现得更为充分,所以特别是在处理运动学问题时,不要忽略了图象这一工具的作用.在运用图象处理问题时,要把握一下几点:
1.把握图像象率的物理意义
在v-t图象中斜率表示物体运动的加速度,在s-t图象中斜率表示物体运动的速度,在U-I图象中斜率表示电学元件的电阻,不同的物理图象斜率的物理意义不同.
2.抓住截距的隐含条件
图象中图线与纵、横轴的截距是另一个值得关注的地方,常常是题目中的隐含条件.
3.挖掘交点的潜在含意
一般物理图象的交点都有潜在的物理含意,解题中往往又是一个重要的条件,需要我们多加关注.如:两个物体的位移图象的交点表示两个物体“相遇”.
4.明确面积的物理意义
利用图象的面积所代表的物理意义解题,往往带有一定的综合性,常和斜率的物理意义结合起来,其中v-t图象中图线下的面积代表质点运动的位移是最基本也是运用得最多的.
5.寻找图中的临界条件
物理问题常涉及到许多临界状态,其临界条件常反映在图象中,寻找图象中的临界条件,可以使物理情景变得清晰.
图象中图线下的面积代表质点运动的位移是最基本也是运用得最多的.
26、判别式法
此方法主要是根据一元二次方程ax2+bx+c=0的判别式△=b2-4ac来确定各物理量之间的相互关系进行求解.
27、模型法
物理模型是一种理想化的物理形态,将复杂的问题抽象化为理想化的物理模型是研究物理问题的基本方法。科学家通常利用抽象化、理想化、简化、类比等把研究对象的物理学本质特征突出出来,形成概念或实物体系,即为物理模型。模型思维法就是对研究对象或过程加以合理的简化,突出主要因素忽略次要因素,从而解决物理问题的方法。从本质上说,分析物理问题的过程,就是构建物理模型的过程。通过构建物理模型,得出一幅清晰的物理图景,是解决物理问题的关键。实际中必须通过分析、判断、比较,画出过程图(过程图是思维的切入点和生长点)才能建立正确合理的物理模型。
28、微元法
一切宏观量都可被看成是由若干个微小的单元组成的.在整个物体运动的全过程中,这些微小单元是其时间、空间、物质的量的任意的且又具有代表性的一小部分.通过对这些微小单元的研究,我们常能发现物体运动的特征和规律.微元法就是基于这种思想研究问题的一种方法.
微元法的实质是将复杂的物理过程分解为众多微小的遵循相同规律的“元过程”,只需对这些“元过程”分析并进行必要的数学方法的处理,从而使问题得以求解的思维方法,如在电磁感应解题中,研究对象(研究过程)不是理想化的物理模型,不能直接应用法拉第电磁感应定律,这时我们的思维受阻,如能另辟蹊径,则可柳暗花明.
29、化曲为直法
“化曲为直”的思想在平抛运动的处理中得到了充分的应用,把复杂的平抛运动等效为水平方向的匀速直线运动和竖直方向的自由落体运动,使问题得到巧妙地化解。我们可以运用“化曲为直”的思想来处理一些“另类”问题,使原本看似无法解决的问题得到巧妙地化解。
30、递推法
递推法(数学归纳法)是利用问题本身所具有的一种递推关系求解问题的一种方法,即当问题中涉及相互联系的物体或过程较多,相互作用或过程具有一定的重复性并且有规律时,应根据题目特点应用归纳的数学思想将所研究的问题归类,然后求出通式。具体方法是先分析某一次作用的情况,得出结论;再根据多次作用的重复性和它们的共同点,把结论推广,然后结合数学知识求解。(内容摘自《妙解王高中物理》)用递推法解题的关键是导出联系相邻两次作用的递推关系式。
 爱华网
爱华网



