浓度问题——基础学习
一、 解答题
3、求混合之前的初始状态例1:现有一种预防甲型H1N1流感的药物配制成的甲、乙两种浓度不同的消毒液。若从甲中取2100克,乙中取700克混合而成的消毒溶液的浓度为3%,若从甲中取900克,乙中取2700克,则混合而成的消毒溶液的浓度为5%,则甲、乙两种消毒溶液的浓度分别为( )。
A.3%,6% B.3%,4% C.2%,6% D.4%,6%
【答案】C
【解题关键点】设甲、乙两种溶液溶液浓度分别是x,y,则2100x+700y=(2100+700)×3%,900x+2700y=(900+2700)×5%,解得x=2%,y=6%。
【结束】
4、求混合之前的初始状态例2:取甲种硫酸300克和乙种硫酸250克,再加水200克,可混合成浓度为50%的硫酸;而取甲种硫酸200克和乙种硫酸150克,再加上纯硫酸200克,克混合成浓度为80%的硫酸。那么甲、乙两种硫酸的浓度各是多少?( )
A.75%,60% B.68%,63% C.71%,73% D.59%,65%
【答案】A
【解题关键点】设甲、乙硫酸浓度分别是x、y,则300x+250y=(300+250+200)×50%,200x+150y+200=(200+150+200)×80%,解得x=75%,y=60%。
【结束】
6、求混合后的最终状态例1:130克含盐5%的盐水,含盐9%的盐水混合,配成含盐6.4%的盐水,这样配成的6.4%的盐水有多少克( )
A.120 B.180 C.200 D.300
【答案】C
【解题关键点】设配成的盐水有x克,则可列方程130×5%+(x-130)×9%=x×6.4%,解得x=200。
【结束】
8、增加溶剂(稀释问题)例1:有浓度为60%的溶液若干,加了一定数量的水后,稀释成48%的溶液,如果再加入同样多的水,浓度是多少?( )
A.40% B.45% C.50% D.55%
【答案】A
【解题关键点】设原有溶液a克,加入水x克,最后浓度为y,60%a=48%(a+x)=y(a+2x)。解得y=40%。
【结束】
10、减少溶剂(蒸发问题)例1:13000千克青菜,早晨测得它的含水率为97%,这些菜到了下午测得含水率为95%,那么这些菜的重量减少了( )千克。
A. 200 B.300 C.400 D.500
【答案】C
【解题关键点】青菜中除了水之外的其他成分质量不会变化,下午含水率为95%的菜重量为1000×(1—97%)÷(1-95%)=600千克,所以青菜重量减少了1000-600=400千克,选择C。
【结束】
11、减少溶剂(蒸发问题)例2:有浓度为4%的盐水若干千克,蒸发了一些水分后浓度变成10%,再加入300克40%的盐水后,浓度变为6.4%的盐水,问最初的盐水多少克?( )
A. 200 B.300 C.400 D.500
【答案】D
【解题关键点】首先,根据题意,可以用十字交叉法确定与300克4%的盐水混合得到浓度为6.4%盐水的10%浓度盐水的重量为200克。再设最初盐水x克,则200×10%=x×4%,可得x=500克。
【结束】
12、推导法(按题意从初始状态逐步计算直至最终状态)例1:一满杯水溶有10克糖,搅匀后喝去;添入6克糖,加满水搅匀,再喝去;添入6克糖,再加满水搅匀,又喝去;再添入6克糖,加满水搅匀,仍喝去。问:此时杯中所剩的糖水中有多少克糖?( )
A. B. C. D.5
【答案】A
【解题关键点】初始杯中含有10克糖,喝完第一次后剩×10克糖,喝完第二次剩()×10克糖,喝完第三次剩()×10克糖,喝完第四次剩()×10=克。第二次加入的6克糖,喝完第一次后剩×6克糖,喝完第三次剩()×6克糖,喝完第四次后剩()×6=克糖,第三次加入的6克糖,喝完第三次后还剩×6克糖,喝完第四次后剩()×6=克糖。第四次加入的6克糖,当喝完第四次后还剩×6=2克糖。综上分析,最后杯中含糖+++2=3克糖。
【结束】
13、推导法(从最终状态逆推求出初始状态)例1:有浓度为4%的盐水若干千克,蒸发了一些水分后浓度变成10%,再加入300克40%的盐水后,浓度变为6.4%的盐水,问最初的盐水多少克?( )
A. 200 B.300 C.400 D.500
【答案】D
【解题关键点】首先,根据题意,可以用十字交叉法确定与300克4%的盐水混合得到浓度为6.4%盐水的10%浓度盐水的重量为200克。再设最初盐水x克,则200×10%=x×4%,可得x=500克。
【结束】
15、方程法例1:甲、乙两杯奶茶分别重300克和120克,甲中含奶茶粉120克,乙中含奶茶粉90克。从两杯中应各取出多少克才能兑成浓度为50%的奶茶140克?( )
A. 90,50 B.100,40 C.110,30 D.120,20
【答案】B
【解题关键点】可设取出甲x克,乙(140-x)克,那么,[x×+×(140-x)] ÷140=50%,解得x=100.所以取100克的甲,取140-100=40克的乙。
【结束】
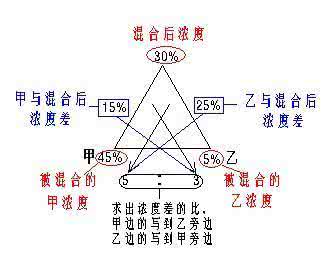
16、方程法例2:130克含盐5%的盐水,与含盐9%的盐水混合,配成含盐6.4%的盐水,这样配成的6.4%的盐水有多少克( )
A.120 B.180 C.200 D.300
【答案】C
【解题关键点】设配成的盐水有x克,则克列方程130×5%+(x-130)×9%=x×6.4%,解得x=200.
【结束】
18、十字交叉法例1:在浓度为75%的酒精中加入10千克水,浓度变为35%,再加入L千克纯酒精,浓度变为60%,则L为多少千克?( )
A.8 B.11.7 C.14.6 D.16.4
【答案】B
【解题关键点】十字交叉法。第一次混合相当于浓度为75%与0%的溶液混合。
75%的酒精 75% 35%
\ ∕
35%
∕ \
水 0% 40%
所以75%的酒精与水的比例为35:40=7:8。水10千克,75%的酒精8.75千克,混合后共18.7千克。第二次混合,相当于浓度为35%与100%的溶液混合。
35%的酒精 35% 40%
\ ∕
60%
∕ \
纯酒精 100% 25%
所以35%的酒精与纯酒精的比例为40:25=8:5,即18.75:L=8:5,L≈11.7千克。
【结束】
19、十字交叉法例2:把浓度为20%、40%和60%的某溶液混合在一起,得到浓度为36%的溶液50升。已知浓度为40%的溶液用量是浓度为20%的溶液用量的3倍。浓度为40%的溶液的用量是多少升?( )
A. 36 B.38 C.44 D.46
【答案】A
【解题关键点】设20%的溶液为x升,则40%的溶液为3x升,相当于(20%×x+40%×3x)÷4x=35%的溶液4x升与60%的溶液y升混合。用十字交叉法,则
所以4x:y=24:1,即x=6y。带入方程35%×4x+60y=36%×50,解得x=12,所以浓度为40%的溶液用了3x=36升。
【结束】
20、分析猜答案法:深刻理解混合的本质(公式的理解),分析题目才出答案;
21、分析猜答案法例1:现有一种预防禽流感药物配置成的甲、乙两种不同浓度的消毒溶液,若从甲中取2100克,乙中取700克混合而成的消毒溶液的浓度为3%;若甲种取900克,乙中取2700克,则混合而成的消毒溶液的浓度为5%,则甲、乙两种消毒溶液的浓度分别为( )
A. 3%,6% B.3%,4% C.2%,6% D.4%,6%
【答案】C
【解题关键点】首先可以根据溶质相等,构造方程。
方程法:设甲、乙溶液的浓度分别为x、y,则
通过解方程可以得到答案,但是此种方法会用掉比较多的时间,所以我们应该寻找更为简便的做法。
分析猜提法:题目中说一定量的甲溶液和一定量的乙溶液混合,得到3%溶液,则可以说明,甲、乙溶液浓度一种大于3%,一种小于3%。同理可得,甲、乙溶液浓度一种大于5%,另一种小于5%,综合得出甲、乙溶液一种大于5%,一种小于3%从选项可以看出,答案为C.
【结束】
 爱华网
爱华网