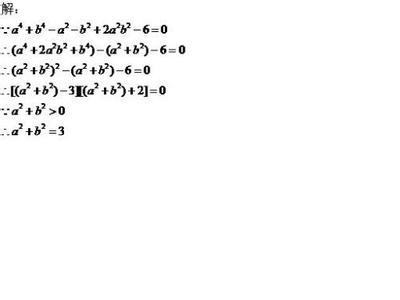实质上B2-4AC >0时情况可以作为一个通用公式,因为一般实数均可用复数形式表述。按下述方法可以简明地判断重根。
与三次方程不同的是,四次方程求解需要复数运算支持,因为中间数据均会出现复数。我已经发表的复数系统可作为计算的工具使用。关于四次方程求解程序我暂时无时间写,不过可利用QR方法求任意实数多项式方程的所有根(QR程序我也已发表于博客中,可以引用)。
一元四次方程一般式:ax4+bx3+cx2+dx+e=0(a≠0,a,b,c,d,e∈R)
p=-(3b2-8ac) q=3b4+16a2c2-16ab2c+16a2bd-64a3e
r=-(b3-4abc+a2d) 2
A=p2-3q B=pq-9r C=q2-3pr
若A=B=0
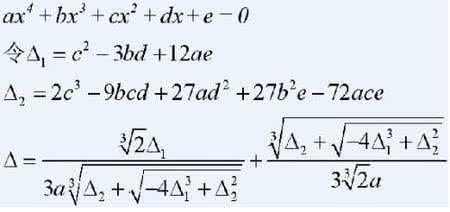
y1=y2=y3=-p/3=-q/p=-3r/q
x1=1/4a(-b+√y1+√y2+√y3) X3=1/4a(-b+√y1-√y2-√y3)
X2=1/4a(-b-√y1+√y2-√y3) X4=1/4a(-b-√y1-√y2+√y3)
若B2-4AC=0
y1=-p+k y2=y3=-k/2
k=B/A A<>0 ///新补充
x1=1/4a(-b+√y1+√y2+√y3) X3=1/4a(-b+√y1-√y2-√y3)
X2=1/4a(-b-√y1+√y2-√y3) X4=1/4a(-b-√y1-√y2+√y3)
若B2-4AC<0
T=(2Ap-3B)/(2A1.5 )
y1=-1/3(p+2Acos(1/3ArccosT))
y2=-1/3(p+2Acos(1/3ArccosT+2π/3))
y3=-1/3(p+2Acos(1/3ArccosT-2π/3))
x1=1/4a(-b+√y1+√y2+√y3)
X2=1/4a(-b-√y1+√y2-√y3)
X3=1/4a(-b+√y1-√y2-√y3)
X4=1/4a(-b-√y1-√y2+√y3)
若 B2-4AC >0
令
 爱华网
爱华网