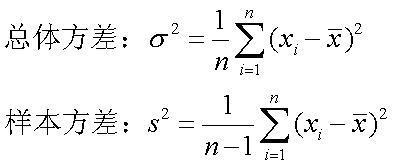一般地设n个数据,x1,x2,…xn的平均数为.x,
则方差S2=1n[(x1-.x)2+(x2-.x)2+…+(xn-.x)2,
它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.而标准差是方差的算术平方根,
同样也反映了数据的波动情况.
故选C.
考点:
考点名称:方差方差:是各个数据与平均数之差的平方和的平均数。
在概率论和数理统计中,方差用来度量随机变量和其数学期望(即均值)之间的偏离程度。
在许多实际问题中,研究随机变量和均值之间的偏离程度有着很重要的意义。
设有n个数据各数据x1,x2,…,xn各数据与它们的平均数的差的平方分别是,,…,,我们用它的平均数,即用来衡量这组数据的波动大小,并把它叫做这组数据的方差,记作。方差特点:
(1)设c是常数,则D(c)=0。
(2)设X是随机变量,c是常数,则有D(cX)=(c2)D(X)。
(3)设 X 与 Y 是两个随机变量,则
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的,当X,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),
则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况。
(4)D(X)=0的充分必要条件是X以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。
(5)D(aX+bY)=a^2DX+b^2DY+2abE{[X-E(X)][Y-E(Y)]}。
意义:
在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
标准差:
方差的算术平均根,即,并把它叫做这组数据的标准差,它也是一个用来衡量一组数据的波动大小的重要的量。
公式:
方差是实际值与期望值之差平方的期望值,而标准差是方差算术平方根。 在实际计算中,我们用以下公式计算方差。
方差是各个数据与平均数之差的平方的平均数,即s^2=(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2],其中,x_表示样本的平均数,n表示样本的数量,^,xn表示个体,而s^2就表示方差。
而当用(1/n)[(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]作为样本X的方差的估计时,发现其数学期望并不是X的方差,而是X方差的(n-1)/n倍,[1/(n-1)][(x1-x_)^2+(x2-x_)^2+...+(xn-x_)^2]的数学期望才是X的方差,用它作为X的方差的估计具有“无偏性”,所以我们总是用[1/(n-1)]∑(xi-X~)^2来估计X的方差,并且把它叫做“样本方差”。
方差,通俗点讲,就是和中心偏离的程度!用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)并把它叫做这组数据的方差。记作S².在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定。
方差分析主要用途:
①均数差别的显著性检验;
②分离各有关因素并估计其对总变异的作用;
③分析因素间的交互作用;
④方差齐性检验。
 爱华网
爱华网