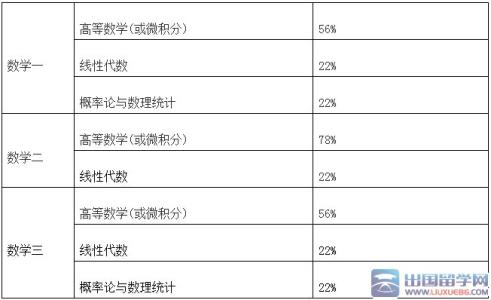
21.(本小题满分14分)
对于函数f(x)?ax2?(b?1)x?b?2(a?0),若存在实数x0,使f(x0)?x0成立,则称x0为f(x)的不动点.
⑴当a=2,b=-2时,求f(x)的不动点;
⑵若对于任何实数b,函数f(x)恒有两相异的不动点,求实数a的取值范围; ⑶在⑵的条件下,若y?f(x)的图象上A、B两点的横坐标是函数f(x)的不动点,且直线y?kx?
12a?1
2
是线段AB的垂直平分线,求实数b的取值范围.
2高三数学2单元测试卷(二)
第二单元 函数
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.设函数y?f(x)与函数g(x)的图象关于x?3对称,则g(x)的表达式为
A.g(x)?f(?x) C.g(x)?f(?3?x)
32
B.g(x)?f(3?x) D.g(x)?f(6?x)
2.设a?log0.34,b?log43,c?0.3?2,则a、b、c的大小关系是 A.a<b<c B.a<c<b C.c<b<a D.b<a<c 3.指数函数y=f(x)的反函数的图象过点(2,-1),则此指数函数为
A.y?()x
12
B.y?2x C.y?3x D.y?10x
4.已知函数f(x)??x?x3,x1、x2、x3?R,且x1?x2?0,x2?x3?0,x3?x1>0,
则f(x1)?f(x2)?f(x3)的值 A.一定大于零
B.一定小于零
C.等于零
D.正负都有可能
5.若函数f(x)?logax?在区间(-1,0)上有f(x)?0,则f(x)的递增区间是
A.(-∞,1)
B.(1,+∞)
C.(-∞,-1) D.(-1,+∞)
6.已知0?loga2?logb2,则a、b的关系是
A.0<a<b<1
B.0<b<a<1
x
C.b>a>1 D.a>b>1
7.已知0?a?1,则方程a
A.1个
?logax的实根个数是
B.2个 C.3个 D.1个或2个或3个
8.若logxy??2,则x?y的最小值为
32
A.
2
3
23B
3
3
33C
2
2D.
3
1-
9.已知函数f(x)是定义在R上的奇函数,当x<0时,f(x)=( )x,那么f 1(-9)的值为
3

A.2
B.-2
C.3
D.-3
10.若方程?x2?x?m无实数解,则实数m的取值范围是
A.(-∞,-1) B.[0,1)
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.函数f(x)?logax满足f(9)?2,则f
?1
C.2,+∞) D.(-∞,-1)∪2,+∞)
(?log92)的值是__________________.
12.使函数y?x2?4x?5具有反函数的一个条件是____________________________.
(只填上一个条件即可,不必考虑所有情形).
13.函数y?log1(x?2x)的单调递减区间是________________________.
2
2
14.已知f(x)是定义在R上的偶函数,并且f(x?2)??
则f(105.5)?_________________.
1
,当2?x?3时,f(x)?x,f(x)
x2?1
15.关于函数f(x)?lg(x?0,x?R)有下列命题:
|x|
①函数y?f(x)的图象关于y轴对称; ②在区间(??,0)上,函数y?f(x)是减函数; ③函数f(x)的最小值为lg2;
④在区间(1,?)上,函数f(x)是增函数. 其中正确命题序号为_______________.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
已知函数f(x)=ax+
x?2
(a>1) x?1
⑴证明:函数f(x)在(-1,+∞)上为增函数; ⑵用反证法证明f(x)=0没有负数根.
17.(本小题满分12分)
已知f(x)=2-1的反函数为f
-
x
?1
(x),g(x)=log4(3x+1).
⑴若f1(x)≤g(x),求x的取值范围D; 1
⑵设函数H(x)=g(x)-f2
?1
(x),当x∈D时,求函数H(x)的值域.
18.(本小题满分14分)
函数f(x)=loga(x-3a)(a>0,且a≠1),当点P(x,y)是函数y=f(x)图象上的点时, Q(x-2a,-y)是函数y=g(x)图象上的点. ⑴写出函数y=g(x)的解析式.
⑵当x∈[a+2,a+3]时,恒有|f(x)-g(x)|≤1,试确定a的取值范围.
2高三数学2单元测试卷(一)
第一单元 集合与简易逻辑
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.设集合P={3,4,5},Q={4,5,6,7},定义P※Q={(a,b)|a∈P,b∈Q},则P※Q
中元素的个数为 A.3 B.4 C.7 D.12 2.设A、B是两个集合,定义A-B={x|x∈A,且x?B},若M={x||x+1|≤2},N={x|x=|sinα|,
α∈R},则M-N= A.[-3,1]
B.[-3,0]
C.[0,1]
D.[-3,0]
3.映射f:A→B,如果满足集合B中的任意一个元素在A中都有原象,则称为―满射‖.已
知集合A中有4个元素,集合B中有3个元素,那么从A到B的不同满射的个数为 A.24
B.6
C. 36
D.72
4.若lga+lgb=0(其中a≠1,b≠1),则函数f(x)=ax与g(x)=bx的图象
A.关于直线y=x对称 C.关于y轴对称
B.关于x轴对称
D.关于原点对称
5.若任取x1、x2∈[a,b],且x1≠x2,都有f(
x1+x2
2f(x1)+f(x2)
)>成立,则称f(x) 是[a,b]上
2
的凸函数.试问:在下列图像中,是凸函数图像的为
A
6.若函数f(x)=x- +在(1,+∞)上是增函数,则实数p的取值范围是
x2
A.[-1,+∞)
B.[1,+∞)
C.(-∞,-1]
D.(-∞,1]
7.设函数f(x)=x|x|+bx+c,给出下列四个命题: ①c=0时,f(x)是奇函数 ③f(x)的图象关于(0,c)对称 其中正确的命题是
A.①④
B.①③
C.①②③
D.①②④
ex+1
8.函数y=,x∈(0,+∞)的反函数是
e-1
②b=0,c>0时,方程f(x)=0只有一个实根 ④方程f(x)=0至多两个实根
pp
A.y=x-1
x∈(-∞,1) x+1x+1
B.y=x∈(-∞,1)
x-1
x-1
C.y=x∈(1,+∞)
x+1x+1
D.y=,x∈(1,+∞)
x-1
9.如果命题P:??{?},命题Q:??{?},那么下列结论不正确的是 A.―P或Q‖为真
B.―P且Q‖为假
C.―非P‖为假
D.―非Q‖为假
10.函数y=x2-2x在区间[a,b]上的值域是[-1,3],则点(a,b)的轨迹是图中的 A.线段AB和线段AD C.线段AD和线段BC
答题卡
B.线段AB和线段CD D.线段AC和线段BD
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
11.已知函数f(x)是定义在(-3,3)上的奇函数,当0<x<3时,f(x)的
图象如图所示,则不等式f(x)cosx<0是 .
12.国家规定个人稿费纳税办法是:不超过800过800 元而不超过4000元的按超过800元部分的14%纳税;超过4000元的按全部稿
酬的11%纳税.已知某人出版一本书,共纳税420元时,这个人应得稿费(扣税前)为 元.
?x2,x?0,
13.已知函数f(x)=f(x)??若f(f(x0))?2,则x0= .
?2cosx,0?x??.
14.若对于任意a∈[-1,1],函数f(x)=x2+(a-4)x+4-2a的值恒大于零,则x的取值范
围是 . 15.如果函数f(x)的定义域为R,对于m,n∈R,恒有f(m+n)=f(m)+f(n)-6,且f(-1)是
不大于5的正整数,当x>-1时,f(x)>0.
那么具有这种性质的函数f(x)= .(注:填上你认为正确的一个函数即可) 三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
二次函数f(x)满足f (x+1)-f (x)=2x且f (0)=1. ⑴求f (x)的解析式;
⑵在区间[-1,1]上,y=f (x)的图象恒在y=2x+m的图象上方,试确定实数m的范围. 17.(本小题满分12分)
已知集合A={x|(x?2)[x?(3a?1)]?0},B={x|⑴当a=2时,求A?B; ⑵求使B?A的实数a的取值范围.
x?2a
?0}.
x?(a2?1)
18.(本小题满分14分)
22
已知命题p:方程ax?ax?2?0在[-1,1]上有解;命题q:只有一个实数x满足
不等式x?2ax?2a?0,若命题―p或q‖是假命题,求实数a的取值范围.
2
19.(本小题满分14分)
设函数f(x)?2x?a?2?x?1(a为实数).
⑴若a<0,用函数单调性定义证明:y?f(x)在(??,??)上是增函数;
⑵若a=0,y?g(x)的图象与y?f(x)的图象关于直线y=x对称,求函数y?g(x) 的解析式.
20.(本小题满分14分)
函数f(x)?2x?
a
的定义域为(0,1](a为实数). x
⑴当a??1时,求函数y?f(x)的值域;
⑵若函数y?f(x)在定义域上是减函数,求a的取值范围;
⑶求函数y?f(x)在x∈(0,1]上的最大值及最小值,并求出函数取最值时x的值.
19.(本小题满分14分)
某化妆品生产企业为了占有更多的市场份额,拟在2005年度进行一系列促销活动,经过市场调查和测算,化妆品的年销量x万件与年促销t万元之间满足3-x与t+1成反比例,如果不搞促销活动,化妆品的年销量只能是1万件,已知2005年生产化妆品的设备折旧,维修等固定费用为3万元,每生产1万件化妆品需再投入32万元的生产费用,若将每件化妆品的售价定为:其生产成本的150%“与平均每件促销费的一半”之和,则当年生产的化妆品正好能销完.
⑴将2005年的利润y(万元)表示为促销费t(万元)的函数;
⑵该企业2005年的促销费投入多少万元时,企业的年利润最大?
(注:利润=销售收入—生产成本—促销费,生产成本=固定费用+生产费用)
20.(本小题满分14分)
已知f(x)在(-1,1)上有定义,f(
x?y1
)=-1,且满足x,y∈(-1,1)有f(x)+f(y)=f() 21?xy
⑴证明:f(x)在(-1,1)上为奇函数; ⑵对数列x1=
2xn1
,xn+1=,求f(xn); 221?xn
⑶求证
1112n?5
??????
f(x1)f(x2)f(xn)n?2
21.(本小题满分14分)
对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点.如果函数 f(x)=ax2+bx+1(a>0)有两个相异的不动点x1,x2.
⑴若x1<1<x2,且f(x)的图象关于直线x=m对称,求证:⑵若|x1|<2且|x1-x2|=2,求b的取值范围.
1
<m<1; 2
2高三数学2单元测试卷(三)
第三单元 数列
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
81524
1.数列-1,,?错误!未定义书签。的一个通项公式是
579
n3+n
A.an=(-1)
2n+1
n
B.an=(-1)n D.an=(-1)n
n(n+3)
2n+1n(n+2)
2n+1
C.an=(-1)
2
n (n+1)-1
2n-1
2.设Sn是等差数列{an}的前n项和,已知S6=36,Sn=324,Sn-6=144,则n=
A.15
B.16
C.17
D.18
3.在等比数列{an}中,S4=1,S8=3,则a17+a18+a19+a20的值是
A.14 B.16 C.18
D.20
4.已知-9,a1,a2,-1四个实数成等差数列,-9,b1,b2,b3,-1五个实数成等比数
列,则b2(a2-a1)=
9
A.8 B.-8 C.±8 D.8
5.设等差数列{an}的前n项的和为Sn,若a1>0,S4=S8,则当Sn取得最大值时,n的值为 A.5 B.6 C.7 D.8
n+1
6.已知数列{an}的通项公式an=log2n∈N+),设其前n项和为Sn,则使Sn<-5成立的
n+2
正整数n
A.有最小值63 B.有最大值63 C.有最小值31 D.有最大值31
7.设数列{an}是公比为a(a≠1),首项为b的等比数列,Sn是前n项和,对任意的n∈N+ ,
点(Sn ,Sn+1)在
A.直线y=ax-b上 B.直线y=bx+a上 C.直线y=bx-a上 D.直线y=ax+b上
8.数列{an}中,a1=1,Sn是前n项和,当n≥2 时,an=3Sn,则limSn?1的值是
n??Sn?1?3
A.-2
4B
5
1
C D.1
3
9.北京市为成功举办2008年奥运会,决定从2003年到2007年五年间更新市内现有的全部出租车,若每年更新的车辆数比前一年递增10%,则2003年底更新现有总车辆数(参考数据1.14=1.46,1.15=1.61)
A.10% B.16.5% C.16.8% D.20%
10.已知a1,a2,a3,?,a8为各项都大于零的数列,则“a1+a8<a4+a5”是“a1,a2,a3,?,a8不是等比数列”的
A.充分且必要条件 B.充分但非必要条件 C.必要但非充分条件 D.既不充分也不必要条件
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
n ?).我们把使乘积a2a2a2?2a为整数的数n叫做? 11.已知 a n ? log n ? 1 ( 2 )( n ? N 123n
“劣数”,则在区间(1,2004)内的所有劣数的和为 .
12.已知集合An?{x|2n?x?2n?1,且x?7m?1,m,n?N?},则A6中各元素的和为 . 13.等差数列{an}中,a1=-5,它的前11项的平均值是5,若从中抽取1项,余下10项的平均值是4,则抽取的是第 项.
14.若a+b+c,b+c-a,c+a-b,a+b-c依次成等比数列,公比为q,则q3+q2+q
= .
15.若数列{an}(n?N?)为等差数列,则数列bn?
a1?a2?a3???an
(n?N?)
n
也为等差数列,类比上述性质,相应地,若数列{cn}是等比数列且cn?0(n?N?),则有数列dn= (n∈N+)也是等比数列.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
已知等差数列{an}的首项a1=1,公差d>0,且第二项,第五项,第十四项分别是等比数列{bn}的第二项,第三项,第四项. ⑴求数列{an}与{bn}的通项公式.
⑵设数列{cn}对任意正整数n,均有c2004的值.
17.(本小题满分12分)
cc1c2c3
??????n?an?1,求c1+c2+c3+?+b1b2b3bn
3
已知f(x+1)=x2-4,等差数列{an}中,a1=f(x-1),a2=- ,a3=f(x).求:
2⑴x的值;
⑵数列{an}的通项公式an; ⑶a2+a5+a8+?+a26. 18.(本小题满分14分)
正数数列{an}的前n项和为Sn,且2Sn=an+1.
(1) 试求数列{an}的通项公式;
11
(2)设bn={bn}的前n项和为Tn,求证:Tn<
2an2an+1
19.(本小题满分14分)
1
已知函数f(x)定义在区间(-1,1)上,f(=-1,且当x,y∈(-1,1)时,恒有
2x-y12a111
f(x)-f(y)=f(,又数列{an}满足a1=an+1设bn=+. ,21+anf(a1)f(a2)f(an)1-xy⑴证明:f(x)在(-1,1)上为奇函数; ⑵求f(an)的表达式;
⑶是否存在正整数m,使得对任意n∈N,都有bn<值;若不存在,请说明理由.
20.(2005年湖南理科高考题14分)
自然状态下的鱼类是一种可再生资源,为持续利用这一资源,需从宏观上考察其再生能
*
力及捕捞强度对鱼群总量的影响.用xn表示某鱼群在第n年年初的总量,n∈N,且x1>0.不考虑其它因素,设在第n年内鱼群的繁殖量及捕捞量都与xn成正比,死亡量与xn2成正比,这些比例系数依次为正常数a,b,c. ⑴求xn+1与xn的关系式;
⑵猜测:当且仅当x1,a,b,c满足什么条件时,每年年初鱼群的总量保持不变?(不要求证明)
*
⑶设a=2,c=1,为保证对任意x1∈(0,2),都有xn>0,n∈N,则捕捞强度b的最大允许值是多少?证明你的结论.
m-8
成立,若存在,求出m的最小4
21.(本小题满分14分)
已知函数f(t)满足对任意实数x,y都有f(x+y)=f(x)+f(y)+xy+1,且f(-2)= -2. ⑴求f(1)的值;
⑵证明:对一切大于1的正整数t,恒有f(t)>t; ⑶试求满足f(t)=t的整数t的个数,并说明理由.
2高三数学2单元测试卷(四)
第四单元 [三角函数]通,性质大集中
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.(2005年全国高考题)函数f (x) = | sin x+cos x |的最小正周期是
ππA B. C.π
422.若cos??0,且sin2??0,则角?的终边所在象限是
A.第一象限
B.第二象限
C.第三象限
D.2π
D.第四象限
3.若函数f(x)?sin(?x??)的图象(部分)如图所示,则?和?的取值是
A.??1,??
?
3
B.??1,???
?
3
1?
C.??,??
261?
D.??,???
26
4.函数y?2sin(
A. [0,
?
6
?2x)(x?[0,?])为增函数的区间是
B. [
?] 3
?
12
,
7?] 12
C. [
?
3
,
5?] 6
D. [
5?
,?] 6
5.定义在R上的函数f(x)既是偶函数又是周期函数.若f(x)的最小正周期是?,且当
21A. ?
2x?[0,
?
]时,f(x)?sinx,则f(
B.
5?
)的值为 3
C. ?
1 2 2
D.
3 2
6.(2005年全国高考题)锐角三角形的内角A、B 满足tan A-
A.sin 2A –cos B = 0 C.sin 2A – sin B = 0
1
= tan B,则有
sin2A
B.sin 2A + cos B = 0 D.sin2A+sinB=0
?
7.为了得到函数y?sin(2x?)的图象,可以将函数y?cos2x的图象
6
π
A.向右平移个单位长度
6π
C
6
π
B
3π
D.向左平移 3
πcos2x
8.当0<x<4时,函数f(x) ( )
cosxsinx-sinxA.4
B.
12
C.2
π
π
D.
14
9.(2005年全国高考题)已知函数y =tan?x在(-2,2( )
A.0 <?≤1 B.-1 ≤?< 0 C.?≥ 1 D.?≤ -1 10.设y?f(t)是某港口水的深度y(米)关于时间t(时)的函数,其中0?t?24.下
象.下面的函数中,最能近似表示表中数据间对应关系的函数是(t?[0,24])( ) A.y?12?3sinC.y?12?3sin
?
6
t t
B.y?12?3sin(
?
6
t??)
?
12
D. y?12?3sin(
?
12
t?
?
2
)
二、填空题:本大题共5小题,每小题4分(15小题每空2分),共20分.把答案填在横线
上.
sin3α13
11.(2005年全国高考题)设α为第四象限的角,若,则tan2α =_____________. sinα5
12.(2005年上海春季高考题)函数y?sinx?arcsinx的值域是
nππ
13.设f(n)=cos( 2+4),则f(1)+f(2)+?+f(2006)=.
14.已知tanα+cotα=-2,则tanα+cotα=
15.(2005年湖南高考题)函数y=f(x)的图象与直线x=a,x=b及x轴所围成图形的面积
π2
称为函数f(x)在[a,b]上的面积.已知函数y=sinnx在[0,]上的面积为(n∈N*),则
nn
2π
(i)函数y=sin3x在[0]上的面积为 ;
3π4π
(ii) 函数y=sin(3x-π)+1在[,上的面积为
33
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
n
n
16.(本题满分12分)
??1??2
已知sin(?2?)?sin(?2?)?,??(,),求2sin??tan??cot??1的值.
44442
17.(本题满分12分)(2005年上海春季高考题)
已知tanα是方程x2?2xsec??1?0的两个根中较小的根,求?的值.
18.(本题满分14分) (2005年湖南高考题)
已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0.求角A、B、C的大小.
19.(本题满分14分)(2005年广东高考题)
6k -1π6k +1
化简f(x)=cos(π+2x)+cos(-2x)+3sin(x)(x∈R,k∈Z),并求函数
333f(x)的值域和最小正周期.
20.(本题满分14分)(2005年天津高考题)
某人在一山坡P处观看对面山项上的一座铁塔,如图所示,塔高BC=80(米),塔所在的山高OB=220(米),OA=200(米),图中所示的山坡可视为直线l且点P在直线l1
上,l与水平地面的夹角为α,tanα=,试问此人距水平地面多高时,观看塔的视角∠
2BPC最大(不计此人的身高)
21.(本题满分14分)
设关于x的函数y?2cos2x?2acosx?(2a?1)的最小值为f(a). ⑴ 写出f(a)的表达式; ⑵试确定能使f(a)?
1
的a值,并求出此时函数y的最大值. 2
2高三数学2单元测试卷(五)
第五单元 [向量]作运算,图形见奇观
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.(2005年全国Ⅱ高考题)已知点A(3,1),B(0,0),C(3,0).设∠BAC的平分线AE
→=λCE→,其中λ等于 与BC相交于E,那么有BC
A.2
11B. C.-3 D.-
23
→OB→=OB·→OC→=OC·→OA→,则O点一定是△ABC的 2.已知O是△ABC内一点,且满足OA·
A.内心 B.外心 C.垂心 D.重心
????????3.在四边形ABCD中,AB?a?2b,其中a、b不共线,BC??4a?b,CD??5a?3b,
则四边形ABCD是 A.梯形 B.矩形
C.菱形
D.正方形
?????????????????????4.在边长为1的正△ABC中,若AB?a,BC?b,CA?c,则a·b+b·c+c·a=
3 A
2
3B
2
C.3
D.0
5.已知,,为非零的平面向量. 甲:???,乙:?,则甲是乙的( ) A.充分条件但不是必要条件 C.充要条件
B.必要条件但不是充分条件 D.非充分条件非必要条件
3
,则这个三角2
6.已知三角形的三条边成公差为2的等差数列,且它的最大角的正弦值为形的面积是 15 A
4
3 B.
4
21C
4
35D.4
??x
7.把点(3,4)按向量a平移后的坐标为(-2,1),则y=2的图象按向量a平移后的图象的
函数表达式为
--++
A.y=2x5+3 B.y=2x5-3 C.y=2x5+3 D.y=2x5-3 8.(2005年全国Ⅱ高考题)点P在平面上作匀数直线运动,速度向量v=(4,-3)(即点P的运动方向与v相同,且每秒移动的距离为|v|个单位).设开始时点P的坐标为(-10,10),则5秒后点P的坐标为 A.(-2,4) B.(-30,25) C.(10,-5) D.(5,-10)
????????????????????9.已知向量OB=(2,0),OC=(2,2),CA=(cosα,sinα)( α∈R),则OA与OB
夹角的取值范围是
A.[0,
p4
B.[,
p45p12]
C.[
p5p1212
D.[
5pp12,2]
10.在△ABC中,a=x,b=2,B=45°,若这样的△ABC有两个,则实数x的取值范围是 A.(2,+∞)
B.(0,2)
C.(2,2
答题卡
D.(2,2)
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
11.(2005年湖南高考题)已知直线ax+by+c=0与圆O:x2+y2=1相交于A、B两点,且|AB|
????????
=3,则OA2OB= .
12.(2005年全国Ⅰ高考题)△ABC的外接圆的圆心为O,两条边上的高的交点为H,
OH?m(OA?OB?OC),则实数m = .
13.(2005年天津高考题)在直角坐标系xOy中,已知点A(0,1)和点B(-3,4),若点C在∠AOB的平分线上且|OC|=2,则OC= .
????????????
14.(2005年全国Ⅲ高考题)已知向量OA?(k,12),OB?(4,5),OC?(?k,10),且A、B、C
三点共线,则k= .
???
15.设a、b、c是任意的非零平面向量,且相互不共线,则
???????①(a?b)?c?(c?a)?b?0;
????②a?b?a?b;
???????
③(b?c)a?(c?a)b不与c垂直;
?2???2??
④(3a?2b)?(3a?2b)=9a?4b中是真命题的有
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分l2分)
如图,在Rt△ABC中,已知BC=a,若长为2a的线段PQ以点A为中点,问PQ与BC 的夹角?取何值时BP?CQ的值最大?并求出这个最大值.
P
17.(本题满分12分)
??AA
A、B、C为△ABC的三内角,且其对边分别为a、b、c.若m=(-cossin,
22????1AA
n=(cos2,sin2),且m2n=2
(1)求A;
(2)若a=23,三角形面积S3,求b+c的值.
18.(本题满分14分)
如图,△AOE和△BOE都是边长为1的等边三角形,延长OB到C使|BC|=t(t>0),连AC交BE于D点.
????????
⑴用t表示向量OC和OD的坐标;
????????
⑵(理)求向量OD和EC的夹角的大小.
????3????????????
(文)当OC=OB时,求向量OD和EC的夹角的大小.
2
19.(本题满分14分)
??
已知a?(cos?,sin?),b?(cos?,sin?)(0??????). ????
⑴求证:a?b与a?b互相垂直;
????
⑵若ka?b与a?kb大小相等,求???(其中k为非零实数).
20.(本题满分14分)
设△ABC的外心为O,以线段OA、OB为邻边作平行四边形,第四个顶点为D,再以OC、OD为邻边作平行四边形,它的第四个顶点为H.
??????
⑴若OA?a,用a、b、c表示OH; OB?b,OC?c,
⑵求证:AH⊥BC;
→. ⑶设△ABC中,∠A=60°,∠B=45°,外接圆半径为R,用R表示|OH|
21.(本题满分14分)
已知圆O的半径为R,它的内接△ABC中,2R(sin2A?sin2C)?(2a?b)sinB成立,求三角形ABC面积S的最大值.
2高三数学2单元测试卷(六)
第三单元 [不等]符号定,比较技巧深
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.不等式(1+x)(1-|x|)>0的解集是 A.{x|0≤x<1} C.{x|-1<x<1}
B.{x|x<0且x≠-1} D.{x|x<1且x≠-1}
2 2
2.直角三角形ABC的斜边AB=2,内切圆半径为r,则r的最大值是 A2
B.1
C
D2-1
3.(2005年天津高考题)给出下列三个命题 ①若a?b??1,则
ab
? 1?a1?b
②若正整数m和n满足m?n,则m(n?m)?
2
2
n 2
③设P(x1,y1)为圆O1:x?y?9上任一点,圆O2以Q(a,b)为圆心且半径为1. 当(a?x1)?(b?y1)?1时,圆O1与圆O2相切 其中假命题的个数为 A.0
B.1
C.2
D.3
2
2
4.不等式|2x-log2x|<2x+|log2x|的解集为 A.(1,2) B.(0,1)
C.(1,+∞) D.(2,+∞)
5.如果x,y是实数,那么―xy<0‖是―|x-y|=|x|+|y|‖的
A.充分条件但不是必要条件 B.必要条件但不是充分条件
C.充要条件 D.非充分条件非必要条件
ln2ln3ln5
6.(2005年全国Ⅲ高考题)若a=b=c=
235 A.a<b<c
B.c<b<a
C.c<a<b
D.b<a<c
7.已知a、b、c满足c?b?a,且ac?0,那么下列选项中不一定成立的是 A.ab?ac B.c(b?a)?0 C.cb?ab D.ac(a?c)?0 8.(2005年全国Ⅰ高考题) 设0?a?1,函数f(x)?loga(a2x?2ax?2),则使f(x)?0 的x的取值范围是 A.(-∞,0)
B.(0,+∞)
C.(-∞,loga3)
D.(loga3,+∞)
2
2
9.某工厂第一年年产量为A,第二年的增长率为a,第三年的增长率为b,这两年的平均增长率为x,则 A.x=
a?b
2
B.x≤
a?ba?ba?b
C.x> D.x≥ 222
10.设方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q,函数f(x)=(x+p)(x+q)+2,则
A.f(2)=f(0)<f(3)
B.f(0)<f(2)<f(3)
C.f(3)<f(0)=f(2)
D.f(0)<f(3)<f(2)
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 1x2?ax
12x+a-1
11.对于-1<a<1,使不等式()<()成立的x的取值范围是_______ .
2212.(2005年全国Ⅰ高考题)若正整数m满足1013.已知f(x)?
m?1
?2512?10m,则m = .(lg2≈0.3010)
?
1,x?0,
则不等式x?(x?2)?f(x?2)≤5的解集是 .
?1,x?0,
2
b2
?1,则. 14.已知a>0,b>0,且a?2
15.对于0?a?1,给出下列四个不等式 ①loga(1?a)?loga(1?
1?a
1?1a
1) a
②loga(1?a)?loga(1?
1?a
1?1a
1) a
?a ?a ③a ④a
其中成立的是
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分l2分) (2005年全国Ⅱ高考题)
设函数f(x)?2
|x?1|?|x?1|
,求使f(x)≥22的x取值范围.
17.(本题满分12分)(2005年全国Ⅲ高考题)
已知函数f(x)?2sin2x?sin2x,x?[0,2?].求使f(x)为正值的x的集合.
18.(本题满分14分)
a2b2(a?b)2
⑴已知a,b是正常数,a?b,x,y?(0,??),求证:,指出等号成??
xyx?y
立的条件;
⑵利用⑴的结论求函数f(x)?值.
19.(本题满分14分)
291
?x?(0,))的最小值,指出取最小值时x 的x1?2x2
设函数f(x)=|x-m|-mx,其中m为常数且m<0. ⑴解关于x的不等式f(x)<0;
⑵试探求f(x)存在最小值的充要条件,并求出相应的最小值.
20.(本题满分14分)
已知a>0,函数f(x)=ax-bx.
⑴当b>0时,若对任意x∈R都有f(x)?1,证明a?2;
⑵当b>1时,证明对任意x?[0,1],都有|f(x)|?1的充要条件是b-1?a?2; ⑶当0<b?1时,讨论:对任意x?[0,1],都有|f(x)|?1的充要条件.
2
21.(本题满分14分) (2005年全国Ⅰ高考题)
⑴设函数f(x)?xlog2x?(1?x)log2(1?x) (0?x?1),求f(x)的最小值; ⑵设正数p1,p2,p3,?,p2n满足p1?p2?p3???p2n?1,证明 p1log2p1?p2log2p2?p3log2p3???p2nlog2p2n??n.
2高三数学2单元测试卷(七)
第三单元 直线与圆
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知θ∈R,则直线xsin??y?1?0的倾斜角的取值范围是
A.[0°,30°]
B.[150°,180°) D.[30°,150°]
C.[0°,30°]∪[150°,180°)
2.已知两点M(-2,0),N(2,0),点P满足PM?PN=12,则点P的轨迹方程为
x2
A.y2=1
16C.y2-x2=8
B.x2+y2=16 D.x2+y2=8
3.已知两点P(4,-9),Q(-2,3),则直线PQ与y轴的交点分所成的比为
1
A.3
2
1B.
2
2
2
C.2 D.3
4.M(x0,y0)为圆x?y?a(a?0)内异于圆心的一点,则直线x0x?y0y?a2与该圆的位置关系为
A.相切
B.相交
C.相离
D.相切或相交
5.已知实数x,y满足2x?y?5?0,那么x2?y2的最小值为
A.5
B.
C.5
D.10
6.已知点P(3,2)与点Q(1,4)关于直线l对称,则直线l的方程为
A.x-y+1=0
2
B.x-y=0 C.x+y+1=0 D.x+y=0
7.已知a?b,且asin?+acos?-
??2
=0 ,bsin?+bcos?-=0,则连接(a,a2),
44
C.相离
D.不能确定
(b,b2)两点的直线与单位圆的位置关系是 A.相交
B.相切
8.直线l1:x+3y-7=0、l2:kx- y-2=0与x轴、y轴的正半轴所围成的四边形有外接圆,则
k 的值等于
A.-3 B.3 C.-6 D.6
9.在如图所示的坐标平面的可行域(阴影部分且包括边 界)内,目标函数z?2x?ay取得最大值的最优解有无 数个,则a为
A.-2
B.2
C.-6
D.6
10.设△ABC的一个顶点是A(3,-1),∠B,∠C的平分线方程分别是x=0,y=x,则
直线BC的方程是
A.y=2x+5
B.y=2x+3
C.y=3x+5 D.y??
x5
?
22
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.三边均为整数且最大边的长为11的三角形的个数为.
12.已知圆C的方程为x2?y2?r2,定点M(x0,y0),直线l:x0x?y0y?r2有如下两组
论断:
第Ⅰ组 第Ⅱ组
(a) 点M在圆C内且M不为圆心 (1) 直线l与圆C相切 (b) 点M在圆C上 (2) 直线l与圆C相交 (c )点M在圆C外 (3) 直线l与圆C相离
由第Ⅰ组论断作为条件,第Ⅱ组论断作为结论,写出所有可能成立的命题 . (将命题用序号写成形如p?q的形式)
?x?3y?3?0
y?2?
13.已知x、y满足?x?0,,则z=的取值范围是 .
x?1?y?0
?
14.已知A(-4,0),B(2,0)以AB为直径的圆与y轴的负半轴交于C,则过C点的
圆的切线方程为 .
15.过直线x?2上一点M向圆?x?5???y?1??1作切线,则M到切点的最小距离为
.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
自点(-3,3)发出的光线L射到x轴上,被x轴反射,其反射线所在直线与圆
2
2
x2?y2?4x?4y?7?0相切,求光线L所在直线方程.
17.(本小题满分12分)
某厂准备生产甲、乙两种适销产品,每件销售收入分别为3千元,2千元。甲、乙产品都需要在A,B两种设备上加工,在每台A,B上加工一件甲产品所需工时分别为1时、2时,加工一件乙产品所需工时分别为2时、1时,A,B两种设备每月有效使用台时数分别为400和500。如何安排生产可使收入最大?
18.(本小题满分14分)
设有半径为3km的圆形村落,A、B两人同时从村落中心出发,B向北直行,A先向东直行,出村后不久,改变前进方向,沿着与村落周界相切的直线前进,后来恰与B相遇.设A、B两人速度一定,其速度比为3:1,问两人在何处相遇?
19.(本小题满分14分)
已知圆(x+4)2+y2=25的圆心为M1,圆(x-4)2+y2=1的圆心为M2,一动圆与这两个圆都外切.
⑴求动圆圆心P的轨迹方程;
⑵若过点M2的直线与⑴中所求轨迹有两个交点A、B,求|AM1|2|BM1|的取值范围.
20.(本小题满分14分)
在平面直角坐标系中,在y轴的正半轴上给定A、B两点,在x轴正半轴上求一点C,使∠ACB取得最大值.
21.(本小题满分14分)
如图9-3,已知:射线OA为y=kx(k>0,x>0),射线OB为y= -kx(x>0),动点P(x,y)在∠AOx的内部,PM⊥OA于M,PN⊥OB于N,四边形ONPM的面积恰为k. (1)当k为定值时,动点P的纵坐标y是横坐标x的函数,求这个函数y=f(x)的解析式; (2)根据k的取值范围,确定y=f(x)的定义域.
2高三数学2单元测试卷(八)
第八单元 圆锥曲线
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
x2y2
1.已知双曲线2?2?1(a?0,b?0)的实轴长、虚轴长、焦距长成等差数列,则双曲线
ab
的离心率e为
45
A.2 B.3 C. D.
33
x2y2
??1的两个顶点,双曲线的两条准线经过椭圆的2.已知双曲线的两个焦点是椭圆
10064
两个焦点,则此双曲线的方程是
x2y2x2y2x2y2x2y2
??1 B.??1 C.??1 D.??1 A.
6030504060405030
x2y2
??1上的一点,则P到一条准线的距离与P到相应焦点的距离之3.已知P是椭圆
916
比为
4574A. B C. D.
5444.若抛物线y2=2px(p>0)上一点到准线和抛物线的对称轴的距离分别为10和6,则该点横坐标为
A.10 B.9 C.8 D.6
22
5.已知动点P(x,y)满足5(x?1)?(y?2)?|3x?4y?12|,则P点的轨迹是
A.两条相交直线 B.抛物线 C.双曲线 D.椭圆
1
6.过抛物线y2= - x的焦点F的直线交抛物线于A、B两点,且A、B在直线x4影分别M,N,则∠MFN等于
A.45° B.60° C.90° D.以上都不对 7.直线y=kx+2与双曲线x2-y2=6的右支交于不同两点,则k的取值范围是 A.(-C.(-
1515, 33
B.(015
) 3
1515,0) D.(,-1) 33
8.已知直线l交椭圆4x2+5y2=80于M、N两点,B是椭圆与y轴正半轴的交点,若△BMN
的重心恰好为椭圆的右焦点,则直线l的方程是
A.5x+6y-28=0 B.5x-6y-28=0 C.6x+5y-28=0 D.6x-5y-28=0
9.若动点P(x,y)与两定点M(-a,0),N(a,0)连线的斜率之积为常数k(ka≠0),则P点的轨迹一定不可能是
A.除M、N两点外的圆 B.除M、N两点外的椭圆 C.除M、N两点外的双曲线 D.除M、N两点外的抛物线 10.点(x,y)在曲线?
?x??2?cos?y
(?为参数,0????)上,则 x
?y?sin?
A.[-
33333] B.[-0) C.[-0] D.(-∞,33333
答题卡
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
(x?2)2y2
?2?1(a?0,b?0)的一条准线被它的两条渐近线截得线段的长度等11.双曲线2
ab
于它的一个焦点到一条渐近线的距离,则双曲线的两条渐近线的夹角为 .
12.双曲线 的两个焦点F1,F2,点P在双曲线上,若PF1⊥PF2,则点P到x
轴的距离为 .
x2y2
13.已知F1、F2是椭圆2?2?1(a?b?0)的焦点,P是椭圆上一点,且∠F1PF2=90°,
ab
则椭圆的离心率e的取值范围是 .
x2y2
14.椭圆C1:2?2?1(a?b?0)在第一象限部分的一点P,以P点横坐标作为长轴长,
ab
纵坐标作为短轴长作椭圆C2,如果C2的离心率等于C1的离心率,则P点坐标
为 .
15.设P是双曲线y2=4(x-1)上的一个动点,则点P到点(0,1)的距离与点P到y轴的
距离之和的最小值是 .
三、解答题(本大题共6小题,共80分) 16.(本小题满分12分)
x2y2π
??1的右焦点F作倾斜角为4A、B两点,求线段过双曲线
916
AB的中点C到焦点F的距离.
17.(本小题满分12分)已知双曲线x2-3y2=3的右焦点为F,右准线为l,以F为左焦点,
以l为左准线的椭圆C的中心为A,又A点关于直线y=2x的对称点A’恰好在双曲线的左准线上,求椭圆的方程.
18.(本小题满分14分)
如图所示,在直角梯形ABCD中,|AD|=3,|AB|=4,|BC|=3 ,曲线段DE上任一点
到A、B两点的距离之和都相等.
(1)建立适当的直角坐标系,求曲线段DE的方程; (2)过C能否作一条直线与曲线段DE相交,且所
得弦以C为中点,如果能,求该弦所在的直线 的方程;若不能,说明理由.
19.(本小题满分14分)
已知H(-3,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满
足?PM?0,PM??
3
. 2
⑴当点P在y轴上移动时,求点M的轨迹C;
⑵过点T(-1,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点E(x0,0),使
得△ABE是等边三角形,求x0的值.
20.(本小题满分14分)
x2y2
如图,椭圆2?2?1上的点M与椭圆右焦点F1的连线MF1与x轴垂直,且OM(O
ab
是坐标原点)与椭圆长轴和短轴端点的连线AB平行.
(1)求椭圆的离心率;
π
(2)F2是椭圆的左焦点,C是椭圆上的任一点,证明:∠F1CF2≤ ;
2(3)过F1且与AB垂直的直线交椭圆于P、Q,
若△PF2Q的面积是3 ,求此时椭圆的方程.
21.(本小题满分14分)
设x,y∈R,i,j为直角坐标平面内x,y轴正方向上的单位向量,若向量a=xi+(y+2)j,b=xi+(y-2)j,且|a|+|b|=8. (1)求点M(x,y)的轨迹C的方程;
(2)过点(0,3)作直线l与曲线C交于A、B两点,设??,是否存在这样
的直线l,使得四边形OAPB为矩形?若存在,求出直线l的方程;若不存在,试说明理由.
2高三数学2单元测试卷(九)
第九单元 [简单几何体],交角与距离
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的. 1.(2005年全国Ⅰ高考题)过三棱柱任意两个顶点的直线共15条,其中异面直线有
A.18对
面积为
B.24对 C.30对 D.36对
2..(2005年全国Ⅰ高考题)一个与球心距离为1的平面截球所得的圆面面积为?,则球的表
A.82? B.8? C.42? D.4?
3.设三棱柱ABC-A1B1C1的体积为V,P、Q分别是侧棱AA1、CC1上的点,且PA=QC1,则四棱锥B-APQC的体积为
VA.
6
VB.
4
VC.
3
VD.2
4.(2005年全国Ⅰ高考题)如图,在多面体ABCDEF中,已知ABCD是边长为1的正方形,且△ADE、△BCF均为正三角形,EF∥AB,EF=2,则该多面体的体积为
A.C.
2
3
4
3
B.
3 3
3D.2B.????m,???,??? D.n??,n??,m??
5.设α、β、γ为平面,m、n、l为直线,则m??的一个充分条件是
A.???,????l,m?l C.???,???,m??
6.如图,正方体ABCD-A1B1C1D1的棱长为1,O是底面A1B1C1D的中心,则O到平面ABC1D1的距离为 12
A. B.
24C.
2 2
D3 2
7.不共面的四个定点到平面?的距离都相等,这样的平面?共有
A.3个
B.4个
C.6个
D.7个
8.正方体ABCD-A1B1C1D1中,E、F分别为棱AB、C1D1的中点,则直线A1B1与平面A1ECF
所成角的正弦为 A.
6
3
B.
3 3
C.
6 6
D2 2
9.在空间直角坐标系O—xyz中,有一个平面多边形,它在xOy平面的正射影的面积为8,
在yOz平面和zOx平面的正射影的面积都为6,则这个多边形的面积为
A.246
B46
C.34
D34
10.将半径都为1的4个钢球完全装入形状为正四面体的容器里,这个正四面体的高的最小值为
A.
?26
3
B.2+
26
3
C.4+答题卡
26
3
D.
43?2
3
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.正三棱锥P-ABC的四个顶点同在一个半径为2的球面上,若正三 棱锥的侧棱长为23,则正三棱锥的底面边长是_____________ . 12.如图,PA⊥平面ABC,∠ABC=90°且PA=AB=BC=a, 则异面直线PB与AC所成角的正切值等于________.
13.已知球面上A、B两点间的球面距离是1,过这两点的球面半径的
夹角为60°,则这个球的表面积与球的体积之比是
.
14.下面是关于三棱锥的四个命题:
①底面是等边三角形,侧面与底面所成的二面角都相等的三棱锥是正三棱锥. ②底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥. ③底面是等边三角形,侧面的面积都相等的三棱锥是正三棱锥.
④侧棱与底面所成的角都相等,且侧面与底面所成的二面角都相等的三棱锥是正三棱锥. 其中,真命题的编号是______________(写出所有真命题的编号).
15.(2005年全国Ⅰ高考题)在正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,则
① 四边形BFD1E一定是平行四边形 ② 四边形
BFD1E有可能是正方形
③ 四边形BFD1E在底面ABCD内的投影一定是正方形 ④ 四边形BFD1E有可能垂直于平面BB1D
以上结论正确的为 (写出所有正确结论的编号).
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分l2分)
在四棱锥V-ABCD中,底面ABCD是正方形, 侧面VAD是正三角形,平面VAD⊥底面ABCD. (Ⅰ)证明AB⊥平面VAD.
(Ⅱ)求面VAD与面VDB所成的二面角的大小.
17.(本题满分12分)(2005年湖南高考题)
如图1,已知ABCD是上、下底边长分别是2和6,高为3的等腰梯形.将它沿对称轴
OO1折成直二面角,如图2.
O1
B
(Ⅰ)证明AC⊥BO1;
(Ⅱ)求二面角O-AC-O1的大小.
18.(本题满分14分)
如图,在底面是矩形的四棱锥P—ABCD中,PA⊥底面ABCD,PA=AB=1,BC=2. (1)求证:平面PDC⊥平面PAD;
(2)若E是PD的中点,求异面直线AE与PC所成角的余弦值;
(3)在BC边上是否存在一点G,使得D点到平面PAG的距离为1,若存在,求出BG的值;若不存在,请说明理由.
C
E
D
19.(本题满分14分)
如图,已知三棱柱ABC-A1B1C1的底面是边长为2的正三角形,侧棱A1A与AB、AC均成45°角,且A1E⊥B1B于E,A1F⊥CC1于F. C1 A⑴求证:平面A1EF⊥平面B1BCC1; ⑵求直线AA1到平面B1BCC1的距离; ⑶当AA1多长时,点A1到平面ABC与平面B1BCC1的距离相等.
C
B
20.(本题满分14分)
?,OC=2,OA=AB=1,SO⊥平面OABC,2
SO=1,以OC、OA、OS分别为x轴、y轴、z轴建立直角坐标系O-xyz.
????????
⑴求SC与OB的夹角?的大小(用反三角函数表示);
如图直角梯形OABC中,
∠COA=∠OAB=
⑵设?(1,p,q),满足?平面SBC,求:
?
①n的坐标;
②OA与平面SBC的夹角?(用反三角函数表示);
③O到平面SBC的距离.
⑶设k?(1,r,s)满足k?SC且k?OB.填写:
①
②异面直线SC、OB的距离为 .(注:⑶只要求写出答案)
21.(本题满分14分)
直三棱柱ABC-A1B1C1,底面△ABC中,CA=CB=a,∠BCA=90°,AA1=2a,M、N分别是A1B1、AA1的中点. (I)求的长;
(II)求cos〈BA; 1,CB1〉
(III)求证:A1B⊥C1M.
2高三数学2单元测试卷(十)
第十单元 空间向量及运算
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合题目要求的. 1.在平行六面体ABCD—A1B1C1D1中,设AC1?xAB?2yBC?3zCC1,则x+y+z等于 A.1
2B.
3
5C
6
11D.664D.
9
??????????????????
2.设a=(x,4,3),b=(3,2,z),且a∥b,则xz的值为 A.9
B.-9
C.4
????
3.已知A(1,2,-1)关于面xoy的对称点为B,而B关于x轴对称的点为C,则BC?
A.(0,4,2)
B.(0,-4,-2)
C.(0,4,0)
D.(2,0,-2)
?????4.如图,在四面体O—ABC中,是M在OA上,且OM=2MA,N为BC中点,则MN?
?2????1????1???
A.OA?OB?OC
232
?1????1????2???
C.?OA?OB?OC
322
?1????2????1???
B.OA?OB?OC
223
?2????1????2???
D.OA?OB?OC
332
D.-15
5.已知a=3i+2j-k,b=i-j+2k,则5a与3b的数量积等于
A.-1 B.-3 C.-5
????????????
6.设空间四点O,A,B,P,满足OP?OA?tAB, 其中0<t<1,则有
A.点P在线段AB上 B.点P在线段AB的延长线上 C.点P在线段BA的延长线上 D.点P不一定在直线AB上 7.已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相垂直,则k等于 A.1
1
B.
5
3
C
5
7D.
5
????????????????????????
8.设A、B、C、D是空间不共面的四点,且满足AB?AC?0,AC?AD?0,AB?AD?0,则
B、C、D三点构成
A.直角三角形 B.锐角三角形 C.钝角三角形 D.形状不能确定
?????????????
9.若向量MA,MB,MC的起点与终点M、A、B、C互不重合且无三点共线,且满足下列关
?????????????
系(O为空间任一点),则能使向量MA,MB,MC成为空间一组基底的关系是 ?????1????1????1???? A.OM?OA?OB?OC
333?????????1????2????C.OM?OA?OB?OC
33
?????????????
B.MA?MB?MC ?????????????D.MA?2MB?MC
10.已知a=(cosα,1,sinα),b=(sinα,1,cosα),且sinα≠cosα,则向量a+b与a-b的夹角是
A.0° B.30° C.60° D.90°
答题卡
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.已知a=(2,-1,2),b=(2,2,1),则以a,b为邻边的平行四边形的面积为. 12.与向量a=(2,-1,2)共线,且满足方程a2x= -18的向量x=
????
13.若点A、B的坐标为A(3cosα,3sinα,1)、B(2cosθ,2sinθ,1)则 |AB|取值范围 .
????????????????14.已知G是△ABC的重心,O是空间与G不重合的任一点,若OA?OB?OC??OG,
则λ= .
15.已知a=(a1,a2,a3),b=(b1,b2,b3),且|a|=5,|b|=6,a2b=30,则
a1?a2?a3
b1?b2?b3
? .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本题满分l2分)
已知a=(1,1,0),b=(1,1,1),若b=b1+b2,且b1∥a,b2⊥a,试求b1,b2. 17.(本题满分12分)
如图,BC=2,原点O是BC的中点,点A
的坐标为且∠BDC=90°,∠DCB=30°. 1,0),点D在平面yoz上,22
???? ⑴求向量CD的坐标;
⑵求异面直线AD与BC所成角的余弦值.
18.(本题满分14分)
已知a,b是非零的空间向量,t是实数,设u=a+tb.
⑴当|u|取得最小值时,求实数t 的值;
⑵当|u|取得最小值时,求证:b⊥(a+tb).
19.(本题满分14分)
1如图,已知四面体O—ABC中,E、F分别为AB,OC上的点,且AE=AB,F为中点,3
若AB=3,BC=1,BO=2,且∠ABC=90°,∠OBA=∠OBC=60°,求异面直线OE与BF所成角的余弦值.
20.(本题满分14分)
已知正方体ABCD—A1B1C1D1的棱长为2,P,Q分别是BC,CD上的动点,且|PQ|=2,建立如图所示的直角坐标系.
⑴确定P,Q的位置,使得B1Q⊥D1P;
⑵当B1Q⊥D1P时,求二面角C1—PQ—C的正切值.
21.(本题满分14分)
如图,正三棱柱ABC—A1B1C1的各棱长都是2,M是BC的中点,P是侧棱BB1上一点,且A1P⊥B1M.
⑴试求A1P与平面APC所成角的正弦;
⑵求点A1到平面APC的距离.
2高三数学2单元测试卷(十一)
第十一单元 排列组合、二项式定理
(时量:120分钟 150分)
一、选择题:本大题共18小题,每小题5分,共90分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.5人排一个5天的值日表,每天排一人值日,每人可以排多天或不排,但相邻两天不能排同一人,值日表排法的总数为
A.120 B.324 C.720 D.1280
2.一次考试中,要求考生从试卷上的9个题目中选6个进行答题,要求至少包含前5个题目中的3个,则考生答题的不同选法的种数是
A.40 B.74 C.84 D.200
3.以三棱柱的六个顶点中的四个顶点为顶点的三棱锥有
A.18个 B.15个 C.12个 D.9个
4.从一架钢琴挑出的十个音键中,分别选择3个,4个,5个,?,10个键同时按下,可发出和弦,若有一个音键不同,则发出不同的和弦,则这样的不同的和弦种数是
A.512 B.968 C.1013 D.1024
5
.如果(x?n的展开式中所有奇数项的系数和等于512,则展开式的中间项是
68 A.C10x B
.C10x5 46C.C8x D
.C11x66.用0,3,4,5,6排成无重复字的五位数,要求偶数字相邻,奇数字也相邻,则这样的五位数的个数是
A.36 B.32 C.24 D.20
1n?12n?2n?17.若n是奇数,则7n?Cn7?Cn7????Cn7被9除的余数是
A.0 B.2 C.7 D.8
8.现有一个碱基A,2个碱基C,3个碱基G,由这6个碱基组成的不同的碱基序列有
A.20个 B.60个 C.120个 D.90个
9.某班新年联欢会原定的6个节目已排成节目单,开演前又增加了3个新节目,如果将这3个节目插入原节目单中,那么不同的插法种数为
A.504 B.210 C.336 D.120
10.在(1?x)3?(1?x)4????(1?x)2005的展开式中,x3的系数等于
4 A.C2005 4B.C2006 3C.C2005 3D.C2006
11.现有男女学生共8人,从男生中选2人,从女生中选1人,分别参加数理化三科竞赛,共有90种不同方案,则男、女生人数可能是
A.2男6女 B.3男5女 C.5男3女 D.6男2女
512.若x∈R,n∈N+ ,定义Mxn=x(x+1)(x+2)?(x+n-1),例如M?5=(-5)(-4)(-3)(-
2)(-1)=-120,则函数f(x)?xM19
x?9的奇偶性为
A.是偶函数而不是奇函数
C.既是奇函数又是偶函数 B.是奇函数而不是偶函数 D.既不是奇函数又不是偶函数
13.由等式x4?a1x3?a2x2?a3x?a4?(x?1)4?b1(x?1)3?b2(x?1)2?b3(x?1)?b4,定
义映射f:(a1,a2,a3,a4)?(b1,b2,b3,b4),则f(4,3,2,1)等于
A.(1,2,3,4)
B.(0,3,4,0) D.(0,-3,4,-1) C.(-1,0,2,-2)
14.已知集合A={1,2,3},B={4,5,6},从A到B的映射f(x),B中有且仅有2个元
素有原象,则这样的映射个数为
A.8 B.9 C.24 D.27
15.有五名学生站成一排照毕业纪念照,其中甲不排在乙的左边,又不与乙相邻,而不同的
站法有
A.24种 B.36种 C.60种 D.66种
16.等腰三角形的三边均为正数,它们周长不大于10,这样不同形状的三角形的种数为
A.8 B.9 C.10 D.11
17.甲、乙、丙三同学在课余时间负责一个计算机房的周一至周六的值班工作,每天1人值
班,每人值班2天,如果甲同学不值周一的班,乙同学不值周六的班,则可以排出不同的值班表有
A.36种 B.42种 C.50种 D.72种
10210218
.若x)?a0?a1x?a则(a)2?(a) 2x???a10x,0?a2???a101?a3???a9
的值为
A.0 B.2
答题卡
二、填空题:本大题共6小题,每小题4分,共24分.把答案填在横线上.
19.某电子器件的电路中,在A,B之间有C,D,E,F四个焊点(如图),如果焊点脱落,
则可能导致电路不通.今发现A,B间电路不通,则焊点脱落的不同情况有 种.
20.设f(x)=x5-5x4+10x3-10x2+5x+1,则f(x)的反函数f1(x)= -C.-1 D.1
21.正整数a1a2?an?a2n-2a2n-1称为凹数,如果a1>a2>?an,且a2n-1>a2n-2>?>an,其中ai
(i=1,2,3,?)∈{0,1,2,?,9},请回答三位凹数a1a2a3(a1≠a3)共有 个(用数字作答).
22.如果a1(x-1)4+a2(x-1)3+a3(x-1)2+a4(x-1)+a5=x4,那么a2-a3+a4.
23.一栋7层的楼房备有电梯,在一楼有甲、乙、丙三人进了电梯,则满足有且仅有一人要
上7楼,且甲不在2楼下电梯的所有可能情况种数有 .
6224.已知(x+1)(ax-1)的展开式中,x3的系数是56,则实数a的值为 .
三、解答题:本大题共3小题,共36分.解答应写出文字说明,证明过程或演算步骤.
25.(本小题满分12分)
将7个相同的小球任意放入四个不同的盒子中,每个盒子都不空,共有多少种不同的方法?
26.(本小题满分12分)
已知413 +x)n展开式中的倒数第三项的系数为45,求: x
⑴含x3的项;
⑵系数最大的项.
27.(本小题满分12分)
123n求证:1?4Cn?7Cn?10Cn???(3n?1)Cn?(3n?2)?2n?1.
2高三数学2单元测试卷(十二)
第十二单元 [排组]到[概率],算法找规律
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有
一项是符合题目要求的.
1.将4名教师分配到3种中学任教,每所中学至少1名教师,则不同的分配方案共有 A.12种
B.24种
C.36种
D.48种
2.某班新年联欢会原定的5个节目已排成节目单, 开演前又增加了两个新节目.如果将这两个新节目插入原节目单中, 那么不同插法的种数为 A.42
B.96
C.124
D.48
B.20种
C.18种
D.12种
3.将1-9这9个不同的数字分别填入右图中的方格中,要求每行自左至右数字从小到大排,每列自上到下数字也从小到大排,并且5排在正中的方格,则不同的填法共有 A.24种
4.从4名男生和3名女生中选出4人参加某个座谈会,若这4人中必须既有男生又有女生,则不同的选法共有
A.140种 B.120种
C.35种
D.34种
5.某人射击一次击中的概率为0.6,经过3次射击,此人至少有两次击中目标的概率为
81543627A. B.C. D.
1251251251256.(2005年全国Ⅲ高考题) 在(x-1)(x+1)8的展开式中x5的系数是 A.-14
B.14
C.-28
D.28
7.在一次足球预选赛中, 某小组共有5个球队进行双循环赛(每两队之间赛两场), 已知胜一场得3分, 平一场得1分, 负一场的0分. 积分多的前两名可出线(积分相等则要要比净胜球数或进球总数). 赛完后一个队的积分可出现的不同情况种数为 A.22 B.23 C.24
D.25
8.(2005年湖南高考题) 4位同学参加某种形式的竞赛,竞赛规则规定:每位同学必须从甲、乙两道题中任选一题作答,选甲题答对得100分,答错得-100分;选乙题答对得90分,答错得-90分。若4位同学的总分为0,则这4位同学不同得分情况的种数是 A.48
B.36
C.24 D.18
9.四面体的顶点和各棱中点共10个点, 在其中取4个不共面的点, 则不同的取法共有 A.150种
B.147种
C.144种 D.141种
10.从数字1,2,3,4,5中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为 1918A. B.
125125
16
C.
125
13D.125
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
334
11.若Cn?Cn?1?Cn?1,则n的值为.
12.一台X型号自动机床在一小时内不需要工人照看的概率为0.8000,有四台这中型号的自动机床各自独立工作,则在一小时内至多2台机床需要工人照看的概率是 . 13.将标号为1,2,?,10的10个球放入标号为1,2,?,10的10个盒子内, 每个盒
子内放一个球,则恰好有3个球的标号与其所在盒子的标号不一致的放入方法共有 .(以数字作答)
14.若在二项式(x+1)10的展开式中任取一项,则该项的系数为奇数的概率是 .
(结果用分数表示).
15.(2005年湖南高考题)在(1+x)+(1+x)2+?+(1+x)6展开式中,x2的系数是 . (用数字作答)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分l2分)
从1到100的自然数中, 每次取出不同的两个数, 使它的和大于100, 则不同的取法有多少种。 17.(本题满分12分)(2005年全国Ⅰ高考题)
设甲、乙、丙三台机器是否需要照顾相互之间没有影响。已知在某一小时内,甲、乙都需要照顾的概率为0.05,甲、丙都需要照顾的概率为0.1,乙、丙都需要照顾的概率为0.125,
⑴求甲、乙、丙每台机器在这个小时内需要照顾的概率分别是多少; ⑵计算这个小时内至少有一台需要照顾的概率.
18.(本题满分14分)
9粒种子分种在甲、乙、丙3个坑内,每坑3粒,每粒种子发芽的概率为0.5,若一个
坑内至少有1粒种子发芽,则这个坑不需要补种;若一个坑内的种子都没发芽,则这个坑需要补种。
⑴求甲坑不需要补种的概率;
⑵求3个坑中恰有1个坑不需要补种的概率; ⑶求有坑需要补种的概率.
19.(本题满分14分)
甲与乙两人掷硬币,甲用一枚硬币掷3次,记下国徽面朝上的次数为m;乙用一枚硬币掷2次,记下国徽面朝上的次数为n。 ⑴计算国徽面朝上不同次数的概率并填入下表:
⑵现规定:若m>n,则甲胜;若n≥m,则乙胜。你认为这种规定合理吗?为什么?
20.(本题满分14分)
m0
规定Ax其中x?R,m为正整数,且Ax?x(x?1)?(x?m?1),?1,这是排列数
mAn(n,m是正整数,且m?n)的一种推广. 3⑴求A?15的值;
mm?1mmm?1⑵排列数的两个性质:①An?An?nAnn?mAn?1.(其中m,n是正整数)是?1, ②Am否都能推广到Ax(x?R,m是正整数)的情形?若能推广,写出推广的形式并给予证明;
若不能,则说明理由;
3⑶确定函数Ax的单调区间.
21.(本题满分14分)
一个同心圆形花坛,分为两部分,中间小圆部分种植草坪和绿色灌木,周围的圆环分为
n(n?3,n?N)等份,种植红、黄、蓝三色不同的花,要求相邻两部分种植不同颜色的
花.
⑴如图1,圆环分成的3等份为a1,a2,a3,有多少不同的种植方法?如图2,圆环分成
的4等份为a1,a2,a3,a4,有多少不同的种植方法?
⑵如图3,圆环分成的n等份为a1,a2,a3,??,an,有多少不同的种植方法?
2高三数学2单元测试卷(十三)
第十三单元 [统计]到整体,推断与估计
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.10个小球分别编有号码1、2、3、4,其中1号球4个,2号球2个,3号球3个,4号球1个,则数0.4是指1号球占总体分布的 A.频数 B.概率 C.频率 D.累积频率 2.已知10个数据:
1203 1201 1194 1200 1204 1201 1199 1204 1195 1199 它们的平均数是
A.1400 B.1300 C.1200 D.1100
3.某工厂生产A、B、C三种不同型号的产品,产品数量之比依次为2:3:5,现用分层抽样方法抽出一个容量为n的样本,样本中A种型号产品有16件.那么此样本的容量n= A.60
B.70
C.80
D.90
4.若m个数的平均数是x,n个数的平均数是y,则这m+n个数的平均数是
x+yx+ymx+nymx+nyA. B. C. D.2m+nm+nx+y5.为了了解全校1320名高一学生的身高情况,从中抽取220名学生进行测量,下列说法正确的是
A.样本容量是220 B.个体是每一个学生 C.样本是220名学生 D.总体是1320
6.某公司在甲、乙、丙、丁四个地区分别有150个、120个、180个、150个销售点.公司为了调查产品销售的情况,需从这600个销售点中抽取一个容量为100的样本,记这项调查为①;在丙地区中有20个特大型销焦点,要从中抽取7个调查其销售收入和售后服务情况,记这项调查为②.则完成①、②这两项调查宜采用的抽样方法依次是 A.分层抽样,系统抽样法 B.分层抽样法,简单随机抽样法 C.系统抽样法,分层抽样法 D.简随机抽样法,分层抽样法 7.如图所示是一批产品中抽样得到数据的频率直方图, 由图可看出概率最大时数据所在范围是
A.(8.1,8.3) B.(8.2,8.4) C.(8.4,8.5) D.(8.5,8.7)
下面结论正确的是
A.平均数与方差都不变 C.平均数不变,方差变了
8.对一组数据xi(i=1,2,?,n),如将它们改为xi-m(i=1,2,?,n),其中m≠0.则
B.平均数与方差都变了 D.平均数变了,方差不变
9.从5名男生、1名女生中,随机抽取3人,检查他们的英语口语水平,在整个抽样过程
中,若这名女生第一次、第二次均未被抽到,那么她第三次被抽到的概率是
1112A. B C. D.
2633
10.某初级中学有学生270人,其中一年级108人,二、三年级各81人,现要利用抽样方
法抽取10人参加某项调查,考虑选用简单随机抽样、分层抽样和系统抽样三种方案,使用简单随机抽样和分层抽样时,将学生按一、二、三年级依次统一编号为1,2,?,270;使用系统抽样时,将学生统一随机编号为1,2,?,270,并将整个编号依次分为10段.如果抽得号码有下列四种情况: ①7,34,61,88,115,142,169,196,223,250; ②5,9,100,107,111,121,180,195,200,265; ③11,38,65,92,119,146,173,200,227,254; ④30,57,84,111,138,165,192,219,246,270; 关于上述样本的下列结论中,正确的是 A.②、③都不能为系统抽样 B.②、④都不能为分层抽样 C.①、④都可能为系统抽样 D.①、③都可能为分层抽样
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.一个容量为n的样本分成若干组,已知某组的频数和频率分别是20和0.25,则n=. 12
13.若x1,x2,?,x8的方差为3,则2(x1?3),2(x2?3),?2(x8?3)的方差是_____. 14.一个公司有N个员工,下设一些部门,现采用分层抽样方法从全体员工中抽取一个容量为n(N是n的倍数),已知某部门被抽取了m个员工.那么这一部门的员工是 . 15.为科学地比较考试布成绩,有些选拔性考试常常会将考试分数转化为标准分,转化关系
x--x
式为Z=其中x是某位学生的考试分数,-x是该次考试的平均分,s是该次考试
s
的标准差,Z称为这个学生的标准分).转化后可能出现小数和负值,因此又常将Z分数作线性变换为其他分数.如某次学业选拔考试采用的是T分数,线性变换公式是T=40Z+60.已知在这次考试中某位考生的考试分数是85,这次考试的平均分是70,标准差是25.则该考生的T分数是 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
进行随机抽样时,甲学生认为:“每次抽取一个个体时,任一个个体a被抽到的概率”与“在整个抽样过程中个体a被抽到的概率”是一回事,而学生乙则认为两者不是一回事.你认为甲、乙两学生中哪个对?请列举具体例子加以说明.
17.(本小题满分12分)
某人从湖中打了一网鱼,共m条,做上记号再放入湖中,数日后,又从该湖中打了一网鱼共n条,其中k条有记号,估计湖中有多少条鱼?
18.(本小题满分14分)
某农科所为寻找高产稳定的油菜品种,选了三个不同的油菜品种进行试验,每一品种在
五块试验田试种.每块试验田的面积为0.7公顷,产量情况如下表.
试评定哪一品种既高产又稳定.
19.(本小题满分14分)
某医院门诊部关于病人等待挂号的时间记录如下:
试用上述分组资料求出病人平均等待时间的估计值-x及平均等待时间标准差的估计值s. 20.(本小题满分14分)
某电信部门执行的新的电话收费标准中,其中本地网营业区内的通话费标准:前3分钟为0.20元(不足3分钟按3分钟计算),以后的每分钟收0.10元(不足1分钟按1分钟计算。)在一次实习作业中,某同学调查了A、B、C、D、E五人某天拨打的本地网营
⑵设通话时间为t分钟,试根据上表完成下表的填写(即这五人在这一天内的通话情况
⑶若该本地网营业区原来执行的电话收费标准是:每3分钟为0.20元(不足3分钟按3分钟计算)。问这五人这天的实际平均通话费与原通话标准下算出的平均通话费相比,是增多了还是减少了?增或减了多少? 21.(本小题满分14分)
考察某校高三年级男生的身高,随机抽取40名高三男生,实测身高数据(单位:㎝) 如下:
171 163 163 169 166 168 168 160 168 165 171 169 167 159 151 168 170 160 168 174 165 168 174 161 167 156 157 164 169 180 176 157 162 166 158 164 163 163 167 161 ⑴作出频率分布表; ⑵画出频率分布直方图; ⑶估计身高不大于160㎝的概率.
2高三数学2单元测试卷(十四)
第十四单元 导数及应用
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.曲线y=x2+3x在点A(2,10)处的切线的斜率k是 A.4 B.5 C.6 D.7 2.已知二次函数y=ax2+(a2+1)x在x=1处的导数值为1,则该函数的最大值是 25
A.
16
25B.
8
25C
4
25D.
2
x2-1
3.函数y=
xx2-1
A.
x
x2+1B.
x
x2-1C
x
1-x2D.
x
4.已知函数f(x-1)=2x2-x,则f′(x)= A.4x+3 B.4x-1 C.4x-5 D.4x-3 5.曲线y=x3的切线中斜率等于1的直线 A.不存在 B.存在,有且仅有一条 C.存在,有且恰有两条 D.存在,但条数不确定 6.已知函数f(x)=(x-1)(x-2)(x-3)??(x-100),则f′(1)=
A.-99! B.-100! C.-98! D.0
7.已知f(x)=2x3-6x2+a(a是常数)在[-2,2]上有最大值3,那么在[-2,2]上的最小值是 A.-5 B.-11 C.-29 D.-37 18.设过曲线xy=1上两点P1(1,1),P2(2,)的切线分别是l1、l2,那么l1与l2夹角的正切值为
23A.-
5
3B.
4
4C
5
3D.
5
9.已知一个物体的运动方程是s=1-t+t2,其中s的单位是米,t的单位是秒,那么该物体
在3秒末的瞬间速度是 A.6米/秒 B.7米/秒 C.8米/秒 D.9米/秒
32
10.已知函数f(x)=x-ax+1在区间(0,2)内单调递减,则实数a的取值范围是 A.a≥3 B.a=3 C.a≤3 D.0<a<3
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上. 11.过点(0,-4)与曲线y=x3+x-2相切的直线方程是 . 12.设y=3
2x
y′= .
12
13.以函数y?x为导数的函数f(x)图象过点(9,1),则函数f(x)= 14.已知函数f(x)是定义在区间(-1,1)上的奇函数,且对于x∈(-1,1)恒有f’(x)<0成立,若f(-2a2+2)+f(a2+2a+1)<0,则实数a的取值范围是 . 15.已知函数f(x)是定义在实数集R上的函数,给出下列结论: ①若存在常数x0,使f’(x)=0,则函数f(x)必在x0处取得极值;
②若函数f(x)在x0处取得极值,则函数f(x)在x0处必可导;
③若函数f(x)在R上处处可导,则它有极小值就是它在R上的最小值; ④若对于任意x≠x0都有f’(x)>f(x),则f(x0)是函数f(x)的最小值;
⑤若对于任意x<x0有f’(x)>0,对于任意x>x0有f’(x)<0,则f(x0)是函数f(x)的一个最大值;
其中正确结论的序号是 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
?x2?ax(x?1)
设函数f(x)??求实数a、b的值和该函数,若该函数在实数集R上可导,
?x?b(x?1)
的最小值.
17.(本小题满分12分)
1
已知曲线C1:y=x2-2x+2和曲线C2:y=x3-3x2+5有一个公共点P(2,2),若
2α+βα+β
两曲线在点P处的切线的倾斜角分别是α和β,求tansin
23
18.(本小题满分14分)
已知函数f(x)=ax3-6ax2+b(x∈[-1,2])的最大值为3,最小值为-29,求a、b的值.
19.(本小题满分14分)
将边长为a的一块正方形铁皮的四角各截去一个大小相同的小正方形,然后将四边折起做成一个无盖的方盒.欲使所得的方盒有最大容积,截去的小正方形的边长应为多少?方盒的最大容积为多少? 20.(本小题满分14分).
已知函数f(x)=x4-4x3+ax2-1在区间[0,1]上单调递增,在区间[1,2]上单调递减;
⑴求a的值;
⑵是否存在实数b,使得函数g(x)=bx2-1的图象与函数f(x)的图象恰有2个交点,若存在,求出实数b的值;若不存在,试说明理由.
21.(本小题满分14分)
已知二次函数y=g(x)的图象经过原点O(0,0)、点P1(m,0)和点P2(m+1,m+1)(m≠0,且m≠1).
⑴求函数y=g(x)的解析式;
⑵设f(x)=(x-n)g(x)(m>n>0)在x=a和x=b(b<a)处取得极值. (ⅰ)求证b<n<a<m;
(ⅱ)若m+n=22,则过原点与曲线y=f(x)相切的两条直线能否互相垂直?若能,请给出证明;若不能,请说明理由.
2高三数学2单元测试卷(十五)
第十五单元 函数与方程思想
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.设直线 ax+by+c=0的倾斜角为?,且sin?+cos?=0,则a,b满足
A.a?b?1
B.a?b?1
C.a?b?0
D.a?b?0
2.设P是60°的二面角α-l-β内一点,PA⊥平面α,PB⊥平面β,A、B为垂足,PA=4,
PB=2,则AB的长为 A.3
B.25
C.27
D.2
3. 若{an}是等差数列,首项a1?0,a2003?a2004?0,a2003.a2004?0,则使前n项和Sn?0
成立的最大自然数n是 A.4005
B.4006
C.4007
D.4008
4.每个顶点的棱数均为三条的正多面体共有 A.2种 5.设函数f(x)??
B.3种
C.4种 D.5种
x
(x?R),区间M=[a,b](a<b),集合N={yy?f(x),x?M},则1?x
使M=N成立的实数对(a,b)有
A.0个
?1
B.1个 C.2个 D.无数多个
6.设f
为
(x)是函数f(x)?log2(x?1)的反函数,若[1?f?1(a)][1?f?1(b)]?8,则f(a?b)的值
A.1 B.2 C.3
D.log23
7.把正方形ABCD沿对角线AC折起,当A、B C、D四点为顶点的三棱锥体积最大时,
直线BD与平面ABC所成的角的大小为
A.90°
B.60°
C.45°
D.30°
8.若函数f(x)=(1-m)x2-2mx-5是偶函数,则f(x)
A.先增后减
B.先减后增
C.单调递增
D.单调递减
9.定义在(-∞,+∞)上的奇函数f(x)和偶函数g(x)在区间(-∞,0]上的图像关于x轴对称,且f(x)为增函数,则下列各选项中能使不等式f(b)-f(-a)>g(a)-g(-b)成立的是
A.a>b>0
B.a<b<0
C.ab>0
D.ab<0
10.△ABC中,a、b、c分别为∠A、∠B、∠C的对边.如果a、b、c成等差数列∠B=30°,
3
△ABC的面积为,那么b=
2
1+3A.2
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
B.1+3 2+C.2
D.2+3
x2y2
??1的离心11.两个正数a、b的等差中项是5,等比中项是4.若a>b,则双曲线ab
率e等于 . 12.若(x?
1
?2)n的展开式中常数项为-20,则自然数n= x
13.x0是x的方程ax=logax(0<a<1)的解,则x0,1,a这三个数的大小关系是 .
14.已知函数y?f(x)与y?f
?1
(x)互为反函数,又y?f
?1
(x?1)与y?g(x)的图象关
?1
于直线y?x对称,若f(x)?log1(x2?2)(x?0),则f
2
(x)?_;
g()?.
15.已知矩形ABCD的边AB?a,BC?2,PA?平面ABCD,PA?2,现有以下五个数据:
1
(1)a?;(2)a?1;(3)a?;(4)a?2;(5)a?4,当在BC边上存在点Q,
2
使PQ?QD时,则a可以取_____________.(填上一个正确的数据序号即可)
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本小题满分12分)
已知集合A={x|x2-ax+a2-19=0},集合B={x|log2(x2-5x+8)=1},集合C={x|m
x2?2x?8
=1,m≠0,|m|≠1}满足A∩B
?, A∩C=?,求实数a的值.
17.(本小题满分12分)
有一组数据:x1,x2,?,xn(x1?x2???xn)的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据 的算术平均值为11.
(1)求出第一个数x1关于n的表达式及第n个数xn关于n的表达式;
(2)若x1,x2,?,xn都是正整数,试求第n个数xn的最大值,并举出满足题目要求且xn取到最大值的一组数据.
18.(本小题满分14分) 求函数f(x)?ln(1?x)?
19.(本小题满分14分)
某公司生产的A型商品通过租赁柜台进入某商场销售.第一年,商场为吸引厂家,决定免收该年管理费,因此,该年A型商品定价为每件70元,年销售量为11.8万件.第二年,商场开始对该商品征收比率为p%的管理费(即销售100元要征收p元),于是该商品的定价上升为每件
12
x在[0,2]上的最大值和最小值. 4
70
元,预计年销售量将减少p万件.
1?p%
(1)将第二年商场对该商品征收的管理费y(万元)表示成p的函数,并指出这个函数的定义域;
(2)要使第二年商场在此项经营中收取的管理费不少于14万元,则商场对该商品征收
管理费的比率p%的范围是多少?
(3)第二年,商场在所收管理费不少于14万元的前提下,要让厂家获得最大销售金额,则p应为多少?
20.(本小题满分14分)
已知二次函数f(x)=ax2+bx(a,b为常数,且a≠0)满足条件: f(x-1)=f(3-x)且方程f(x)=2x有等根. (1)求f(x)的解析式;
(2)是否存在实数m,n(m<n),使f(x)的定义域和值域分别为[m,n]和[4m,4n],如果存在,求出m,n的值;如果不存在,说明理由. 21.(本小题满分14分)
设无穷等差数列{an}的前n项和为Sn.
3
(1)若首项a1? ,公差d?1,求满足S2?(Sk)2的正整数k;
2k (2)求所有的无穷等差数列{an},使得对于一切正整数k都有S
k2
?(Sk)2成立.
2高三数学2单元测试卷(十六) 第十六单元 数形结合思想
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.设全集U=R,集合A=(1,+∞),集合B=(-∞,2)。则eU(A∩B)= A.(-∞,1)∪(2,+∞) B.(-∞,1)∪[2,+∞) C.(-∞,1]∪[2,+∞) D.(-∞,1]∪(2,+∞)
2.如图,直线Ax+By+C=0(AB≠0)的右下方有一点(m,n),则Am+Bn+C的值 A.与A同号,与B同号 B.与A同号,与B异号 C.与A异号,与B同号 D.与A异号,与B异号
3.设方程2x+x+2=0和方程log2x+x+2=0的根分别为p和q,函数f(x)=(x+p)(x+q)+2,则
A.f(2)=f(0)<f(3) B.f(0)<f(2)<f(3) C.f(3)<f(0)=f(2) D.f(0)<f(3)<f(2)
??x-2≤0,
4.已知点P(x,y)在不等式?y-1≤0,表示的平面区域上运动,则z=x-y的取值范围是
?x+2y-2≥0?
A.[-2,-1] B.[-2,1] C.[-1,2] D.[1,2]
5.若定义在区间(―1,0)内的函数f(x)?log2(x?1)满足f(x)?0,则a的取值范围是 A.(0,)
12
B.(0,]
12
C.(,??)
12
D.(0,??)
6.如图,B地在A地的正东方向4 km处,C地在B地
的北偏东30°方向2 km处,河流的没岸PQ(曲线)上任意一点到A的距离比到B的距离远2 km.现要在曲线PQ上选一处M建一座码头,向B、C两地转运货物.经测算,从M到B、M到C修建公路的费用分别是a万元/km、2a万元/km,那么修建这两条公路的总费用最低是
A.7-2)a万元 B.5a万元
C.7+1) a万元 D.(23+3) a万元 7.如图,在正方体ABCD-A1B1C1D1中,点E在A1D上且A1E=2ED,A点F在AC上且CF=2FA,则EF与BD1的位置关系是 A.相交不垂直 B.相交垂直 C.平行 D.异面
8.在(0,2π)内,使sinx>cosx成立的x取值范围为
ππ5ππ
A.)∪(π, B.π)
4244π5π
C.)
44
π5π3π
D.(π)∪()
442
1
1
C 9.椭圆上一点A看两焦点的视角为直角,设AF1的延长线交椭圆于B,又|AB|=|AF2|,则
椭圆的离心率e= A.-2+2 B.6-3 C2-1 D.3-2
22
10.过原点的直线与圆x+y+4x+3=0相切,若切点在第三象限,则该直线的方程是 A.y3x
B.y=-3x 答题卡
C.y=
33
D.y=-
33x
11.设奇函数f(x)的定义域为[-5,5].若当x∈[0,5]时,
f(x)的图象如右图,则不等式f(x)<0的解是12.设x,y满足约束条件:
?x?0,?
?x?y,
?2x?y?1,?
则z=3x+2y的最大值是 13.据新华社2002年3月12日电,1985年到2000 年间,我国农村人均居住面积如图所示,其中, 从年的五年间增长最快。 14.有两个相同的直三棱柱,高为
2
,底面三角形的三边长分a
别为3a、4a、5a(a>0).用它们拼成一个三棱柱或四棱柱,在所有可能的情况中,全面积最小的是一个四棱柱,则a的取值范围是 . 15.给出下列图象
其中可能为函数f(x)=x4+ax3+bx2+cx+d(a,b,c,d∈R)的图象的是_____.
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分12分) 已知函数f(x)
?sin(
?7??
?x)?cos(x
?)的图象向右平移
个单位得到函数g(x)的图象.
888
⑴求函数
g(x)的表达式; ⑵证明当x?(
3?5?
)时,经过函数g(x)图象上任意两点的直线的斜率恒大于零. 44
17.(本小题满分12分)
如图所示,已知四面体O?ABC中,M为BC的中点,N为AC的中点,Q为OB的中点,
P为OA的中点,若AB?OC,试用向量方法证明:PM?QN.
A C
B 18.(本小题满分14分)为了能更好地了解鲸的生活习性,某动物研究所在受伤的鲸身上安
装了电子监测装置,从海岸放归点A处(如图所示)把它放归大海,并沿海岸线由西到东不停地对鲸进行了40分钟的跟踪观测,每隔10分钟踩点测得数据如下表(设鲸沿海面游动)。然后又在观测站B处对鲸进行生活习性的详细观测。已知AB=15km,观测站B的观测半径为5km
.
(I)根据表中数据:(1)计算鲸沿海岸线方向运动的速度,(2)写出a、b满足的关系式,并画出鲸的运动路线简图;
(II)若鲸继续以(I)-(2)中的运行路线运动,则鲸经过多少分钟(从放归时计时),可进入前方观测站B的观测范围。41≈6.4)
19.(本小题满分14分)如图所示,已知圆C:(x?1)2?y2?8,定点A(1,0),M为圆上
??????????????????
一动点,点P在AM上,点N在CM上,且满足AM?2AP,NP?AM?0,点N的轨迹
为 曲线E.
(I)求曲线E的方程;
(II)若过定点F(0,2)的直线交曲线E于不同的两点G、H(点G在点F、H之间),
????????
且满足FG??FH,求?的取值范围.
20.(本小题满分14分)已知二次函数y=f1(x)的图象以原点为顶点且过点(1,1),反比例函数y=f2(x)的图象与直线y=x的两个交点间距离为8,f(x)= f1(x)+ f2(x). (1) 求函数f(x)的表达式;
(2) 证明:当a>3时,关于x的方程f(x)= f(a)有三个不同的实数解.
21.(本小题满分14分) 已知a?1,数列{an}的通项公式是an?
1a
n?2
,前n项和记作
2,?),规定S0?0.函数f(x)在S0处和每个区间(Si,Si?1)(i?0,1,2,?)Sn(n?1,
上有定义,且f(S0)?0,f(Si)?ai(i?1,2,?).当x?(Si,Si?1)时,f(x)的图像完全落在连结点Pi(Si,f(Si))与点Pi?1(Si?1,f(Si?1))的线段上. (Ⅰ)求f(x)的定义域;
(Ⅱ)设f(x)的图像与坐标轴及直线l:x?Sn(n?1,2,?)围成的图形面积为An, 求An及
limAn;
n??
(Ⅲ)若存在正整数n,使得An?a2,求a的取值范围.
2高三数学2单元测试卷(十七)
第十七单元 分类与整合思想
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知函数f(x)=loga x在[2,π]上的最大值比最小值大1,则a等于
2π2πA. B C.或 D.不同于A、B、C答案
π2π2
x2y2??1的离心率 e=-2.已知椭圆, 则m的值为 5m5
A.3
25
B3
3
C. D.
5或 3
3.设P=loga(a2+1), Q=loga(a3+1),a>0且a≠1,则P、Q的大小关系是 A.P>Q B.P<Q
C.P=Q
D.与a 有关
4.已知二次函数f(x)=ax2+2ax+1在区间[-3,2]上的最大值为4,则a的值为
33
A.-3 B.- C.3 D.-3或
882
5.如果loga<1,那么a的取值范围是
32
A.(0,)∪(1,+∞)
32
C.,1)
3
2
B.(, +∞)
322
D.(0)∪(,+∞)
33
6.函数y=logax在x∈[2,+∞)上恒有|y|>1,则a的取值范围为
11A.a<2,且a≠1 B.0<a<1<a<2
22C. 1<a<2
1
D. a>2或0<a<2
7.若对任意x∈R,(m-2)x2+4(2―m)x―4的值恒为负值,则m的取值范围为 A.(1, 2)
B.(-∞,2) C.(1,2] D.(∞,2]
8.设0< x <1,0<a≠1,则 A.|loga(1-x)|<| loga(1+x)|
B.|loga(1-x)|=| loga(1+x)|
D.|loga(1-x)|与| loga(1+x)|的大小与a值有关
C.|loga(1-x)|>| loga(1+x)|
9.已知线段AB在平面α外,A、B两点到平面α的距离分别为1和3,则线段AB的中点到平面α的距离为 A.1
B.2
C.1或2
D.0或1
10.若函数f(x)?1111(a?1)x3?ax2?x?在其定义域内有极值点,则a的取值为 3245
B.a=1 A.?2??2? ?a?22
C.?2??2?或a=1 ?a?22D
.?2?2?或a=1
?a?22
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
11.设一双曲线的两条渐近线方程为2x-y+1=0, 2x+y-5=0,此双曲线的离心率为
12.在一块并排10垄的田地中,选择2垄分别种植A、B两种作物,每种作物种植一垄,
为有利于作物生长,要求A、B两种作物的间隔不小于6垄,则不同的选垄方法共
有 种.
13.已知0?x???sinx,则tanx= 2
2??x?x?2?0 ①14.若不等式组?2的解集中的整数有且只有—2,则a的取值范 ②??2x?(5?2a)x?5a?0
围 .
15.从1,3,5,7中任取2个数字,从0,2,4,6,8中任取2个数字,组成没有重复数
字的四位数,其中能被5整除的四位数共有 个(用数字作答).
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤.
16.(本题满分12分)
已知函数f(x)=cos2x+asinx-a2+2a+5.有最大值2,求实数a的值.
17.(本小题满分12分)
解关于x的不等式ax2-2≥2x-ax(a∈R).
18.(本小题满分14分)
设a为实数,函数f(x)?x?|x?a|?1,x?R
(1)讨论f(x)的奇偶性;
(2)求f(x)的最小值.
2
19.(本小题满分14分)
已知方程kx+y=4,其中k为实数,对于不同范围的k值,分别指出方程所代表图形的类型,并画出曲线简图.
20.(本小题满分14分)
已知函数f(x)?ax2?bx(a?0)满足f(2) = 0且方程f(x) = x有两个相等的实根。
(1)求f(x)的解析式:
(2)是否存在m、n∈R(m < n),使f(x)的定义域为[m, n]且值域为[2m, 2n]?若存在,找出所有m , n;若不存在,请说明理由。
22
21.(本小题满分14分)
已知数列{an}、{bn}满足:a1?1,a2?a(a为常数),且bn?an?an?1,其中n?1,2,3?
(Ⅰ)若{an}是等比数列,试求数列{bn}的前n项和Sn的公式; (Ⅱ)当{bn}是等比数列时,甲同学说:{an}一定是等比数列;乙同学说:{an}一定不是等比数列,你认为他们的说法是否正确?为什么?
2高三数学2单元测试卷(十八)
第十八单元 化归与转化思想
(时量:120分钟 150分)
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中, 只有一项是符合题目要求的.
1.一个四面体所有棱长都是2,四个顶点在同一球面上,则此球表面积为
A.3π B.4π C.3π D.6π 2.已知函数y?f(x)与函数y?g(x)图象如下图
则函数y?f(x)?g(x)图象可能是
1
3.设函数f(x)(x∈R)为奇函数,f(1)=,f(x+2)=f(x)+f(2),则f(5)=
2
5
A.0 B.1 C. D.5
2
π
4.已知球O的半径为1,A、B、C三点都在球面上,且每两点间的球面距离均为,则球
2
心O到平面ABC的距离为
1326A B C. D.
33335.已知两条直线l1:y=x,l2:ax–y=0,其中a∈R,当这两条直线的夹角在(0,时,a的取值范围是
3
1)∪(1,3) D.(1,3) 3
aS4n
6.等差数列{an}和{bn}的前n项和分别用Sn和Tn表示,若=,则limn的值为
Tn3n+5n??bA.(0,1)
B.
C.(
n
?
)内变动2
3
3) 3
A.
464 B.1 C D393
4
C12
B.1?4
12
4C12C.4
12
7.某房间有4个人,那么至少有2人生日是同一个月的概率是
4A12
A.4
12
4A
12
D.1
?
4
12
8.(2005年湖北高考题)在y?2x,y?log2x,y?x2,y?cos2x这四个函数中,当
0?x1?x2?1时,使f(
x1?x2f(x1)?f(x2)
?恒成立的函数的个数是 22
A.0 B.1 C.2 D.3
9.(2005年辽宁高考题)在R上定义运算?:x?y?x(1?y).若不等式(x?a)?(x?a)?1
对任意实数x成立,则
1331
A.-1<a<1 B.0<a<2 Ca< D.-a<
2222
10.(2005年上海高考题)用n个不同的实数a1,a2,?,an可得n!个不同的排列,每个排列
为一行写成一个n!行的数阵.对第i行ai1,ai2,?,ain,记bi=-ai1+2ai21 2 3 -3ai3+?+(-1)nnain,i=1,2,3,?,n!.用1,2,3可得数阵如右,由1 3 2 于此数阵中每一列各数之和都是12,所以,b1+b2+┄+b6=-12+2?12
2 1 3
-3?12=-24.那么,在用1,2,3,4,5形成的数阵中,b1+b2+┄+b120
2 3 1 等于 3 1 2 A.-3600 B.1800 C.-1080 D.-720
3 2 1
二、填空题:本大题共5小题,每小题4分,共20分.把答案填在横线上.
11.在等差数列{an}中,若a10=0,则有等式a1+a2+?+an=a1+a2+?+a19-n(n<19,n
*
∈N)成立,类比上述性质,在等比数列{bn}中,b9=1,则有 等式 成立.
12.如图,正三棱锥P-ABC中,各条棱的长都是2,E是侧棱PC的中点,D是侧棱PB
上任一点,则△ADE的最
小周长为 。
E 13.已知a,b为不垂直
的异面直线,α是一
个平面,则a、b在
D α上的射影有可能是 C A C
①两条平行直线; ②两条互相垂直的直线; ③同一条直线; B B ④一条直线及其外一点. 在上面的结论中,正确结
论的编号是 (写出所有正确结论的序号编号).
14.一条路上共有9个路灯,为了节约用电,拟关闭其中3个,要求两端的路灯不能关闭,任意两个相邻的路灯不能同时关闭,那么关闭路灯的方法总数为 . 15.m,n是平面?.,?外两条直线,给出四个论断:
①m?n ②m?? ③n?? ④???
以其中三个论断为条件,余下论断为结论,写出所有正确的命题 .
三、解答题:本大题共6小题,共80分.解答应写出文字说明,证明过程或演算步骤. 16.(本题满分12分)
已知x∈R,a为常数,且f(x?a)?出周期,若不是,说明理由.
1?f(x)
,问f(x)是不是周期函数?若是,求
1?f(x)
17.(本小题满分12分)
已知数列?an? (n?N)是首项为a1,公比为q的等比数列.
?
0120123
⑴求和:a1C2; ?a2C2?a3C2,a1C3?a2C3?a2C3?a4C3
⑵由⑴的结果归纳出关于正整数n的一个结论,并加以证明. 18.(本小题满分14分)
已知关于x的方程:x?ax?2ax?a?1?0有且仅有一个实根,求实数a的取值
范围.
3
2
2
19.(本小题满分14分)已知:a1?a2???an?1,ai?0 (i?1,2?n)
222
anana12a21?1
求证:??????
a1?a2a2?a3an?1?anan?a12
20.(本小题满分14分)
已知?,??(0,),且sin?csc??cos(???),a???.当tan?取最大
22
值时,求tan(???)值.
??
21.(本小题满分14分)
某商店进货每件50元,据市场调查,销售价格(每件x元)在50≤x≤80时,每天售出
105
的件数P=。若想每天获得的利润最多,销售价格每件应定为多少元? (x-40)
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网
 爱华网
爱华网