一. 教学内容:
基本初等函数
指数的概念与运算,指数函数,对数的概念与运算,对数函数,幂函数的概念和性质,基本初等函数的应用。
二. 教学重点
幂函数、指数函数、对数函数的图像和性质及其应用
三. 高考要求
1. 指数函数
(1)通过具体实例(如细胞的分裂,药物在人体内残留量的变化等),了解指数函数模型的实际背景;
(2)理解有理指数幂的含义,通过具体实例了解有理指数幂的意义,掌握幂的运算。
(3)理解指数函数的概念和意义,能借助计算器或计算机画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点;
(4)在解决简单实际问题的过程中,体会指数函数是一类重要的函数模型。
2. 对数函数
(1)理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;通过阅读材料,了解对数的发现历史以及对简化运算的作用;
(2)通过具体实例,直观了解对数函数模型所刻画的数量关系,初步理解对数函数的概念,体会对数函数是一类重要的函数模型;能借助计算器或计算机画出具体对数函数的图象,探索并了解对数函数的单调性与特殊点;
3. 知道指数函数与对数函数互为反函数(a>0,a≠1)。
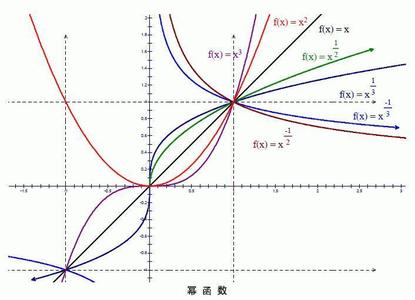
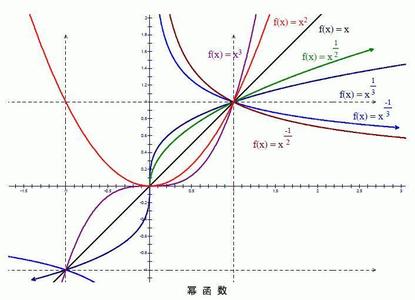
4. (通过实例)了解幂函数的概念;结合函数 的图象,了解它们的变化情况。
5. (利用计算工具,比较)了解指数函数、对数函数以及幂函数增长的差异;(结合实例)体会直线上升、指数增长、对数增长等不同函数类型增长的含义。
【教学过程】
一、基本知识回顾及应用举例
1. 指数与对数运算
(1)根式的概念:
①定义:若一个数的次方等于,则这个数称的次方根。即若,则称的次方根,,
1)当为奇数时,次方根记作;
2)当为偶数时,负数没有次方根,而正数有两个次方根且互为相反数,记作。
②性质:1);2)当为奇数时,;
3)当为偶数时,。
(2)幂的有关概念 ( )
①规定:1)
3);(4)、N* 且。
②性质:1)、Q);
2)、Q);
3)Q)。
(注)上述性质对r、R均适用。
(3)对数的概念
①定义:如果的b次幂等于N,就是,那么数称以为底N的对数,记作其中称对数的底,N称真数。
1)以10为底的对数称常用对数,记作;
2)以无理数为底的对数称自然对数,,记作;
②基本性质:
1)真数N为正数(负数和零无对数);2);
3);4)对数恒等式:。
③运算性质:如果则
1);
2);
3)R)。
④换底公式:
1);2)。
2. 指数函数、对数函数、幂函数
(1)指数函数:
①定义:函数称指数函数,
1)函数的定义域为R;2)函数的值域为;
3)当时函数为减函数,当时函数为增函数。
②函数图像:
1)指数函数的图象都经过点(0,1),且图象都在第一、二象限;
2)指数函数都以轴为渐近线(当时,图象向左无限接近轴,当时,图象向右无限接近轴);
3)对于相同的,函数的图象关于轴对称。
③函数值的变化特征:
(2)对数函数:
①定义:函数称对数函数,
1)函数的定义域为;2)函数的值域为R;
3)当时函数为减函数,当时函数为增函数;
4)对数函数与指数函数互为反函数。
②函数图像:
1)对数函数的图象都经过点(0,1),且图象都在第一、四象限;
2)对数函数都以轴为渐近线(当时,图象向上无限接近轴;当时,图象向下无限接近轴);
3)对于相同的,函数的图象关于轴对称。
③函数值的变化特征:
(3)幂函数
y=xa(a为常数)是幂函数. 它在第一象限内的情况分为a>1,0<a<1;a<0三种情况,其中a>0时,y=xa,在(0,+∞)内为增函数;a<0时,y=xa,在(0,+∞)内为减函数。
a
【典型例题】
例1. (1)计算:;
(2)化简:。
解:(1)原式=
;
(2)原式=
。
点评:根式的化简求值问题就是将根式化成分数指数幂的形式,然后利用分数指数幂的运算性质求解,对化简求值的结果,一般用分数指数幂的形式保留;一般地进行指数幂运算时,化负指数为正指数,化根式为分数指数幂,化小数为分数运算,同时兼顾运算的顺序。
例2. 已知,求的值。
解:∵,
∴,
∴,
∴,
∴,
∴,
又∵,
∴。
点评:本题直接代入条件求解繁琐,故应先化简变形,创造条件简化运算。
例3. 计算
(1);(2);
(3)。
解:(1)原式
;
(2)原式
;
(3)分子=;
分母=;
原式=。
点评:这是一组很基本的对数运算的练习题,虽然在考试中这些运算要求并不高,但是数式运算是学习数学的基本功,通过这样的运算练习熟练掌握运算公式、法则,以及学习数式变换的各种技巧。
例4. (1).若logx=z,则x、y、z之间满足
A. y7=xz B. y=x7z C.y=7xz D.y=zx
解:由logx=zxz=x7z=y,即y=x7z.
答案:B
(2)(2006辽宁 文13)方程的解为 。
解:考查对数运算。原方程变形为,即,得。且有。从而结果为。
点评:关于含指数式、对数式等式的形式,解题思路是转化为不含指数、对数式的普通等式或方程的形式,再来求解。
例5. 下列函数中值域为正实数的是
A. y=-5x B.y=()1-xI C.y= D.y=
解:∵y=()x的值域是正实数,而1-x∈R,∴y=()1-x的值域是正实数.
答案:B
例6. 已知f(x)的定义域为[0,1],则函数y=f[log(3-x)]的定义域是__________.
解:由0≤log(3-x)≤1
log1≤log(3-x)≤log
≤3-x≤12≤x≤.
答案:[2,]
例7.(1)(2004年湖北,文5)若函数y=ax+b-1(a>0且a≠1)的图象经过二、三、四象限,则一定有
A. 0<a<1且b>0 B.a>1且b>0
C. 0<a<1且b<0 D.a>1且b<0
解:作函数y=ax+b-1的图象.
答案:C
(2)(2004年全国Ⅱ,理6)函数y=-ex的图象
A. 与y=ex的图象关于y轴对称 B.与y=ex的图象关于坐标原点对称
C.与y=e-x的图象关于y轴对称 D.与y=e-x的图象关于坐标原点对称
解:图象法.
答案:D
例8. 函数y=()的递增区间是___________.
解:∵y=()x在(-∞,+∞)上是减函数,
而函数y=x2-2x+2=(x-1)2+1的递减区间是(-∞,1),∴原函数的递增区间是(-∞,1).
答案:(-∞,1)
例9. (1) 下图是指数函数(1)y=ax,(2)y=bx,(3)y=cx,(4)y=dx的图象,则a、b、c、d与1的大小关系是
A. a<b<1<c<d B.b<a<1<d<c
C. 1<a<b<c<d D.a<b<1<d<c
剖析:可先分两类,即(3)(4)的底数一定大于1,(1)(2)的底数小于1,然后再从(3)(4)中比较c、d的大小,从(1)(2)中比较a、b的大小.
解法一:当指数函数的底数大于1时,图象上升,且当底数越大,图象向上越靠近于y轴;当底数大于0小于1时,图象下降,底数越小,图象向右越靠近于x轴.得b<a<1<d<c.
解法二:令x=1,由图知c1>d1>a1>b1,
∴b<a<1<d<c.
答案:B
(2)已知函数f(x)=则f(2+log23)的值为
A. B. C. D.
解:∵3<2+log23<4,3+log23>4,
∴f(2+log23)=f(3+log23)=()3+log23=.
答案:D
例10. 已知函数为常数)
(1)求函数f(x)的定义域;
(2)若a=2,试根据单调性定义确定函数f(x)的单调性。
(3)若函数y=f(x)是增函数,求a的取值范围。
解:(1)由
∵a>0,x≥0
∴f(x)的定义域是。
(2)若a=2,则
设, 则
故f(x)为增函数。
(3)设
①
∵f(x)是增函数,
∴f(x1)>f(x2)
即 ②
联立①、②知a>1,
∴a∈(1,+∞)。
点评:该题属于纯粹的研究复合对数函数性质的问题,我们抓住对数函数的特点,结合一般函数求定义域、单调性的解题思路,对“路”处理即可。
【模拟试题】
1. 下列各式中成立的一项是( )
A. B.
C. D.
2. 化简的结果为( )
A. B. C. D.
3. 设指数函数,则下列等式中不正确的是 ( )
A. f(x+y)=f(x)·f(y) B.
C. D.
4. 若指数函数在[-1,1]上的最大值与最小值的差是1,则底数a等于 ( )
A. B. C. D.
5. 当时,函数和的图象只可能是( )
6. 函数的值域是( )
A. B. C. D. R
7. 函数,满足的的取值范围( )
A. B.
C. D.
8. 函数的单调递增区间是( )
A. B. C. D.
9. 函数(为常数),若时,恒成立,则
A. B. C. D.
10. 若,当时,的大小关系为
A. B. C. D.
11. (04年全国卷一.文2)已知函数
A. B. - C. 2 D. -2
12. 设( )
A. 0 B. 1 C. 2 D. 3
13. 若函数的图象与x轴有公共点,则m的取值范围是( )
A. m≤-1 B. -1≤m<0 C. m≥1 D. 0<m≤1
14. 函数的定义域是( )
A. B. C. D.
15. (2006湖北)设f(x)=,则的定义域为( )
A. B. (-4,-1)(1,4)
C. (-2,-1)(1,2) D. (-4,-2)(2,4)
16. 已知函数f (x)的定义域是(1,2),则函数的定义域是 .
17. 当a>0且a≠1时,函数f (x)=ax-2-3必过定点 .
18. 已知-1<a<0,则三个数由小到大的顺序是
19. 求的定义域
【试题答案】
1~5 DCDDA 6~10 ADDAB 11. B
12. 解:C;,。
13. 解:,
画图象可知-1≤m<0。
答案为B。
14. D
15. B.
14与15提示:求函数的定义域就是求使解析式有意义的自变量的取值范围,在对数函数中只有真数大于零时才有意义。对于抽象函数的处理要注意对应法则的对应关系。
16. (0,1); 17.(2,-2); 18.;
19. 当;当
 爱华网
爱华网