到了一年级下学期,孩子们正式碰到数学问题。按照以前的课标来说,就是数学应用题,而现在我们数学的新课标不再说数学应用题,而说解决问题。按理来说,部分孩子就是因为数学问题理解不了,解决不了,导致数学学习上受阻碍,也有部分同学因为一开始没有引导好分析问题的思路,结果从此数学学得一塌糊涂。
对于这个问题,我先从一年级上学期说起。
一年级上册,解决问题的雏形往往在课本练习的安排中占据了重要的位置,主要的类型是“看图列式”,通过看图列式的类型,让孩子了解小学数学解决问题的雏形,对于孩子们进一步熟悉解决问题打下良好的基础。而正是“看图列式”题,让一部分孩子混淆了。综观一年级上册的看图列式题,不外乎有这两种类型:
类型一:是知道两个部分数,问号的指向性很强,要求“总数”,必须采用加法计算,列式:4 + 3 = 7(个)。引导孩子解决时,最好能让孩子自己口头叙述:“左边有4个○,右边有3个○,要求一共有多少个○?一共是指把左边和右边合起来,所以用加法计算。”
类型二:是知道一个部分数和一个总数,要求另一“部分数”,问号的指向性也很强,一般情况下得采用减法计算列式:7—4 = 3(个),不能列成7—3=4,或者3+4=7。引导孩子解决时,最好能让孩子自己口头叙述:“这里一共有7个○,右边有4个○,要求左边有几个○?这里知道了总数是7,其中一部分是4,求另一部分,应该用减法计算。”
在上学期,我也跟孩子们渗透了两条最常用的数量关系式:部分数+部分数=总数 总数—部分数=部分数
对于目前一年级下学期的孩子来说,孩子们必须了解:一般情况下,一个完备的数学问题必须包括两个已知条件和一个问题。下学期需要掌握的解决问题的类型题是在上学期的看图列式的基础上提出来的。
类型一:是给出条件问题完备的应用问题:
第一种引导:13个同学,是表示总人数;6人是表示捉的那一部分人;要求藏起来的那一部分,必须用减法计算。列式为13-6=7(人)。一般情况下不能列成13-7=6或者6+7=13。(这一种适合理解能力比较强的孩子。)
第二种引导:如果孩子还不能明白,还可以采用图式帮助孩子理解。回过来看看,就像类型二。(这种适合理解能力比较弱的孩子)
但这种画图的能力很重要,以后还会学习画线段图帮助解决数学问题。如果孩子能会,就最好了。
类型二:是给出明确的信息、数据,由学生提出问题后,理解意义进行计算。
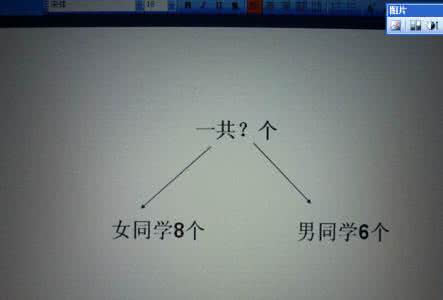
如:有8个女同学,有6个男同学。 一共有多少个同学?
第一步,学生要补充问题:“一共有多少个同学?”还可以补充为:女同学比男同学多几个?或者男同学比女同学多几个?(但这种比多比少的问题我们下几个单元才能学到)然后才分析问题并列式计算:8+6=14(个)或者6+8=14(个)
分析时,第一种引导:已经知道了8个女同学(部分数),6个男同学(部分数),要求一共有多少个同学,是求总数(从“一共”可以知道),所以用加法计算。
第二种引导:同样可以采用图式帮助孩子理解,像上学期学过的类型一。
你还能提出什么问题?完全由孩子观察图画,找出条件并提出问题。
可以提出这样的问题:
1、有9只黄鸭,4只白鸭,一共有多少只鸭?
9+4=13(只)
2、黄鸭和白鸭一共有13只,黄鸭有9只,白鸭有多少只?
13-9=4(只)
3、黄鸭和白鸭一共有13只,白鸭有4只,黄鸭有多少只?
13-4=9(只)
……
所以,从本周开始,让孩子写数学解决问题题,每周最少写2个,1个加法,1个减法,写在一个本子上,让小孩子当时我们家长的小老师,考考我们,作为家长可以适当答错,让孩子“指导”我们如何正确解决。就是想培养孩子善于观察生活,从生活中发现数学问题并解决数学问题的能力,培养孩子会说的能力。当然,数学要想学好,必须有阅读作基础。多阅读的孩子,数学的理解能力也相应比较强。而不爱阅读,少阅读的孩子,数学的理解能力也相应比较弱。所以,希望能多多培养孩子阅读的习惯。希望这篇文章对您有所帮助。谢谢阅看!
吴老师
附录:我来当当小老师,题目样版。
1、我家上面有8层楼,下面有2层楼,我们这幢房子一共有几层楼?
8+2+1=11(层)
2、妈妈买了32盒油画棒,有两种颜色,蓝色的有17盒,红色的有几盒?
32-17=15(盒)
3、妈妈下班买了20个苹果,爸爸吃了5个,我吃了2个,还剩下多少个?
20-5-2=13(个)
4、我的家里一共养了8只母鸡,别人送给我5只鸡,一共有几只鸡?
8+5=13(只)
 爱华网
爱华网