【方法归纳】
①直接法求三角形面积.如图所示,△ABC中AD为边BC上的高,则S△ABC=BC·AD.
②补全法求三角形面积.如图所示,S△ABC=S矩形BDFE- S△ABE- S△ACF- S△BCD.
③分割法求三角形面积.如图所示,S△ABC=S△ABD+S△ACD=AD·BF+AD·CE=AD·(BF+CE).
④平移法求三角形面积.如图所示,过点A作AD∥BC,则S△ABC=S△BCD.
当一个三角形(或其他多边形)的形状或大小发生变化时,产生面积变化.利用已知条件求出,变化过程中该三角形(或其他多边形)的面积.
【典型例题】
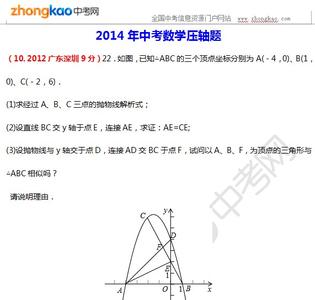
1.(13新疆)如图,已知抛物线y=ax2+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).
(1)求抛物线的解析式;
(2)在(1)中抛物线的对称轴上是否存在点D,使△BCD的周长最小?若存在,求出点D的坐标,若不存在,请说明理由;
(3)若点E是(1)中抛物线上的一个动点,且位于直线AC的下方,试求△ACE的最大面积及E点的坐标.
百度搜索“爱华网”,专业资料,生活学习,尽在爱华网!
 爱华网
爱华网