高中数学各年级学习内容及总结 一般第一学期讲必修1、2或1、4。必修1是整个高中的基础,一定要学扎实了。
时间就像牙膏,只要挤,总会有的
必修1共有三章内容两个模块
第一章集合与函数的概念
第二章基本初等函数
第三章函数的应用
两个模块:集合和函数。
建议10%的精力学集合90%的精力学函数
曾经辅导过一个高一的学生,那学生说他在原先的辅导里,那儿的老师集合就给他上了8次课,这真是让家长把钱往死里花呀。
今天先给大家分享一下集合的相关知识,总体而言这部分知识还是比较简单的,但是这部分知识出考题的特点是会与其他知识集合例如函数,不等式,方程等等。就集合本身的知识现简单列举如下(供大家参考):
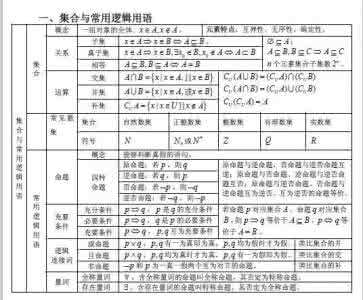
集合的概念(理解就行),集合元素的特点:确定性、互异性、无序性(重要考点,对互异性的考查最多),元素与集合关系:∈、?,常见数集符号:N、R、Q、Z、N+或N*(对于R和[size=16.363636016845703px]N*见的最多),集合的表示:列举法、描述法(今后见到的80%的题目都是描述法)。
集合间的关系:包含于、真包含于、不包含于、相等,子集、真子集、空集(重要考点)。若集合有n个元素则其具有2^n个子集(重要考点)。
集合间的运算:交、并、补(重要考点,每年高一期中期末及高考必考)。集合运算的性质(由于这里面敲公式不妨方便就不一一列举了)(重要考点),Veen图(用于解决集合运算问题的利器)。
时间就像牙膏,只要挤,总会有的
集合学完之后,就到了整个高中最核心、最重要、贯穿全程的知识——函数。函数真的有这么重要吗?下面我来和大家一起简单的分析一下:
必修2主要学两块内容:立体几何和直线与圆(解析几何初步)。在立体几何部分,将会遇到几何体的表面积,体积,各种空间角和距离等等问题的计算,一旦遇到了与之相关的求最大值,最小值的问题基本就要采用函数求最值的方法来解决。直线与圆的方程,直线方程这货一变形就是个函数。圆的方程经常和直线一起考,一联立变形,或者运用点到直线的距离公式等问题经常用到函数的相关知识。
必修3主要学两块内容:算法和概率统计。在算法中,会经常运用到函数的迭代思想。算法的核心部分循环体或分支结构,常以函数的形式出现。概率统计,高中阶段学习的概率统计问题尚未与函数有太紧密的联系,但是上过大学后这部分知识还是要与函数产生各种交集。
必修4主要学习三角函数和平面向量。三角函数,看到后两个字没,这货就是个函数,而且是非常重要的一个初等函数。现在的学生幸福多了,这部分内容比课改前容易了不少,余切,反三角函数,积化和差,和差化积等内容都删除了。平面向量,你抽空到图书馆看看必修4的课本,共有三章,1.三角函数,2.平面向量,3.三角恒等变形。看到没,这货放在两个三角函数内容之间,你要出跟他们没关系,鬼都不信。
必修5主要学习三块内容:解三角形,数列,不等式。解三角形,怎么解,想你们初中时的解直角三角形是怎么解的,主要是通过勾股定理再加上特殊角的三角函数或题中告知角的三角函数值集合起来求解。高中无非就是推广到了任意角的三角函数,然后再加上正余弦定理就可以解决了。初中时解这类问题,常用到方程的思想,高中同样解这类问题会常用到方程组的思想。数列,对于数列与函数的关系,有一种说法师这样来形容的,数列是定义域在正整数上面的函数。数列的内容除了基本的等差,等比,求通项,求和还有一类非常重要的问题就是数列相关的不等关系与最值问题,你在学习这部分内容的时候就会发现用处理函数问题的思想和方法来解决这些问题是如此的轻松惬意。不等式,很多不等式的问题你把他一变形,那就是一个函数。
时间就像牙膏,只要挤,总会有的 ////////新
重头戏来了,函数的学习将导致高中数学学习的分水岭。学的好的同学在后面学习中顺风顺水,学不好的同学将谈数学而色变。如何学好函数呢,要注意数形结合,认真研究函数图象,如果一个函数的图象搞清楚了,那么关于这个函数的所有问题就基本都搞清楚了。
函数这个概念比较抽象,初中主要是运用变量来定义函数,而高中则是在集合的基础上进行定义的相比之下更严格,更抽象。关于函数的定义我想写这样一句话,非空数集的映射就是函数。如果你能看懂了,说明函数的概念你就学习的差不多了。关于函数概念的学习我想主要从三方面入手:①集合的对应;②关系式;③图像。要分别会举出正例和反例。关于函数的三要素:定义域、对应关系、值域都是重要考点。定义域即自变量的取值范围,要养成一个习惯,看到一个函数先求它的定义域。求函数的定义域要注意:①分母不等于0;②偶次方根内被开方数非负;③对数的底数大于0且不等于1,真数大于0;④0指数幂的底数不为0;⑤实际问题的限制(例如买篮球的个数,自变量必须是自然数)。求函数的解析式主要方法有:①待定系数法;②换元法;③凑配法;④构造方程组法;⑤赋值法;⑥图像变换法(平移,对称)。求函数的值域主要方法有:①直接观察法;②配方法;③判别式法;④换元法;⑤单调性法;⑥不等式法;⑦分离常数法;⑧数形结合法。总结:函数的定义域与解析求法比较简单,值域相对来讲方法较多,需要较灵活的运用所学知识,有一定难度。
函数的基本性质:①单调性(核心性质);②奇偶性(先看定义域是否关于原点对称);③周期性(主要放在三角函数部分来讲)
重要的初等函数:一次函数,反比例函数,二次函数,指数函数(底大图高),对数函数(底大图右),幂函数(重点掌握三次函数与1/2次函数的图像与性质)。关于初等函数怎么学习呢,初期一定要注意多画图象,反复研究函数的性质。
 爱华网
爱华网