几何型综合问题一般会先给定几何图形,如等腰三角形、直角三角形、菱形、矩形、正方形、梯形等,然后根据已知条件进行计算,有动点运动,对应产生线段、面积等变化,求对应的(未知)函数的解析式(即在没有求出之前不知道函数解析式的形式是什么)和求函数的定义域,最后根据所求的函数关系进行探索研究。
对于几何型综合问题我们一定要清楚在什么条件下图形问题,如满足什么样条件相似等或探究线段之间的位置关系等,在求面积问题时相应x的值是否满足一定关系等。
在很多几何型综合问题都会求函数解析式,而求函数解析式的关键是列出变量之间的等量关系,变形写成y=f(x)的形式。一般有直接法(直接列出含有x和y的方程)和复合法(列出含有x和y和第三个变量的方程,然后求出第三个变量和x之间的函数关系式,代入消去第三个变量,得到y=f(x)的形式),当然还有参数法,这个已超出中考数学要求。
找等量关系的途径在初中主要有利用勾股定理、平行线截得比例线段、三角形相似、面积相等方法。求定义域主要是寻找图形的特殊位置和根据解析式求解。而最后的探索问题千变万化,但少不了对图形的分析和研究,用几何和代数的方法求出x的值。几何型综合题一般做为压轴题出现,一般分三小题呈现。
在解数学综合题时我们要做到:数形结合记心头,大题分小题来转化,潜在条件不能忘,化动为静多画图,分类讨论要严密,方程函数是工具,计算推理要严谨。
典型例题1:
解题反思:
考查了二次函数综合题:熟练掌握用待定系数法求二次函数解析式、二次函数的性质和对称的判定与性质;理解坐标与图形性质,会利用两点间的距离公式计算线段的长;掌握线段垂直平分线的判定方法和平行四边形的性质;会利用相似比计算线段的长.
典型例题2:
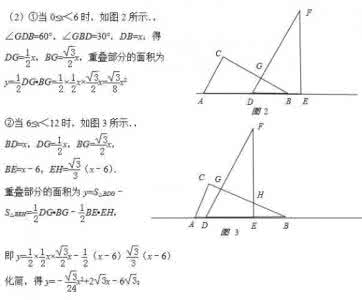
解题反思: 本题考查了几何变换综合题,(1)利用了锐角三角函数,矩形的性质;(2)利用面积的和差,分类讨论时解题关键,以防遗漏;(3)利用了垂线段最短的性质,三角形的中位线定理,锐角三角函数.
【作者:吴国平】
 爱华网
爱华网