圆锥曲线方程及性质
椭圆、双曲线、抛物线的定义、标准方程、几何性质及其应用
二. 课标要求:
1. 了解圆锥曲线的实际背景,感受圆锥曲线在刻画现实世界和解决实际问题中的作用;
2. 经历从具体情境中抽象出椭圆、双曲线模型的过程,掌握它们的定义、标准方程、几何图形及简单性质;
3. 了解抛物线的定义、几何图形和标准方程,知道抛物线的有关性质。
三. 命题走向:
本讲内容是圆锥曲线的基础内容,也是高考重点考查的内容,在每年的高考试卷中一般有2~3道客观题,难度上易、中、难三档题都有,主要考查的内容是圆锥曲线的概念和性质,从近十年高考试题看主要考查圆锥曲线的概念和性质。圆锥曲线在高考试题中占有稳定的较大的比例,且选择题、填空题和解答题都涉及到,客观题主要考查圆锥曲线的基本概念、标准方程及几何性质等基础知识和处理有关问题的基本技能、基本方法。
【教学过程】
基本知识要点回顾:
1. 椭圆
(1)椭圆概念
平面内与两个定点、的距离的和等于常数(大于)的点的轨迹叫做椭圆。这两个定点叫做椭圆的焦点,两焦点的距离叫椭圆的焦距。若为椭圆上任意一点,则有。
椭圆的标准方程为:()(焦点在x轴上)或()(焦点在y轴上)。
注:①以上方程中的大小,其中;
②在和两个方程中都有的条件,要分清焦点的位置,只要看和的分母的大小。例如椭圆(,,)当时表示焦点在轴上的椭圆;当时表示焦点在轴上的椭圆。
(2)椭圆的性质
①范围:由标准方程知,,说明椭圆位于直线,所围成的矩形里;
②对称性:在曲线方程里,若以代替方程不变,所以若点在曲线上时,点也在曲线上,所以曲线关于轴对称,同理,以代替方程不变,则曲线关于轴对称。若同时以代替,代替方程也不变,则曲线关于原点对称。
所以,椭圆关于轴、轴和原点对称。这时,坐标轴是椭圆的对称轴,原点是对称中心,椭圆的对称中心叫椭圆的中心;
③顶点:确定曲线在坐标系中的位置,常需要求出曲线与轴、轴的交点坐标。在椭圆的标准方程中,令,得,则,是椭圆与轴的两个交点。同理令得,即,是椭圆与轴的两个交点。
所以,椭圆与坐标轴的交点有四个,这四个交点叫做椭圆的顶点。
同时,线段、分别叫做椭圆的长轴和短轴,它们的长分别为和,和分别叫做椭圆的长半轴长和短半轴长。
由椭圆的对称性知:椭圆的短轴端点到焦点的距离为;在中,,,,且,即;
④离心率:椭圆的焦距与长轴的比叫椭圆的离心率。∵,∴,且越接近,就越接近,从而就越小,对应的椭圆越扁;反之,越接近于,就越接近于,从而越接近于,这时椭圆越接近于圆。当且仅当时,,两焦点重合,图形变为圆,方程为。
2. 双曲线
(1)双曲线的概念
平面上与两点距离的差的绝对值为非零常数的动点轨迹是双曲线()*。
注意:①(*)式中是差的绝对值,在条件下;时为双曲线的一支(含的一支);时为双曲线的另一支(含的一支);②当时,表示两条射线;③当时,不表示任何图形;④两定点叫做双曲线的焦点,叫做焦距。
椭圆和双曲线比较:
椭圆
双曲线
定义
方程
焦点
注意:如何由方程确定焦点的位置!
(2)双曲线的性质
①范围:从标准方程,看出曲线在坐标系中的范围:双曲线在两条直线的外侧。即,即双曲线在两条直线的外侧。
②对称性:双曲线关于每个坐标轴和原点都是对称的,这时,坐标轴是双曲线的对称轴,原点是双曲线的对称中心,双曲线的对称中心叫做双曲线的中心。
③顶点:双曲线和对称轴的交点叫做双曲线的顶点。在双曲线的方程里,对称轴是轴,所以令得,因此双曲线和轴有两个交点,它们是双曲线的顶点。
令,没有实根,因此双曲线和y轴没有交点。
<1>注意:双曲线的顶点只有两个,这是与椭圆不同的(椭圆有四个顶点),双曲线的顶点分别是实轴的两个端点。
<2>实轴:线段叫做双曲线的实轴,它的长等于叫做双曲线的实半轴长。虚轴:线段叫做双曲线的虚轴,它的长等于叫做双曲线的虚半轴长。
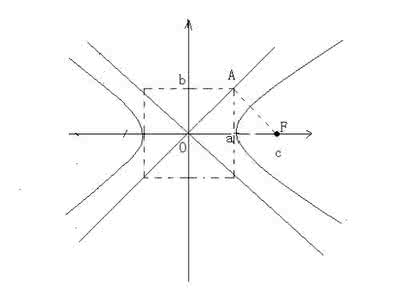
④渐近线:注意到所画的矩形,矩形确定了两条对角线,这两条直线即称为双曲线的渐近线。从图上看,双曲线的各支向外延伸时,与这两条直线逐渐接近。
⑤等轴双曲线:
<1>定义:实轴和虚轴等长的双曲线叫做等轴双曲线。定义式:;
<2>等轴双曲线的性质:(1)渐近线方程为:;(2)渐近线互相垂直。
注意以上几个性质与定义式彼此等价。亦即若题目中出现上述其一,即可推知双曲线为等轴双曲线,同时其他几个亦成立。
<3>注意到等轴双曲线的特征,则等轴双曲线可以设为:,当时交点在轴,当时焦点在轴上。
⑥注意与的区别:三个量中不同(互换)相同,还有焦点所在的坐标轴也变了。
3. 抛物线
(1)抛物线的概念
平面内与一定点F和一条定直线l的距离相等的点的轨迹叫做抛物线(定点F不在定直线l上)。定点F叫做抛物线的焦点,定直线l叫做抛物线的准线。
方程叫做抛物线的标准方程。
注意:它表示的抛物线的焦点在x轴的正半轴上,焦点坐标是F(,0),它的准线方程是;
(2)抛物线的性质
一条抛物线,由于它在坐标系的位置不同,方程也不同,有四种不同的情况,所以抛物线的标准方程还有其他几种形式:,,.这四种抛物线的图形、标准方程、焦点坐标以及准线方程如下表:
标准方程
图形
焦点坐标
准线方程
范围
对称性
轴
轴
轴
轴
顶点
离心率
说明:(1)通径:过抛物线的焦点且垂直于对称轴的弦称为通径;(2)抛物线的几何性质的特点:有一个顶点,一个焦点,一条准线,一条对称轴,无对称中心,没有渐近线;(3)注意强调的几何意义:是焦点到准线的距离。
【典型例题】
例1. 求适合下列条件的椭圆的标准方程:
(1)两个焦点的坐标分别是、,椭圆上一点到两焦点距离的和等于;
(2)两个焦点的坐标分别是、,并且椭圆经过点;
(3)焦点在轴上,,;
(4)焦点在轴上,,且过点;
(5)焦距为,;
(6)椭圆经过两点,。
解:(1)∵椭圆的焦点在轴上,故设椭圆的标准方程为(),
∵,,∴,
所以,椭圆的标准方程为。
(2)∵椭圆焦点在轴上,故设椭圆的标准方程为(),
由椭圆的定义知,
,
∴,又∵,∴,
所以,椭圆的标准方程为。
(3)∵,∴,①
又由代入①得,
∴,∴,又∵焦点在轴上,
所以,椭圆的标准方程为。
(4)设椭圆方程为,
∴,∴,
又∵,∴,
所以,椭圆的标准方程为。
(5)∵焦距为,∴,
∴,又∵,∴,,
所以,椭圆的标准方程为或。
(6)设椭圆方程为(),
由得,
所以,椭圆方程为。
点评:求椭圆的方程首先清楚椭圆的定义,还要知道椭圆中一些几何要素与椭圆方程间的关系。
例2. (06山东)已知椭圆中心在原点,一个焦点为F(-2,0),且长轴长是短轴长的2倍,则该椭圆的标准方程是 。
解:已知为所求;
点评:求椭圆方程的题目属于中低档题目,掌握好基础知识就可以。
例3. (1998全国理,2)椭圆=1的焦点为F1和F2,点P在椭圆上.如果线段PF1的中点在y轴上,那么|PF1|是|PF2|的( )
A. 7倍 B. 5倍 C. 4倍 D. 3倍
解:不妨设F1(-3,0),F2(3,0)由条件得P(3,±),即|PF2|=,|PF1|=,因此|PF1|=7|PF2|,故选A。
点评:本题主要考查椭圆的定义及数形结合思想,具有较强的思辨性,是高考命题的方向。
例4. (1)已知焦点,双曲线上的一点到的距离差的绝对值等于,求双曲线的标准方程;
(2)求与椭圆共焦点且过点的双曲线的方程;
(3)已知双曲线的焦点在轴上,并且双曲线上两点坐标分别为,求双曲线的标准方程。
解:(1)因为双曲线的焦点在轴上,所以设它的标准方程为,
∵,∴,∴。
所以所求双曲线的方程为;
(2)椭圆的焦点为,可以设双曲线的方程为,则。
又∵过点,∴。
综上得,,所以。
点评:双曲线的定义;方程确定焦点的方法;基本量之间的关系。
(3)因为双曲线的焦点在轴上,所以设所求双曲线的标准方程为①;∵点在双曲线上,∴点的坐标适合方程①。
将分别代入方程①中,得方程组:
将和看作整体,解得,∴即双曲线的标准方程为。
点评:本题只要解得即可得到双曲线的方程,没有必要求出的值;在求解的过程中也可以用换元思想,可能会看的更清楚。
例5. (06上海卷)已知双曲线中心在原点,一个顶点的坐标为,且焦距与虚轴长之比为,则双曲线的标准方程是____________________.
解:双曲线中心在原点,一个顶点的坐标为,则焦点在x轴上,且a=3,焦距与虚轴长之比为,即,解得,则双曲线的标准方程是;
点评:本题主要考查双曲线的基础知识以及综合运用知识解决问题的能力。充分挖掘双曲线几何性质,数形结合,更为直观简捷。
例6. (1)(06福建卷)已知双曲线(a>0,b>0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是( )
A. (-1,2) B. (1,2) C. [2,+∞] D. (2,+∞)
(2)(06湖南卷)过双曲线M:的左顶点A作斜率为1的直线,若与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是( )
A. B. C. D.
(3)(06陕西卷)已知双曲线-=1(a>)的两条渐近线的夹角为,则双曲线的离心率为( )
A. 2 B. C. D.
解:(1)双曲线的右焦点为F,若过点F且倾斜角为的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率,
∴ ≥,离心率e2=,∴ e≥2,选C。
(2)过双曲线的左顶点(1,0)作斜率为1的直线:y=x-1,若与双曲线的两条渐近线分别相交于点,联立方程组代入消元得,
∴ ,x1+x2=2x1x2,
又,则B为AC中点,2x1=1+x2,代入解得,
∴b2=9,双曲线的离心率e=,选A。
(3)双曲线(a>)的两条渐近线的夹角为,则,∴ a2=6,双曲线的离心率为,选D。
点评:高考题以离心率为考查点的题目较多,主要实现三元素之间的关系。
例7. (1)(06江西卷)P是双曲线的右支上一点,M、N分别是圆(x+5)2+y2=4和(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为( )
A. 6 B. 7 C. 8 D. 9
(2)(06全国卷I)双曲线的虚轴长是实轴长的2倍,则
A. B. C. D.
解:(1)设双曲线的两个焦点分别是F1(-5,0)与F2(5,0),则这两点正好是两圆的圆心,当且仅当点P与M、F1三点共线以及P与N、F2三点共线时所求的值最大,此时|PM|-|PN|=(|PF1|-2)-(|PF2|-1)=10-1=9故选D。
(2)双曲线的虚轴长是实轴长的2倍,∴ m<0,且双曲线方程为,∴ m=,选A。
点评:关于双曲线渐近线、许多距离问题也是考查的重点。
例8. (1)焦点到准线的距离是2;
(2)已知抛物线的焦点坐标是F(0,2),求它的标准方程。
解:(1)y=4x,y=4x,x=4y,x=4y;
方程是x=8y。
点评:由于抛物线的标准方程有四种形式,且每一种形式中都只含一个系数p,因此只要给出确定p的一个条件,就可以求出抛物线的标准方程。当抛物线的焦点坐标或准线方程给定以后,它的标准方程就唯一确定了;若抛物线的焦点坐标或准线方程没有给定,则所求的标准方程就会有多解。
例9. (1)(06安徽卷)若抛物线的焦点与椭圆的右焦点重合,则的值为( )
A. B. C. D.
(2)(浙江卷)抛物线的准线方程是( )
(A) (B) (C) (D)
(3)(06上海春)抛物线的焦点坐标为( )
(A) (B) (C) (D)
解:(1)椭圆的右焦点为(2,0),所以抛物线的焦点为(2,0),则,故选D;
(2)2p=8,p=4,故准线方程为x=-2,选A;
(3)(直接计算法)因为p=2,所以抛物线y2=4x的焦点坐标为 。应选B。
点评:考查抛物线几何要素如焦点坐标、准线方程的题目根据定义直接计算即可。
例10. (1)(全国卷I)抛物线上的点到直线距离的最小值是( )
A. B. C. D.
(2)(2002全国文,16)对于顶点在原点的抛物线,给出下列条件:
①焦点在y轴上;
②焦点在x轴上;
③抛物线上横坐标为1的点到焦点的距离等于6;
④抛物线的通径的长为5;
⑤由原点向过焦点的某条直线作垂线,垂足坐标为(2,1)。能使这抛物线方程为y2=10x的条件是 . (要求填写合适条件的序号)
(3)(2001广东、河南,10)对于抛物线y2=4x上任意一点Q,点P(a,0)都满足|PQ|≥|a|,则a的取值范围是( )
A. (-∞,0) B. (-∞,2 C. [0,2] D. (0,2)
解:(1)设抛物线上一点为(m,-m2),该点到直线的距离为,当m=时,取得最小值为,选A
(2)从抛物线方程易得②,分别按条件③、④、⑤计算求抛物线方程,从而确定⑤。
(3)设点Q的坐标为(,y0),
由|PQ|≥|a|,得y02+(-a)2≥a2.
整理,得:y02(y02+16-8a)≥0,
∵y02≥0,∴y02+16-8a≥0.
即a≤2+恒成立.而2+的最小值为2.
∴a≤2.选B。
点评:抛物线问题多考查一些距离、最值及范围问题。
例11. (1)(07重庆文)已知以F1(2,0),F2(2,0)为焦点的椭圆与直线有且仅有一个交点,则椭圆的长轴长为
A. B. C. D.
(2)(07四川文)已知抛物线y=x2+3上存在关于直线x+y=0对称的相异两点A、B,则|AB|等于
A. 3 B. 4 C. 3 D. 4
解:(1)由直线与圆锥曲线相切△=0得关于a的方程,求得a=,故选C
(2)设直线的方程为,由,进而可求出的中点,又由在直线上可求出,∴,由弦长公式可求出。选C。
点评:(1)和(2)题都考查了直线与圆锥曲线的位置关系。
[思维小结]
在复习过程中抓住以下几点:
(1)坚持源于课本、高于课本,以考纲为纲的原则。高考命题的依据是《高考说明》。并明确考点及对知识点与能力的要求,其实质是精通课本,而本章考题大多数是课本的变式题,即源于课本,因此掌握双基、精通课本是关键;
(2)在注重解题方法、数学思想的应用的同时注意一些解题技巧,椭圆、双曲线、抛物线的定义揭示了各自存在的条件、性质及几何特征与圆锥曲线的焦点、焦半径、准线、离心率有关量的关系问题,若能用定义法,可避免繁琐的推理与运算;
(3)焦半径公式:抛物线上一点P(x1,y1),F为抛物线的焦点,对于四种抛物线的焦半径公式分别为(p>0):
【模拟试题】
一、选择题
1. 已知椭圆上的一点到椭圆一个焦点的距离为,则到另一焦点距离为( )
A. B. C. D.
2. 若椭圆的对称轴为坐标轴,长轴长与短轴长的和为,焦距为,则椭圆的方程为( )
A. B.
C或 D. 以上都不对
3. 动点到点及点的距离之差为,则点的轨迹是( )
A. 双曲线 B. 双曲线的一支 C. 两条射线 D. 一条射线
4. 设双曲线的半焦距为,两条准线间的距离为,且,那么双曲线的离心率等于( )
A. 2 B. 3 C. D.
5. 抛物线的焦点到准线的距离是( )
A. B. C. D.
6. 若抛物线上一点到其焦点的距离为,则点的坐标为( )。
A. B. C. D.
7. (07江苏理)在平面直角坐标系中,双曲线中心在原点,焦点在轴上,一条渐近线方程为,则它的离心率为
A. B. C. D.
8. (07福建理)以双曲线的右焦点为圆心,且与其渐近线相切的圆的方程是( )
A. B.
C. D.
9. 连接抛物线的焦点与点所得的线段与抛物线交于点,设点为坐标原点,则三角形的面积为( )
A. B. C. D.
10. 设椭圆的离心率为,右焦点为,方程的两个实根分别为和,则点( )
A. 必在圆上 B. 必在圆外
C. 必在圆内 D. 以上三种情形都有可能
二、填空题
1、若椭圆的离心率为,则它的长半轴长为______________。
2、双曲线的渐近线方程为,焦距为,这双曲线的方程为_____________。
3、若曲线表示双曲线,则的取值范围是 。
4、抛物线的准线方程为___________。
5、椭圆的一个焦点是,那么 。
6、(07江苏理)在平面直角坐标系中,已知顶点和,顶点在椭圆上,则 。
三、解答题
1. 为何值时,直线和曲线有两个公共点?有一个公共点?没有公共点?
2. 在抛物线上求一点,使这点到直线的距离最短。
3. 双曲线与椭圆有共同的焦点,点是双曲线的渐近线与椭圆的一个交点,求渐近线与椭圆的方程。
4. 若动点在曲线上变化,则的最大值为多少?
【试题答案】
一、选择题
1、D 点到椭圆的两个焦点的距离之和为
2、C
得,或
3、D ,在线段的延长线上
4、C
5、B ,而焦点到准线的距离是
6、C 点到其焦点的距离等于点到其准线的距离,得
7、A
8、A
9、B
10、C
二、填空题
1、 当时,;
当时,
2、 设双曲线的方程为,焦距
当时,;
当时,
3、
4、
5、 焦点在轴上,则
6、椭圆的定义和正弦定理的应用
三、解答题
1、解:由,得,即
当,即时,直线和曲线有两个公共点;
当,即时,直线和曲线有一个公共点;
当,即时,直线和曲线没有公共点。
2、解:设点,距离为,
当时,取得最小值,此时为所求的点。
3、解:由共同的焦点,可设椭圆方程为;
双曲线方程为,点在椭圆上,
双曲线过点的渐近线为,即
所以椭圆方程为;双曲线方程为
4、解:设点,
令,,对称轴
当时,;当时,
 爱华网
爱华网