黄金三角形
顶角为36°的等腰三角形其底与腰之比等于黄金比（设为ω;），这样的三角形叫黄金三角形，黄金三角形还有下列性质.
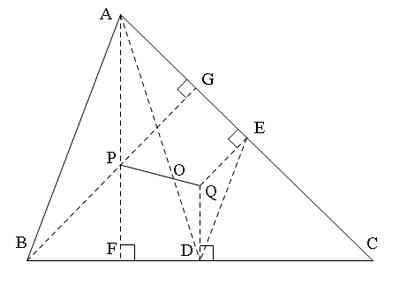
(1)如图1，BD为黄金三角形△ABC底角B的平分线，则△BCD也是黄金三角形；
(2)仿上作∠C的平分线交BD于E，则△CDE也是黄金三角形；如此下去可得一黄金三角形串：△1，△2, △3，…，△n, ……,且所有的黄金三角形相似，其相邻的两黄金三角形的相似比为ω;
(3)在上述的黄金三角形串△1，△2, △3，…，△n, …中，△n+3的右腰与△n的左腰平行（如图1中, △DEF的右腰DF与△ABC的左腰AB平行）
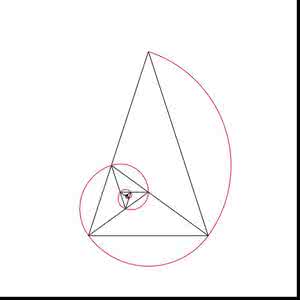
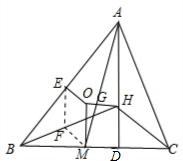
(4)三角形串中△n、△n+1、△n+3的底边上的三条高共点（如图2，△ABC、△BCD、△DEF底边上的高MN、NT、DN共点）；
与黄金三角形串﹛△n}相邻的均是些底角为36°的等腰三角形，他们也构成一三角形串，在这个三角形串中，相邻三个三角形底边上的高也构成黄金三角形（如图2，这个三角形串中的△DAB、△EBC、△FCD的高构成黄金三角形TMN）；这些黄金三角形也有一些有趣性质，这里就不一一列举了.
【金投手】：12.2黄金行情分析【基本面】美联储(FED)周三(12月1日)公布的经济褐皮书(Beige Book)显示，近几周美国经济继续缓慢复苏，制造业显示出的一些强势抵消了楼市"受压"以及雇主仍不愿招聘的影响。美联储的褐皮书进一步证明美国经
太阳金业：黄金的几种三角形态太阳金业集团主要从事现货黄金白银保证金交易经营，是香港金银业贸易场AA类会员112号行员。集团的分析师团队每日还会为客户提供贵金属市场资讯分析，为投资者提供专业的金市策略。形态学分析经常会利用三
原文地址：证明——三角形垂心重心外心共线欧拉线作者：微积猪我用了两年时间系统详细研究三角形，先后证明三角形三条角平分线交于一点（内心）、三边垂直平分线交于一点（外心）、三条中线交于一点（重心）、三条高交于一点（垂心）。证明这些，最终是要为
我用了两年时间系统详细研究三角形，先后证明三角形三条角平分线交于一点（内心）、三边垂直平分线交于一点（外心）、三条中线交于一点（重心）、三条高交于一点（垂心）。证明这些，最终是要为今天证明的这个命题做铺垫的。如果我都不能证有重心、垂心
九点共圆，指的是三角形中，三边的中点、三条高的垂足、垂心到三顶点连线的中点，这九个点分布在同一圆上。这个定理看起来是很不好证的 ，但是如果先不把九个点都考虑进来，只考虑一边中点、一个垂足、垂心到一顶点连线中点这三点共圆，那是肯
爱华网