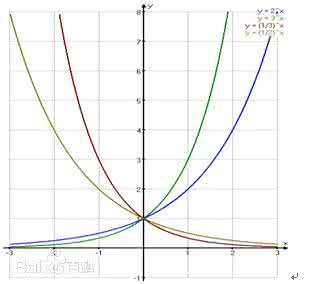
一、根式典型例题1:1、分数指数幂与根式的关系:分数指数幂与根式可以相互转化,通常利用分数指数幂的意义把根式的运算转化为幂的运算,从而简化计算过程.2、指数函数的单调性是由底数a的大小决定的,因此解题时通常对底数a按01进行分类讨论.1和a>二、有理数指数幂典型例题2:指数式的化简求值问题,要注意与其他代数式的化简规则相结合,遇到同底数幂相乘或相除,可依据同底数幂的运算规则进行,一般情况下,宜化负指数为正指数,化根式为分数指数幂.对于化简结果,形式力求统一.三、指数函数的图象和性质典型例题3:1、与指数函数有关的函数的图象的研究,往往利用相应指数函数的图象,通过平移、对称变换得到其图象.2、一些指数方程、不等式问题的求解,往往利用相应的指数型函数图象数形结合求解.求解与指数函数有关的复合函数问题,首先要熟知指数函数的定义域、值域、单调性等相关性质,其次要明确复合函数的构成,涉及值域、单调区间、最值等问题时,都要借助“同增异减”这一性质分析判断,最终将问题归纳为内层函数相关的问题加以解决.【作者:吴国平】
爱华网本文地址 » http://www.aihuau.com/a/389251/669362348197.html
更多阅读

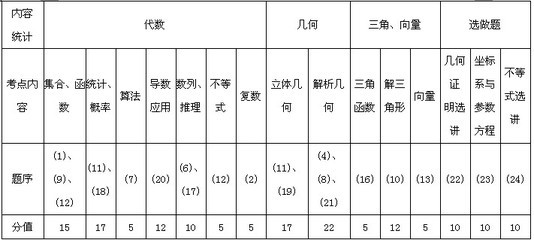
2013年高考数学试卷特点分析收集制作: 轻松愉快好心情一、以学生为主体,全面考察知识点。在2013年数学卷中,难易程度怎么样?我把试卷看了一遍,特别是看了全国试卷、某些省市的试卷,感觉今年试卷出的很好,突出了课标的要求,突出了以学生为主
2012年高考数学湖南卷试卷评析2012年高考数学湖南卷体现了普通高中数学课程标准的理念, 符合《普通高等学校招生全国统一考试大纲》和《普通高等学校统一考试湖南卷考试说明》(以下简称《考试说明》)的各项要求. 试卷全面考查了中学

2012年湖南省高考数学理科试题分析湖南省中小学教师继续教育指导中心 李再湘一、精彩点回放1.新题型闪亮登场。理科第16题考查在新环境下的创新意识,考查运算能力和创造性解决问题的能力。需要在学习中培养自己动脑的习惯,才可顺利

  高考数学二轮复习方法 首先,我们应当明确为什么要进行高考第二轮复习?也就是高考数学复习通常要分三轮(有的还是分四轮)完成,对于第二轮的目的和意义是什么呢?第一轮复习的目的是将我们学过的基础知识梳理和归纳,在这个

提高高考数学成绩的三大学习方法:一、思路思想提炼法:催生解题灵感“没有解题思想,就没有解题灵感。有了解题思想,解题思如泉涌。”但“解题思想”对很多学生来说是既熟悉又陌生。熟悉是因为教师每天挂在嘴边,陌生就是说不请它究竟是什

 爱华网
爱华网


