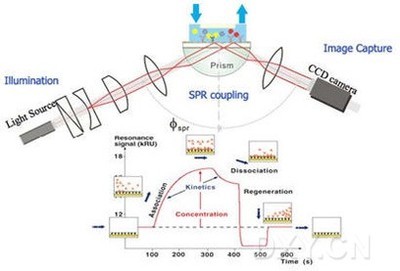
光 学
1.1 几何光学基础
1、光的直线传播:光在同一均匀介质中沿直线传播。
2、光的独立传播:几束光在交错时互不妨碍,仍按原来各自的方向传播。 3、光的反射定律:
①反射光线在入射光线和法线所决定平面内; ②反射光线和入射光线分居法线两侧; ③反射角等于入射角。 4、光的折射定律:
①折射光线在入射光线和法线所决定平面内;
②折射光线和入射光线分居法线两侧; S③入射角i1与折射角i2满足n1sini1?n2sini2;
④当光由光密介质向光疏介质中传播,且入射角大于临界
角C时,将发生全面反射现象(折射率为n1 的光密介质对折射率为n2的光疏介质的临界角
§1.2 光的反射
sinC?
n2
n1)。
S2
图1-2-1
1.2.1、组合平面镜成像:
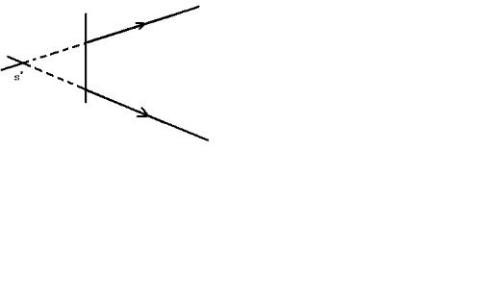
1.组合平面镜 由两个以上的平面镜组成的光学系统叫做组合平面镜,射向组合平面镜的光线往往要在平面镜之间发生多次反射,因而会出现生成复像的现象。先看一种较简单的现象,两面互相垂直的平面镜(交于O点)镜间放一点光源S(图1-2-1),S发出的光线经过两个平面镜反射后形成了S1、S2、
S3三个虚像。用几何的方法不难证明:这三个虚像都
位于以O为圆心、OS为半径的圆上,而且S和S1、S和
S2、S1和S3、S2和S3之间都以平面镜(或它们的延
长线)保持着对称关系。用这个方法我们可以容易地确定较复杂的情况中复像的个数和位置。
两面平面镜AO和BO成60o角放置(图1-2-2),用上述规律,很容易确定像的位置:①以O为圆心、OS为半径作圆;②过S做AO和BO的垂线与圆交于S1和S2;③过S1和S2作BO和AO的垂线与圆交于过3和S4作AO和BO的垂线与圆交于是在两平面镜中的5个像。
3
图1-2-2
S3和S4;④
S
S5,S1~S5便
双镜面反射。如图1-2-3,两镜面间夹角a=15o,OA=10cm,A点发出的垂直于L2的光线射向L1后在两镜间反复反射,直到光线平行于某一镜面射出,则从A点开始到最后一次反射点,光线所走的路程是多少?
L1
O
图1-2-3
A
L2
1P2是水平放置的米尺(有刻度的例1、如图1-2-6所示,AB表示一平直的平面镜,P
一面朝着平面镜),MN是屏,三者相互平行,屏MN上的ab表
示一条竖直的缝(即ab之间是透光的)。某人眼睛紧贴米尺上
的小孔S(其位置如图所示),可通过平面镜看到米尺的一部
分刻度。试在本题图上用三角板作图求出可看到的部位,并在P1P2上把这部分涂以标志。
2、全反射
全反射光从密度媒质1射向光疏媒质2,当入射角大于临
?1
A
图1-2-6
B
界角a?sinn21时,光线发生全反射。
全反射现象有重要的实用意义,如现代通讯的重要组成部分——光导纤维,就是利用光的全反射现象。图1-2-5是光导纤维的示意图。AB为其端面,纤维内芯材料的折射率
n1?1.3,外层材料的折射率n2?1.2,试问入射角在什么范围内才能确保光在光导纤维内
传播?
图1-2-5中的r表示光第一次折射的折射角,β表示光第二次的入射角,只要β大于临界角,光在内外两种材料的界面上发生全反射,光即可一直保持在纤维内芯里传播。
??sin?1n21
?1
n1.2?sin2?sin?1?67.40
n11.3?
r????90o?67.4o?22.6o
2
sini/sinr
图1-2-5
?1.3/1
o
sini?0.50,i?30只要即可。
例2、横截面为矩形的玻璃棒被弯成如图1-2-16所示的形状,一束平行光垂直地射入平表面A上。试确定通过表面A进入的光全部从表面B射出的R/d的最小值。已知玻璃的折射为1.5。
图1-2-16
例3. 普通光纤是一种可传输光的圆柱
形细丝,由具有圆形截面的纤芯A和包层B组成,B的折射率小于A的折射率,光纤的
端面与圆柱体的轴垂直,由一端面射入的光
在很长的光纤中传播时,在纤芯A和包层B的分界面上发生多次全反射。现在利用普通光纤测量流体F的折射率。实验方法如下:
图1-2-18 让光纤的一端(出射端)浸在流体F中。令
与光纤轴平行的单色平行光束经凸透镜折
射后会聚在光纤入射端面的中心O。经端面折射进入光纤,在光纤中传播。由于O点出发的光束为圆锥形,已知其边缘光线和轴的夹角为
a0,如图1-2-18所示。最后光从另一端面出
射进入流体F。在距出射端面h1处放置一垂直于光纤轴的毛玻璃屏D,在D上出现一圆形光斑,测出其直径为d1,然后移动光屏D至距光纤出射端面h2 处,再测出圆形光斑的直径
d2,如图1-2-19所示。
(1)若已知A和B的折射率分别为nA与nB。求被测流体F的折射率nF的表达式。 (2)若nA、nB和
a0均为未知量,如何通过进一步的实验以测出nF的值?
§1.3 光的折射
1.3.1、多层介质折射
如图:多层介质折射率分别为n1,n2,n3?则由折射定律得: n1sini1?n2sini2???nksinik
1.3.2、平面折射的视深
在水中深度为h处有一发光点Q,作OQ垂直于水面,求射出水面折射线的延长线与OQ交点Q?的深度h?与入射角i的关系。
设水相对于空气的折射率为
2
n1
3
n2
n3nR
n?
43。
图1-3-1
1.3.3、棱镜的折射与色散
入射光线经棱镜折射后改变了方向,出射光线与入射光线之间的夹角称为偏向角,由图1-3-4的几何关系知
DG
??i2?) ??(i1?i2)?(i1??? ?i1?i1
图1-3-4
??nsini1? 其中 sini1?nsini2 sini2
??i1?即 当i1,α很小时,i1?ni2,ni2
δ=(n-1)α
由于同一种介质对不同色光有不同的折射率,各种色光
的偏折角不同,所以白光经过棱镜折射后产生色散现象。虹
和霓是太阳被大气中的小水滴折射和反射形成的色散现象。
阳光在水滴上经两次折射和一次反射如图1-3-6。形成内紫
外红的虹;阳光经小滴两次折射和两次反射如图1-3-7,形成内红外紫的霓。由于霓经过多一次反射,因此光线较弱,不容易看到。
图1-3-7
1.3.4、费马原理
费马原理指出,光在指定的两点之间传播,实际的光程总是为最大或保持恒定,这里的光程是指光在某种均匀介质中通过的路程和该种媒质的折射率的乘积。
费马原理是几何光学中的一个十分重要的基本原理,从费马原理可以推导出几何光学中的很多重要规律。例如光的直线传播、反射定律,折射定律,都可以从光程极小推出。如果反射面是一个旋转椭球面,而点光源置于其一个焦点上,所有反射光线都经过另一个焦点,所有反射光线都经过另一个焦点,便是光程恒定的一个例子。此外,
透镜对光线的折射作用,也是很典型的。
一平凸透镜的折射率为n,放置在空气中,透镜面孔的半径为R。在透镜外主光轴上取一点F?,OF??f?(图1-3-8)。当平行光沿主光轴入射时,为使所有光线均会聚于F?
点。试问:透镜凸
图1-3-8
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网