nuomotu
诺模图
nomograph
根据一定的几何条件(如三点共线),把一个数学方程的几个变量之间的函数关系,画成相应的用具有刻度的直线或曲线表示的计算图表。是工程技术上常用的一种计算图表。诺模图使用方便,求解迅速,可以避免大量的重复计算,因此在机械设计中得到广泛的应用。诺模图的种类很多,有共线图和共点图(也称网络图)等。通常说的诺模图是指共线图。共线图的理论是由法国的M.de奥卡涅于1884年首先提出的。共线图是用 3个图尺表示一个包含3个变量的方程。在这些图尺上,凡是标值满足该方程的3个刻度点都必须位于同一直线上(图1[诺模图原理]、图2[=/cos 的诺模图]=/cos 的诺模图" class=image>)。其中最常用的是由 3条平行直线图尺组成的共线图,其典型方程为()+()=()。使用共线图时,如已知两个变量,则过该两变量的图尺上相应的变量点作一直线,该直线与第三图尺的交点就是所求第三变量的值。
诺模图的基本概念是图尺、图尺系数和图尺方程。
① 图尺:具有刻度的直线或曲线,其上注有按大小顺序排列的一组数字。图尺一般按变量的函数值来刻度,故又称函数图尺。函数图尺的刻度数字一般表示该变量的数值,例如图2 [=/cos 的诺模图]=/cos 的诺模图" class=image>中的Z尺是按lgZ刻度的,但标注的却是变量Z 的数值。
② 图尺系数:表示函数值单位的长度,记作 。以L表示直线图尺的长度,变量的标值范围从1到2,相应的函数值为(1)和(2),则图尺系数为=L/[|(2)-(1)|]。
③ 图尺方程:图尺上刻度所依据的方程式。若所画的函数为(),刻度的原点为()=0,从原点到任一刻度所量得的距离为,则图尺方程为=·()。因此图 1中的三平行尺共线图中三条图尺的方程分别为
u图尺 1=1()
v图尺 2=2()
w图尺 [543-01]
图尺距离 /=1/2
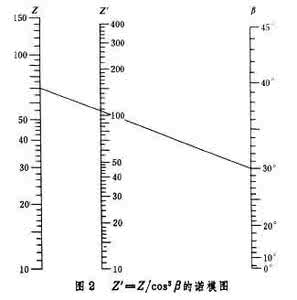
例如,绘制计算斜齿轮当量齿数公式Z=Z/cos(的共线图[=/cos 的诺模图]=/cos 的诺模图" class=image>),式中Z 为实际齿数, 为螺旋角。先将公式两边取对数,使它化为典型方程的形式,即
lgZ=lgZ-3lgcos
若常用齿数范围 Z=10~150,常用螺旋角范围=0°~45°,得出圆化值Z=10~400;取图尺长度L=120毫米,则图尺系数分别为
[544-01]
为刻度方便,取1=100, 2=250,得三条图尺的方程为
Z 图尺 1=11gZ=1001gZ
β图尺 2=2(-3lgcos)=-750lgcos
Z图尺 [544-02]
/=1/2=100/250=2/5
若选取+=105,则=30,=75。画出共线图(图2[=/cos 的诺模图]=/cos 的诺模图" class=image>)。
使用时,若已知Z=70,=30,则通过这两点作一直线,在与Z图尺的交点处读得Z=110。
参考书目
孟宪铎编著:《计算图原理和绘制方法》,机械工业出版社,北京,1981。
石光源
以上就是网友分享的关于"诺模图"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网

