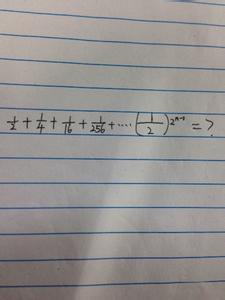数列求和不等式 放缩法证明数列不等式 数列求和不等式的证明策略

数列求和不等式的证明策略

一． 直接放缩型

11111(n2). 2n1n22n

111证明： (k=2n) 2nnkn1

111111111+, 2n2n2nn1n22nn1n1n11111n1, 即2n1n22nn1例1．求证：

例2. 设an11a1a1a,a2.求证：an2. 23n

解析 an11a1a1a1121212. 3n23n2

又k2kkk(k1),k2

1111， 2k(k1)k1kk

于是an11

212121(11)(11)(11)212. 23n223n1nn

二． 可放缩成等差数列型

n(n1)(n1)2

223n(n1).(nN) 例1．求证：22

证明：n(n1)n2n223n(n1)12n又n(n1)nn12n1 22n(n1)， 2

1n22n(n1)2

, 得证。 223n(n1)(352n1)=222

三． 可放缩成等比数列型

例1．数列{an}满足an+1=an2-nan+1(nN)，且ann+2求证：1111 1a11a21an2证明：an+1=an(an-n)+1an(n+2-n)+1=2an+1an+1+12(an+1) an+12(an-1+1) 即111112n1n1(a13) 1an2(an11)2(an21)2(a11)2

11111111123n1n1 1a11a21an222222

例2．已知f(x)=x2,x(0,)，数列{xn}满足xn+1=f(xn)(nN)，且x1=1，设an=|xn-2|，x1

Sn为{an}前n项和，证明：Sn<2。 2

证明an+1=|xn+1-2|=|xn2x22xn2|x2||=(21)n 2|=|n

xn1xn1|xn1|

又xn>0an+1<(21)|xn2|<(21)2|xn12|(21)n|x12|=(21)n1  Sn=a1+a2+an<(21)+(21)2(21)n =21

22[1(21)n]<21

222， 2

得证。

四． 可放缩成裂项差式型

例1．求证：1+

证明：1112 (nN) 22223n1111(n2) 2n(n1)n1nn

1+1111111111122. 222223n1nn23n

例2．求证：1+2

2232nn23 (n2,nN) 证明：n

n21nn2

nnnn

2(n1)nnn12(1

n11 =2

n(n1)(n1n)2(nn1)n(n1)n) 1+2

22332nn212(1121

21

31

n11

n)31

n3.

五． 两项配凑放缩型

例1．已知.xn=2+1

(2)n1

3，求证：(-1)x1+(-1)2x2+(-1)nxn<1 (nN)

证明：(-1)nxn=(-1)n2+112n(1)n3,

不妨考虑n为奇数时，(-1)nxn+(-1)n+1xn+1=

112

3

n

2

1

n1

13

=

2n2n12n2n111

nn1nn1

112222(2n)(2n1)

33

于是n为偶数时，(-1)x1+(-1)2x2+(-1)nxn<n为奇数时，前n-1项为偶数项，

1111

2n1n<1, 2222

于是有(-1)x1+(-1)2x2+(-1)nxn<1+(-1)nxn=1-xn=1-(2+

11

(2)n

3

)=-1+

112n

3

1,得证。

例2．已知an=

2n-21117[2+(-1)n-1] (nN)，证明：对任意的整数m>4，有 3a4a5am8

证明：由通项公式得a4=2，

32n12n211311

当n3且n为奇数时， []=

anan122n212n11222n32n12n21132n12n231

(), <=

22n22n1222n3

当m>4且m为偶数时，<

11111111

()() a4a5ama4a5a6am1am

131111311137

(34m2)(1m4), 222224288222

当m>4且m为奇数时，

11117111

,

amam18a4a5ama4a51117

。 a4a5am8

综上对任意整数m>4有

评析：由于通项中涉及有(-1)n这一符号法则，因此结合两项之和将其消去，再行放缩便能易于求和使问题得证。

六．利用题设结论 例1 已知不等式

1111

[log2n],nN,n2.[log2n]表示不超过log2n 的最大整23n2

数。设正数数列{an}满足：a1b(b0),an

求证an2b,n3. 2b[log2n]nan1,n2. nan1

简析 当n2时annan11nan111，即 nan1anan1an1n

nn111111 ). (akak1anan1nk2k2k

于是当n3时有111[log2n]anana122b. 2b[log2n]例2 已知a11,an1(111)a.(I)用数学归纳法证明an2(n2)；(II)对n2nnn2ln(1x)x对x0都成立，证明ane2（无理数e2.71828） 解析 (II)结合第(I)问结论及所给题设条件ln(1x)x（x0）的结构特征，可得放缩思路：an1(11111)anlnan1ln(12n)lnan 2nnn2nn2

1111lnan2n。于是lnan1lnan2n， nn2nn2n1

i1(lnai1lnai)i1n111()n111111(2i)lnanlna112n2.1nn2ii212 即lnanlna12ane2.

111)(an1) )anan11(1n(n1)n(n1)n(n1)

11ln(an11)ln(an1)ln(1).n(n1)n(n1)an1(1

[ln(ai11)ln(ai1)]i2i2n1n1 11ln(an1)ln(a21)11， i(i1)n即ln(an1)1ln3an3e1e2.

七．利用单调性放缩

2例1. 设数列an满足an1annan1nN，当a13时证明对所有n1, 有

(i)ann2；(ii)1111 1a11a21an2 解析 (i)用数学归纳法：当n1时显然成立，假设当nk时成立即akk2，则当

nk1时ak1ak(akk)1ak(k2k)1(k2)21k3，成立。 (ii)利用上述部分放缩的结论ak12ak1来放缩通项，可得ak112(ak1)ak12k1(a11)2k142k1

11()n

1121. 122i141211k1. ak12 i1n11aii1n

例2已知各项均为正数的数列{an}的前n项和满足Sn1，且6Sn(an1)(an2),nN*

（1）求{an}的通项公式；

（2）设数列{bn}满足an(2bn1)1，并记Tn为{bn}的前n项和，求证： 3Tn1log2(an3),nN* （Ⅰ）解：由a1S1(a11)(a12)，解得a1＝1或a1＝2，由假设a1＝S1＞1，因此a1＝2。 又由an+1＝Sn+1- Sn＝(an11)(an12)(an1)(an2)，

得an+1- an-3＝0或an+1＝-an

因an＞0，故an+1＝-an不成立，舍去。

因此an+1- an-3＝0。从而｛an｝是公差为3，首项为2的等差数列，故｛an｝的通项为an＝3n-2。 （Ⅱ）由an(2b1)1可解得

13nlogz； bzlogz1a3n1n

从而Tnb1b2bnlogz36

253n。 3n1

31616163n236因此3Tn1logz(an3)logz。 3n13n225

3n236令f(x),则 253n13n23

f(n1)3n23n3(3n3)3。 f(n)3n53n2(3n5)(3n2)23

因(3n3)2(3n5)(3n2)29n7＞0，故

f(n1)＞f(n).

特别的f(n)f(1)

27＞1。从而3Tn1log(an3)logf(n)＞0， 20

即3Tn1＞log2(an3)。

1a例15 数列xn由下列条件确定：x1a0，xn1（I）证明：对n2总x,nN．n2xn

有xna；(II)证明：对n2总有xnxn1（02年北京卷第（19）题）

1a

解析 构造函数f(x)x,易知f(x)在[a,)是增函数。

2x

当nk1时xk1xk

12

axk

在[a,)递增故xk1f(a)a. 

1a1a

 对(II)有xnxn1，构造函数xf(x)x,它在[a,)上是增函数，n2x2xn

故有xnxn1xnf(a)0，得证。 2xn

八．数学归纳法

武汉市教育科学研究院命制的“武汉市2005-2006学年高三年级二月调研测试”第22

题：已知函数f(x)是在(0,+)上每一点处可导的函数，若xf/(x)>f(x)在x>0上恒成立，1）略；2）求证：当x1>0,x2>0时有f(x1+x2)>f(x1)+f(x2)；3）已知不等式ln(1+x)<x在x>-1且x0时恒成立，求证：

111n222

. ln2ln3ln(n1)222

2(n1)(n2)23(n1)

1a

其中第3问给出的参考答案为：

由2)结论推广到一般有f(x1)+f(x2)+f(xn)<f(x1+x2+xn)(n2),设f(x)=xlnx，则在xi>0(i=1,n)时，有x1lnx1+x2lnx2+xnlnxn<(x1+x2+xn)ln(x1+x2+xn), 令xn=

1

,

(n1)2

1111111

1s<, n

222

1223n(n1)n123(n1)

记sn=x1+x2+xn=

又sn>

11111

, 2334(n1)(n2)2n2

(x1+x2+xn)ln(x1+x2+xn)

<(x1+x2+xn)ln(1-11111n)<-(x1x2xn)()=- n1n1n12n22(n1)(n2)111111nlnlnln原不等式成立。 2(n1)(n2)22223232(n1)2(n1)2

上述证法的技巧性太强，通过结论2）的推广，及sn的缩小与放大的同时运用，才使得

放缩的尺度恰如其分，笔者经过进一步研究，得出了以下简洁证法：

爱华网本文地址 » http://www.aihuau.com/a/392551/649941423506.html