课本中的例题与习题,都是通过筛选的题目的精华,在解题的思路和方法上具有典型性和代表性,在由知识转化为能力的过程中具有示范性和启发性.它们的解题方法和结论本身都具有广泛迁移的可能.近几年的中考题有许多植根于现行教材,在课本中寻找命题的生长点.因此,重视课本典型例习题的研究,用好、用活课本十分重要.下面以人教版八年级上册数学教材第十二章《轴对称》中一道例题来看这样一类试题。
例题再现:如图,要在燃气管道l上修建一个泵站,分别向两镇供气。泵站修在管道的什么地方,可使所用的输气管线最短?你可以在l上找几个点试一试,能发现什么规律?
此题就是利用对称作点B的对称点Bˊ,连接A Bˊ,再找到A Bˊ与l的交点即可。因为是典型的例题,解题过程就不在详述,我们把这类题不妨称为“建泵站问题”(有的教材上也叫“马饮水问题”)。以此题为命题的根源,在中考试题中屡见不鲜,下面就结合近两年中的部分地市的中考题,谈谈这类问题。
1.(2010年鄂州)如图,正方形OABC的边长为6,点A、C分别在x轴、y轴的正半轴上,点D(2,0)在OA上,P是OB上一动点,则PA+PD的最小值为( )
A.2 B. C.4 D.6
考点:正方形的性质;轴对称的性质;
两点之间线段最短;勾股定理等。
专题:计算题。
分析:根据正方形的对称性,连接CP,
当点P移动到CD与OB的交点处时PA+PD最小,即求CD的长。
解答:连接CP,由正方形的对称性可知PA=PC,
∴PA+PD=PC+PD
∴当点C、P、D在一条线上时PC+PD最小
连接CD,可知OD=2,OC=6,由勾股定理的CD=2
∴选A
点评:本题主要考察了正方形具有对称性,关键是找出什么时候PA+PD的值最小。
2、(2010年滨州市)如图,等边△ABC的边长为6,AD是边BC上的中线,M是AD上的动点,E是边AC上的一点,若AE=2,EM+CM的最小值为________。
考点:等边三角形的性质;轴对称的性质;
两点之间线段最短;勾股定理等。
专题:计算题。
分析:点E关于AD的对称点在AB上,再过点C作AB得垂线,构造直角三角形,利用勾股定理来解。
解答:作点E关于AD的对称点F在AB上,作CH⊥AB于点H,
可知AF=AE=2,AH=AB=3,
∴HF=1,可求CH=3
∴由勾股定理得CF=2,故填2。
点评:关键是通过轴对称把直线同侧的点转化为异侧的点。
3. (2010年东营市) 如图,已知二次函数的图象与坐标轴交于点A(-1, 0)和点B(0,-5).
(1)求该二次函数的解析式;
(2)已知该函数图象的对称轴上存在一点P,使得△ABP的周长最小.请求出点P的坐标.
考点:二次函数解析式;一次函数解析式;二元一次方程组;轴对称的性质;勾股定理;两点之间线段最短等。
专题:函数综合题。
解答:(1)根据题意,得
解得
∴二次函数的表达式为.
(2)令y=0,得二次函数的图象与x轴的另一个交点坐标C(5, 0).
由于P是对称轴上一点,
连结AB,由于,
要使△ABP的周长最小,只要最小.
由于点A与点C关于对称轴对称,连结BC交对称轴于点P,则= BP+PC =BC,根据两点之间,线段最短,可得的最小值为BC.
因而BC与对称轴的交点P就是所求的点.
设直线BC的解析式为,根据题意,可得解得
所以直线BC的解析式为.……………………9分
因此直线BC与对称轴的交点坐标是方程组的解,解得
所求的点P的坐标为(2,-3).
4. (2011年菏泽市)如图,抛物线y=x2+bx-2与x轴交于A,B两点,与y轴交于C点,且A(-1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断的形状,证明你的结论;
(3)点是x轴上的一个动点,当MC+MD的值最小时,求m的值.
解答:(1)把点A(-1,0)的坐标代入抛物线的解析式y=x2+bx-2,整理后解得,
所以抛物线的解析式为 . 顶点.
(2).,,.
是直角三角形.
(3)作出点关于轴的对称点,则,.连接交轴于点,
根据轴对称性及两点之间线段最短可知,的值最小.
设抛物线的对称轴交轴于点..
...
方法点拨:此类试题往往以角、三角形、菱形、矩形、正方形、梯形、圆、坐标轴、抛物线等为背景,但都有一个“轴对称性”的图形共同点,解题时只有从变化的背景中提取出“建泵站问题”的数学模型,再通过找定直线的对称点把同侧线段和转换为异侧线段和,利用“两点之间线段最短”,实现“折”转“直”即可解决。有时问题是求三角形周长或四边形周长的最小值,一般此时会含有定长的线段,依然可以转化为“建泵站问题”。
下面再给一些练习题:
1、如图,菱形ABCD中,∠BAD=600,M是AB的中点,P是对角线AC上的一个动点,若PM+PB的最小值是3,则AB长为________.
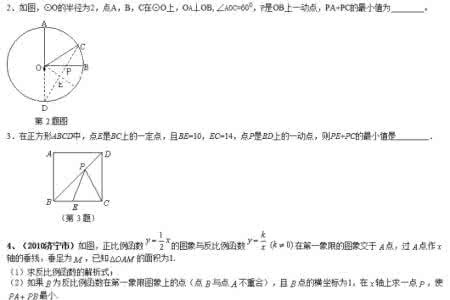
2、如图,⊙O的半径为2,点A,B,C在⊙O上,OA⊥OB,∠AOC=600,P是OB上一动点,PA+PC的最小值为________。
3.在正方形ABCD中,点E是BC上的一定点,且BE=10,EC=14,点P是BD上的一动点,则PE+PC的最小值是 .
4、(2010济宁市)如图,正比例函数的图象与反比例函数在第一象限的图象交于点,过点作轴的垂线,垂足为,已知的面积为1.
(1)求反比例函数的解析式;
(2)如果为反比例函数在第一象限图象上的点(点与点不重合),且点的横坐标为1,在轴上求一点,使最小.
5、(2011济宁市)去冬今春,济宁市遭遇了200年不遇的大旱,某乡镇为了解决抗旱问题,要在某河道建一座水泵站,分别向河的同一侧张村A和李村B送水。经实地勘查后,工程人员设计图纸时,以河道上的大桥O为坐标原点,以河道所在的直线为x轴建立直角坐标系(如图)。两村的坐标分别为A(2,3),B(12,7)。
(1)、若从节约经费考虑,水泵站建在距离大桥O多远的
地方可使所用输水管道最短?
(2)、(略)
练习题参考答案:
1、2;2、3;3、26;
4、(1)反比例函数的解析式为.(2)(2) 由 得 ∴为(,).
设点关于轴的对称点为,则点的坐标为(,).
令直线的解析式为.
∵为(,)∴∴
∴的解析式为.
当时,.∴点为(,).
5、解:(1)作点B关于x轴的对成点E,连接AE,则点E为(12,-7)
设直线AE的函数关系式为y=kx+b,则
2k+b=3
12k+b=-7
解得 k=-1
b=5
当y=0时, x=5
所以,水泵站建在距离大桥5千米的地方,可使所用输水管道最短。
教材是《课标》的载体,是课程目标和课程内容的具体化,是教与学的主要依据。中考数学试题大多来源于课本或从课本的基本要求出发加以拓宽,延伸和改造,所以在日常的教学中,教师不要盲目的甩开教材,滥用其他资料,而应高度重视课本上的一些典型例题和它们的解法,即“通用方法”的教学,在此基础上,还要充分引申、挖掘其蕴涵的深层潜力,做到“一题多解”、“一题多变”、“多题同法”,融会贯通,这样学生才会得心应手,才能有效地提高数学成绩。
2011-08-09 人教网
 爱华网
爱华网



