sanchuan leibi
三传类比
analogy between momentum,heat and mass transfer
指传递过程中的动量传递、热量传递和质量传递三者之间定量的类比关系。这三种传递过程有相同的传递机理,相同的数学表达形式。1874年O.雷诺首先指出热量与动量传递之间的类似性,并给出摩擦因子与传热分系数之间的定量关系。随后L.普朗特于1910年、G.I.泰勒于1916年和T.卡门于1939年相继对雷诺类比作了改进。有的提出了新的类比关系,并推广到动量传递和质量传递的类比。在类比关系的基础上,可以根据已知的一类传递规律,类推其他两种传递的规律。常见的类比关系有以下四种:
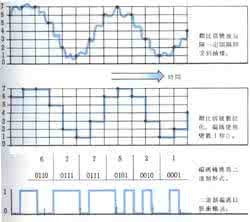
雷诺类比 雷诺假定单位时间内质量为的流体微团,从距壁面一定距离处向壁面运动,其流速由降为零。于是单位时间内失去的动量为,它等于壁面所受的剪切力,即:
=式中为壁面剪切应力;为壁面面积。又假定这一微团在距壁面同样距离处的温度为,达到壁面后其温度与壁温一致。所传递的热量为:
(-)=(-)式中为流体的定压比热容;为传热分系数。联立以上两式,得:
[547-01]由于[547-02],得:
[547-03]式中为流体密度;为范宁摩擦系数(见流动阻力)。比式即为雷诺类比的数学形式,表示传热分系数和范宁摩擦因子之间的定量关系。通常称为斯坦顿数:
[547-07]式中为雷诺数;为努塞尔数;为普朗特数[kg2]对于≈1的流体(如气体),则可简化成为:
[547-04]只要摩擦因子[kg1]和为已知,数和传热分系数即可推定。实验表明,对=1的流体,雷诺类比与湍流传热的数据颇为一致。
雷诺类比是以整个流场均为湍流的假设为基础,认为流体微团直接将热量带到了壁面,而忽略了近壁处存在层流底层。
普朗特类比 普朗特考虑到壁面附近有层流底层,流体到达层流底层后,不再以对流方式而以热传导方式进行传热。从这双层模型出发,导出的类比关系为:
[547-05]当=1时,此式简化成与雷诺类比关系相同。
卡门类比 卡门在前人的基础上提出一个三层模型,他认为,在湍流核心与层流底层之间还有一个过渡区。根据对数速度分布(见湍流),导出的类比关系为:
[547-06]普朗特和卡门类比式的适用范围都是Pr=0.7~20。
柯尔本类比 A.P.柯尔本应用管内湍流传热的经验式[kg1]=0.023范宁摩擦因子的经验式=0.046,得出关系式为:
[548-01]柯尔本将此式的左侧定义为传热因子,即:
[548-02]故称因子类比。将柯尔本类比用于传质过程,则有:
[548-03]式中为传质因子;为舍伍德数;为施密特数(见传质分系数);和[kg1]分别与传热过程的努塞尔数和普朗特数相对应上述其他三个类比应用于传质时,也有相对应的关系式。在=0.5~50的范围内因子经常用于关联传热、传质的实验数据。当出现边界层分离时,除了摩擦阻力外,还存在压差阻力(流动阻力),这时类比式不再适用,但和仍相等。
林纪方
以上就是网友分享的关于"三传类比"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网