大家知道,|a|的几何意义是:数轴上表示a的点到原点的距离;|a-b|的几何意义是:数轴上表示数a、b的两点的距离.对于某些问题用绝对值的几何意义来解,直观简捷,事半功倍.
一、求代数式的最值
例1 已知a是有理数,| a-2007|+| a-2008|的最小值是________..
解:由绝对值的几何意义知,| a-2007|+| a-2008|表示数轴上的一点到表示数2007和2008两点的距离的和,要使和最小,则这点必在2007~2008之间(包括这两个端点)取值(如图1所示),故| a-2007|+| a-2008|的最小值为1.
例2 |x-2|-| x-5| 的最大值是_______,最小值是_______.
解:把数轴上表示x的点记为P.由绝对值的几何意义知,|x-2|-| x-5|表示数轴上的一点到表示数2和5两点的距离的差,当P点在2的左边时,其差恒为-3;当P点在5的右边时,其差恒为3;当P点在2~5之间(包括这两个端点)时,其差在-3~3之间(包括这两个端点)(如图2所示),因此,|x-2|-| x-5|的最大值和最小值分别为3和-3.
二、解绝对值方程
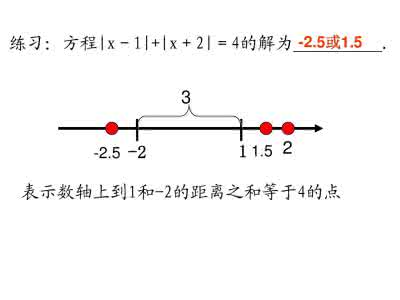
例3 方程|x-1|+|x+2|=4的解为__________.
解:把数轴上表示x的点记为P,由绝对值的几何意义知,当-2≤x≤1时,|x-1|+|x+2|恒有最小值3,所以要使|x-1|+|x+2|=4成立,则点P必在-2的左边或1的右边,且到表示数-2或1的点的距离均为个单位(如图3所示),故方程|x-1|+|x+2|=4的解为:
x =-2-=-,x = 1+= .
三、求字母的取值范
例4 若 |x+1|+|2-x|=3,则x的取值范围是________.
解:由绝对值的几何意义知,|x+1|+|x-2|的最小值为3,此时x在-1~2之间(包括两端点)取值(如图4所示),故x的取值范围是-1≤x≤2.
例5 对于任意数x,若不等式|x+2|+|x-4|>a恒成立,则a的取值范围是___________.
解:由绝对值的几何意义知,|x+2|+|x-4|的最小值为6,而对于任意数x,|x+2|+|x-4|>a恒成立,所以a的最值范围是a<6.
四、解不等式
例6 不等式|x+2|+|x-3|>5的解集是__________.
解:由绝对值的几何意义知,|x+2|+|x-3|的最小值为5,此时x在-2~3之间(包括两端点)取值,若|x+2|+|x-3|>5成立,则x必在-2的左边或3的右边取值(如图5所示),故原不等式的解集为x<-2或x>3.
五、判断方程根的个数
例7 方程|x+1|+|x+99|+|x+2|=1996共有( )个解.
A..4; B. 3; C. 2; D.1
解:当x在-99~-1之间(包括这两个端点)取值时,由绝对值的几何意义知,|x+1|+|x+99|=98,|x+2|<98.此时,|x+1|+|x+99|+|x+2|<1996,故|x+1|+|x+99|+|x+2|=1996时,x必在-99~-1之外取值,故方程有2个解,选(C).
六、综合应用
例8(第15届江苏省竞赛题,初一)已知|x+2|+|1-x|=9-|y-5|-|1+y|,求x+ y最大值与最小值.
解:原方程变形得|x+2|+|x-1|+|y-5|+|y+1||=9,
∵ |x+2|+|x-1|≥3,|y-5|+|y+1|≥6,
而|x+2|+|x-1|+|y-5|+|y+1|=9,
∴|x+2|+|x-1|=3,|y-5|+|y+1|=6,
∴-2≤x≤1,-1≤y≤5,
故x+ y的最大值与最小值分别为6和-3.
 爱华网
爱华网


