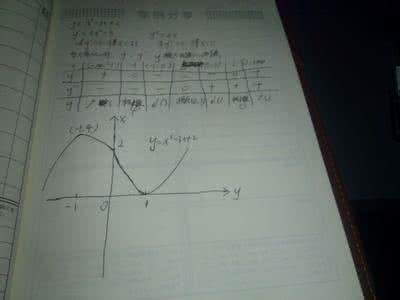
(Ⅰ)求b、c满足的约束条件,并在下面的坐标平面内,画出满足这些条件的点(b,c)的区域;
(Ⅱ)证明:-10≤f(x2)≤。 题型:解答题难度:中档来源:高考真题
(Ⅰ)解:,
依题意知,方程f′(x)=0有两个根x1、x2,且
等价于f′(-1)≥0,f(0)≤0,f′(1)≤0,f′(2)≥0,
由此得b、c满足的约束条件为,
满足这些条件的点(b,c)的区域为图中阴影部分,
(Ⅱ)由题设知,
故,
于是,
由于,而由(Ⅰ)知c≤0,故,
又由(Ⅰ)知-2≤c≤0,所以。
考点:
考点名称:简单线性规划问题(用平面区域表示二元一次不等式组)
二元一次不等式表示的平面区域:
二元一次不等式ax+by+c>0在平面直角坐标系中表示直线ax+by+c=0某一侧所有点组成的平面区域。不等式ax+by+c<0表示的是另一侧的平面区域。
线性约束条件:
关于x,y的一次不等式或方程组成的不等式组称为x,y的线性约束条件;
线性目标函数:
关于x、y的一次式欲达到最大值或最小值所涉及的变量x、y的解析式,叫做线性目标函数;
线性规划问题:
一般地,求线性目标函数在线性约束条件下的最大值或最小值问题称为线性规划问题。
可行解、可行域和最优解:
满足线性约束条件的解(x,y)称为可行解;由所有可行解组成的集合称为可行域; 使目标函数取得最大值或最小值的可行解叫做线性规划问题的最优解。
用一元一次不等式(组)表示平面区域:
(1)一般地,直线l:ax+by+c=0把直角坐标平面分成了三个部分:①直线l上的点(x,y)的坐标满足ax+by+c=0;②直线l一侧的平面区域内的点(x,y)的坐标满足ax+by+c>0;③直线l另一侧的平面区域内的点(x,y)的坐标满足ax+by+c<0.所以,只需在直线l的某一侧的平面区域内,任取一特殊点(x0,y0),从ax0+by0+c的值的正负,即可判断不等式表示的平面区域,可简称为,特殊点定域”.
(2)不等式组表示的平面区域是各个不等式所表示的平面区域的公共部分.
线性规划问题求解步骤:
(1)确定目标函数;
(2)作可行域;
(3)作基准线(z=0时的直线);
(4)平移找最优解;
(5)求最值。
线性规划求最值线性规划求最值问题:
(1)要充分理解目标函数的几何意义,诸如直线的截距、两点间的距离(或平方)、点到直线的距离、过已知两点的直线斜率等.
(2)求最优解的方法①将目标函数的直线平移,最先通过或最后通过的点为最优解,②利用围成可行域的直线的斜率来判断.若围成可行域的直线,且目标函数的斜率k满足的交点一般为最优解.在求最优解前,令z=0的目的是确定目标函数在可行域的什么位置有可行解,值得注意的是,有些问题中可能要求x,y∈N(即整点),它不一定在边界上.特别地,当表示线性目标函数的直线与可行域的某条边平行()时,其最优解可能有无数个,用图解法解决线性规划问题时,分析题目的已知条件,找出约束条件和目标函数是关键.可先将题目的量分类,列出表格,理清头绪,然后列出不等式组(方程组),寻求约束条件,并就题目所述找到目标函数.
线性规划的实际应用在线性规划的实际问题中:
主要掌握两种类型:
一、给定一定数量的人力、物力资源,问怎样运用这些资源能使完成的任务量最大,收到的效益最大;
二、给定一项任务,问怎样统筹安排,能使完成这项任务耗费的人力、物力资源最小.
(l)用图解法解决线性规划问题的一般步骤:①分析并将已知数据列出表格;②确定线性约束条件;③确定线性目标函数;④画出可行域;⑤利用线性目标函数(直线)求出最优解;⑥实际问题需要整数解时,应适当调整,以确定最优解.
(2)整数规划的求解,可以首先放松可行解必须为整数的要求,转化为线性规划求解,若所求得的最优解恰为整数,则该解即为整数规划的最优解;若所求得的最优解不是整数,则视所得非整数解的具体情况增加条件;若这两个子问题的最优解仍不是整数,再把每个问题继续分成两个子问题求解,……,直到求出整数最优解为止,
常见函数的导数:
(1)C′=0;(2);(3);(4);(5);(6);(7);(8)
导数的四则运算:
(1)和差:
(2)积:
(3)商:
复合函数的导数:
运算法则复合函数导数的运算法则为:
复合函数的求导的方法和步骤:
(1)分清复合函数的复合关系,选好中间变量;
(2)运用复合函数求导法则求复合函数的导数,注意分清每次是哪个变量对哪个变量求导数;
(3)根据基本函数的导数公式及导数的运算法则求出各函数的导数,并把中间变量换成自变量的函数。
求复合函数的导数一定要抓住“中间变量”这一关键环节,然后应用法则,由外向里一层层求导,注意不要漏层。
 爱华网
爱华网