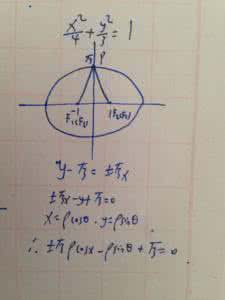
(1)求经过点F2且垂直地于直线AF1的直线l的参数方程;
(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,求直线AF2的极坐标方程.题型:解答题难度:中档来源:锦州三模
(1)圆锥曲线x=3cosθy=22sinθ化为普通方程x29+y28=1,
所以F1(-1,0),F2(1,0),则直线AF1的斜率k=33,
于是经过点F2垂直于直线AF1的直线l的斜率k1=-3,直线l的倾斜角是120°,
所以直线l的参数方程是x=1+tcos120°y=tsin120°(t为参数),
即x=-12t+1y=32t(t为参数).(6分)
(2)直线AF2的斜率k=-33,倾斜角是150°,
设P(ρ,θ)是直线AF2上任一点,
则ρsin30°=1sin(150°-θ),ρsin(150°-θ)=sin30°,(8分)
所以直线AF2的极坐标方程:3ρsinθ+ρcosθ=1.(10分)
考点:
考点名称:简单曲线的极坐标方程曲线的极坐标方程的定义:
一般地,在极坐标系中,如果平面曲线C上任意一点的极坐标中至少有一个满足方程f(ρ,θ)=0,并且坐标适合方程f(ρ,θ)=0的点都在曲线上,那么方程f(ρ,θ)=0叫做曲线C的极坐标方程。
求曲线的极坐标方程的常用方法:
直译法、待定系数法、相关点法等。
圆心为(α,β)(a>0),半径为a的圆的极坐标方程为,此圆过极点O。
直线的极坐标方程:
直线的极坐标方程是ρ=1/(2cosθ+4sinθ)。
圆的极坐标方程:
这是圆在极坐标系下的一般方程。过极点且半径为r的圆方程:考点名称:椭圆的参数方程
椭圆的参数方程:
椭圆的参数方程是,θ∈[0,2π)。
椭圆的参数方程的理解:
如图,以原点为圆心,分别以a,b(a>b>0)为半径作两个圆,点B是大圆半径OA与小圆的交点,过点A作AN⊥Ox,垂足为N,过点B作BM⊥AN,垂足为M,求当半径OA绕点O旋转时,点M的横坐标与点A的横坐标相同,点M的纵坐标与点B的纵坐标相同.而A、B的坐标可以通过引进参数建立联系.设,由已知得,即为点M的轨迹参数方程,消去参数得,即为点M的轨迹普通方程。
(1)参数方程,是椭圆的参数方程;
(2)在椭圆的参数方程中,常数a、b分别是椭圆的长半轴长和短半轴长.a>b,称为离心角,规定参数的取值范围是[0,2π);
(3)焦点在y轴的参数方程为
直线的参数方程:
过定点倾斜角为α的直线的参数方程为(t为参数)。
直线的参数方程及其推导过程:
设e是与直线l平行且方向向上(l的倾斜角不为0)或向右(l的倾斜角为0)的单位方向向量(单位长度与坐标轴的单位长度相同).直线l的倾斜角为α,定点M0、动点M的坐标分别为
直线的参数方程中参数t的几何意义是:表示参数t对应的点M到定点Mo的距离,当同向时,t取正数;当异向时,t取负数;当点M与Mo重合时,t=0.
 爱华网
爱华网