爱华网
放缩法证明数列不等式 放缩法证明数列不等式 破解数列型不等式“十一招”
更多阅读
n维向量数量积法证明柯西不等式 柯西不等式的证明方法
构造n维空间（可以超越三维，这里只是理论分析）其中有从原点O分别指向A、B两点的两个非零向量，分别记为a、bA点坐标为(a1,a2,a3,…,an)，B点坐标为(b1,b2,b3,…,bn)则向量a在第一维上的投影为a1
n维矢量和差法证明柯西不等式 柯西不等式向量证明
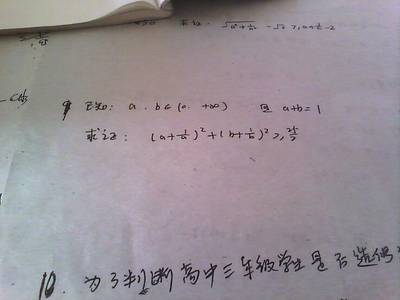
当我用两种方法证明了柯西不等式的时候，自然要寻求第三种方法。最终我发现，它是如此简单！只不过运用了平行四边形两邻边和大于任意一条对角线。建立一个n维空间（n可大于三，这里只是理论分析）其中有两个以原点为起点的矢量，分别为a、ba
用配方法证明代数式 用配方法证明
《用配方法证明》证明书用配方法证明设矩形长为x，那么宽为15-x面积S=x(15-x)=-x^2+15x=-(x-7.5)^2+56.25≤56.25所以面积最大为56.25平方米，无法达到60平方米x-12x+40=x-12x+36+4 =(x-6)^2+4因为(X-6)^2≥0所以(X-6)^2+4≥4所以大
如何证明均值不等式 均值不等式证明
《均值不等式证明》证明书均值不等式证明一、已知x,y为正实数，且x+y=1 求证xy+1/xy≥17/41=x+y≥2√(xy)得xy≤1/4而xy+1/xy≥2(散文阅读：www.sanwen.net )当且仅当xy=1/xy时取等也就是xy=1时画出xy+1/xy图像得01时，单调增
用向量法证明几何问题 用中间桥梁证明几何问题
初学几何的同学总感到证明题目太难了，苦于找不到证明方法，分析不清证明的途径，在几何教学中，我感觉重点应引导学生学会分析、解决问题的方法，教学活动是教学的教与学生的学的“双向”活动，教之以“鱼”授之以“渔”，教学的目的不在于“鱼”