玻恩-冯卡门边界条件 格林艾森常数 7个晶系 布洛赫定理
立方晶系的所有对称操作
一维、二维、三维情况下的电子态密度。 维格纳-赛茨元胞 电离能 价带 导带
石墨各化学键类型 色散关系 初基元胞
一维、二维、三维情况下的声子态密度。 能带 德拜模型 爱因斯坦模型 14种点阵 第一布里渊区 近自由电子近似 有效质量 紧束缚近似 亲和能 绝热近似
1、证明一维单原子链所有的独立模式构成正交完备集。 证
:
完备性自己补充
2、有N个相同原子组成的面积为S的二维晶格,证明在低温极限比热正比与T2。
证明:在k到k?dk间的独立振动模式对应于平面中半径n到n?dn间圆环的面积
L25
2?ndn,且2?ndn?kdk?kdk
2?2?
?????
3s?d?2
2?v?
3
3s
(E?
2?v?2
?
?m
?2d?
e
?/kBT
3s?kBT??E0??12?v?22
?E
)s?T2 ?T
?
?D
D
??????
3??d??
3skTkTkT??BBB?
?/kBTe?12?v?22
2
?
xD
D
x2dx
ex?1
T?0时,E?T3,?Cv?(
3、证明在倒易空间中当k落于一倒格矢Kh的垂直平分面上时,发生布拉格反射。 证明:如图所示当k落于一倒格矢,
的垂直平分面上时,
Kh2??ksin??sin?, 2?
又d=
2?2?
,得布拉格反射公式:2dsin??n?。 =
?KhnKh
4、证明在晶体中不存在5次旋转轴。 证明:对于AB
如果绕A转θ将B转到B’或者绕B将A转到A’点。
转动θ角是晶体的一个对称操作,所以A’和B’也是晶体中的结点。 所以有B'A'?n BA(n取整数)
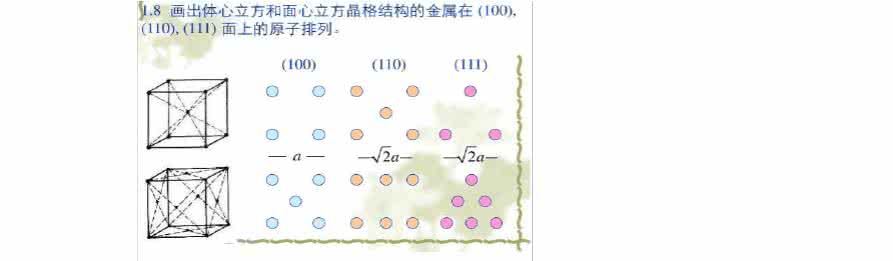
由几何关系B'A'?AB?2ABcos(???)?AB(1?2cos?) 由此可见 n=1-2cos?
由于?1?cos??1,所以n只能取-1,0,1,2,3
2?2?2?2?
对应的θ分别为0(2?),6,4,3,2。
三、计算题
1、求边长为a二维正方晶格的倒点阵,并画出其第一、第二布里渊区。
?a1?ai?
解:二维正方点阵基矢 ?a2?aj
?
?a3?k
2?(a2?a3)2??b??i?1
?a
?
2??
j其倒点阵基矢为?b2?, a?
?b3?k??2?
的正方点阵。 a
其布里渊区如图所示,红色为第一布里渊区, 绿色为第二布里渊区。
倒点阵为边长
2、 对于H2,从气体的测量得到Lennard—Jones参数为??50?10?6J,??2.96A.计算fcc结构的H2的结合能[以KJ/mol单位),每个氢分子可当做球形来处理.结合能的实验值为0.751kJ/mo1,试与计算值比较.
解:以H2为基团,组成fcc结构的晶体,如略去动能,分子间按Lennard—Jones势相互作用,则晶体的总相互作用能为:
6
???12???12??6????U?2N???Pij????Pij???.
?R??R??j??i?
?
j
?P?6?14.45392;
??Pij?12?12.13188,??50?10?16erg,??2.96A,N?6.022?1023/mol. ij
i
将R0代入U得到平衡时的晶体总能量为U?2?6。022?10/mol?50?10
28
?16
126
??2.96??2.96??erg???12.13?????14.45??????2.55KJ/mol.
3.163.16????????
3、 设三维晶格的光学振动在q=0附近的长波极限有?(q)??0?Aq2,求解其态密度。 解:依据?q?(q)??2Aq,f(?)?并带入上边结果有
3
?2???
V
ds
,
?q?(q)
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网