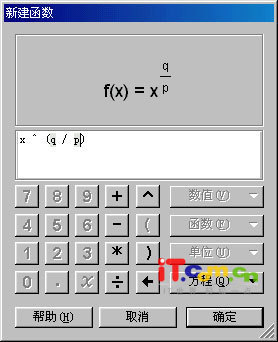
一、主要知识点回顾
1. 四边形有关知识
⑴ n边形的内角和为 .外角和为 .
⑵ 如果一个多边形的边数增加一条,那么这个多边形的内角和增加 ,
外角和增加 .
⑶ n边形过每一个顶点的对角线有 条,n边形的对角线有 条.
2. 平面图形的镶嵌
⑴ 当围绕一点拼在一起的几个多边形的内角加在一起恰好组成一个____________时,就拼成一个平面图形.
⑵ 只用一种正多边形铺满地面,请你写出这样的一种正多边形____________.
3.平行四边形的性质
(1)平行四边形对边______,对角______;角平分线______;邻角______.
(2)平行四边形两个邻角的平分线互相______,两个对角的平分线互相______.(填“平行”或“垂直”)
(3)平行四边形的面积公式____________________.
4.平行四边形的判定
(1)定义法:________________________.
(2)边:________________________或_______________________.
(3)角:________________________.
(4)对角线:________________________.
5. 特殊的平行四边形的之间的关系
6. 特殊的平行四边形的判别条件
要使ABCD成为矩形,需增加的条件是_______ _____ ;
要使ABCD成为菱形,需增加的条件是_______ _____ ;
要使矩形ABCD成为正方形,需增加的条件是______ ____ ;
要使菱形ABCD成为正方形,需增加的条件是______ ____ .
7. 特殊的平行四边形的性质
边
角
对角线
矩形
菱形
正方形
8.梯形
(1).梯形的面积公式是________________.
(2).等腰梯形的性质:边 __________________________________.
角 __________________________________.
对角线 __________________________________.
(3) 等腰梯形的判别方法__________________________________.
(4) 梯形的中位线长等于__________________________.
二、例题精讲
例1. 如图,在等腰梯形ABCD中,AD∥BC.求证:∠A+∠C=180°
变式练习1.已知,如图,□ABCD中,,∠BAD的平分线交BC边于点E.
求证:BE=CD.
例2. 已知:如图,在□ABCD中,BE、CE分别平分 ∠ABC、∠BCD,点E在AD上,BE=12 cm,CE=5 cm.求□ABCD的周长和面积.
变式练习2:如图,在梯形ABCD中,AB∥DC,CB=DC,AD⊥DB于点D,且∠A=60°,DC=2cm.(1)求梯形ABCD的腰长;(2)求梯形ABCD的面积.
例3. 已知:如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F。
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形ABCD是矩形?并证明你结论;
(3)若AC边上存在点O,使四边形AECF是正方形,猜想△ABC的形状并证明你结论.
变式练习3:(2010?青海)观察探究,完成证明和填空.
如图1,四边形ABCD中,点E、F、G、H分别为边AB、BC、CD、DA的中点,顺次连接E、F、G、H,得到四边形EFGH叫中点四边形.
(1)求证:四边形EFGH是平行四边形;
(2)如图2,当四边形ABCD变成等腰梯形时,它的中点四边形是菱形,请你探究并填空:
当四边形ABCD变成平行四边形时,它的中点四边形是 ;
当四边形ABCD变成矩形时,它的中点四边形是 ;
当四边形ABCD变成菱形时,它的中点四边形是 ;
当四边形ABCD变成正方形时,它的中点四边形是 ;
(3)根据以上观察探究,请你总结形状由原什么决定?
(图1)(图2)
变式练习4:. 如图所示,已知AD是△ABC的角平分线,DE∥AC交AB于点E,DF∥AB交AC于点F,
求证:AD⊥EF.
三、巩固与提高
1. 若一个多边形的内角和是外角和的5倍,则这个多边形的边数是 。
2.ABCD中,∠B=30°,AB=4 cm,BC=8 cm,则四边形ABCD的面积是_____.
3. 如图,等腰梯形ABCD的周长为18,腰AD=4,则等腰梯形ABCD的中位线EF= .
(第3题) (第4题)
4.如图,把矩形沿对折后使两部分重合,若,则=( )
A.110° B.115° C.120° D.130°
5.如图,菱形ABCD中,BE⊥AD,BF⊥CD,E、F为垂足,AE=ED,
求∠EBF的度数.
6. 已知:如图,在?ABCD中,点E在AD上,连接BE,DF∥BE交BC于点F,AF与BE交于点M,CE与DF交于点N.
求证:四边形MFNE是平行四边形.
7. 如图,在正方形ABCD中,E、F分别是边BC,CD上的点,∠EAF=45°,AH⊥EF.
(1)求证:AH=AB;
(2)猜想与BE、DF的关系并给出证明.
四、自我检测
1.若n边形每个内角都等于150°,那么这个n边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
2.四边形ABCD中,若∠A︰∠B︰∠C︰∠D=2︰2︰1︰3,那么这个四边形
是( )
A.梯形 B.等腰梯形 C.直角梯形 D.任意四边形
3. 如图,梯形ABCD中,AD∥BC,EF是梯形的中位线,对角线AC交EF于G,若BC=10cm,EF=8cm,则GF的长等于 cm.
4.如图所示,在?ABCD中,对角线AC,BD相交于点O,E,F是对角线AC上的两点,当E,F满足下列哪个条件时,四边形DEBF不一定是平行四边形( )
A、OE=OF B、DE=BF C、∠ADE=∠CBF D、∠ABE=∠CDF
5.如图,△ABC是等边三角形,点P是三角形内的任意一点,PD∥AB,PE∥BC,PF∥AC,若△ABC的周长为12,则PD+PE+PF=( )
A、8 B、6 C、4 D、3
6.如图,AB=CD,BF=ED,AE=CF,由这些条件能得出图中互相平行的线段共有( )
A、1组 B、2组 C、3组 D、4组
(第3题) (第4题) (第5题) (第6题)
7.如图所示,BD,BE分别是∠ABC与它的邻补角∠ABP的平分线.AE⊥BE,AD⊥BC,E,D为垂足,求证:四边形AEBD是矩形.
 爱华网
爱华网