解析几何 三角形面积 例析平面直角坐标系中三角形面积的求法

我们常常会遇到在平面直角坐标系中求三角形面积的问题.解题时我们要注意其中的解题方法和解题技巧.现举例说明如下.

一、有一边在坐标轴上

例1　如图1，平面直角坐标系中，△ABC的顶点坐标分别为（－3，0），（0，3），（0，－1），你能求出三角形ABC的面积吗？

分析：根据三个顶点的坐标特征可以看出，△ABC的边BC在y轴上，由图形可得BC＝4，点A到BC边的距离就是A点到y轴的距离，也就是A点横坐标的绝对值3，然后根据三角形的面积公式求解.

解：因为B(0,3),C(0,-1),所以BC=3-（-1）=4.因为A(-3,0),所以A点到y轴的距离，即BC边上的高为3，

二、有一边与坐标轴平行

例2　如图2，三角形ABC三个顶点的坐标分别为A（4，1），B（4，5），C（-1，2），求三角形ABC的面积.

分析：由A（4，1），B（4，5）两点的横坐标相同，可知边AB与y轴平行，因而AB的长度易求.作AB边上的高CD，则D点的横坐标与A点的横坐标相同，也是4，这样就可求得线段CD的长，进而可求得三角形ABC的面积.

解：因为A，B两点的横坐标相同，所以边AB∥y轴，所以AB=5-1=4. 作AB边上的高CD，则D点的横坐标为4，所以CD=4-（-1）=5，所以=.

三、三边均不与坐标轴平行

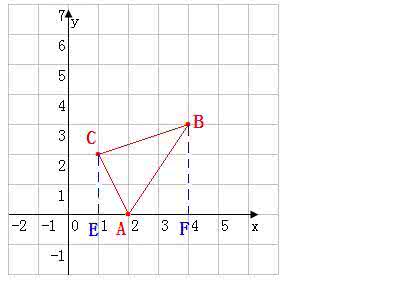
例3　如图2,平面直角坐标系中，已知点A（-3，-1），B（1，3），C（2，-3），你能求出三角形ABC的面积吗？

分析：由于三边均不平行于坐标轴，所以我们无法直接求边长，也无法求高，因此得另想办法.根据平面直角坐标系的特点，可以将三角形围在一个梯形或长方形中，这个梯形（长方形）的上下底（长）与其中一坐标轴平行，高（宽）与另一坐标轴平行.这样，梯形（长方形）的面积容易求出，再减去围在梯形（长方形）内边缘部分的直角三角形的面积，即可求得原三角形的面积.

解：如图，过点A、C分别作平行于y轴的直线，与过点B平行于x轴的直线交于点D、E，则四边形ADEC为梯形.因为A（-3，-1），B（1，3），C（2，-3），所以AD＝4，CE=6，DB=4，BE=1，DE＝5.所以=（AD+CE）×DE-AD×DB-CE×BE=×（4+6）×5－×4×4－×6×1＝14.

爱华网本文地址 » http://www.aihuau.com/a/399951/611965722500.html