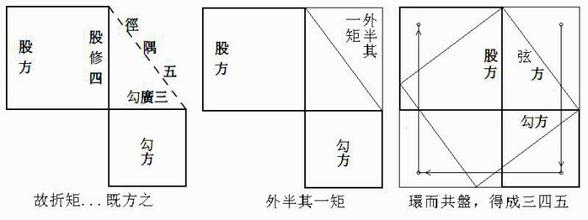
几何:勾股定理及逆定理的综合应用。
二. 重点、难点
重点:
代数:。
几何:勾股定理,逆定理的应用。
难点:
代数:计算准确度及二次根式乘法条件。
几何:勾股定理、逆定理的应用。
学习目标:
代数:掌握简单的二次根式的乘法与化简,二次根式的比较大小以及联系勾股定理解决实际问题。
几何:进一步理解勾股定理与逆定理之间的关系。
三. 知识要点:
代数
几何:
【典型例题】
例1. 化简
(1) (2)
(3)
(4)
分析:(1),任何一个非负数都可以写成一个非负数的平方。
(2),积的算术平方根的性质。
(3)平方差公式。
(4)整数指数幂的运算性质。
解:(1)
(2)
(3)
(4)
例2. 化简
(1) (2) (3)
分析:(1)(2)利用的变形
(3)被开方数是小数乘积,可先写成整数与小数乘积。
解:(1)
(2)
(3)
注意:不能写成,必须写成
例3. 判断下列变形是否正确
(1)( )
(2)( )
(3)( )
(4)a、b异号,则( )
解:(1)×
(2)×
∵a不知正负,不能随便移进根号下。
(3)√
的符号一定为正或
(4)×
例4. 如图所示,在四边形ABCD中,,若AB=2,CD=1,求四边形ABCD的面积。
分析:不规则四边形求面积,可利用分割法来求。
解:过B作,在Rt△ABE中,
又四边形CDEF为矩形
在Rt△BCF中,
例5. 在△ABC中,AB=AC,P为BC上任意一点,求证:。
分析:构造直角三角形,才可能出现边的平方的关系。
证明:(1)如果,
在Rt△ABP中,
故结论得证
(2)如果AP不垂直于BC,作BC边的高AD。
在Rt△APD中,
在Rt△ACD中,
【模拟试题】(答题时间:30分钟)
1. 化简
(1)
(2)
(3)
(4)
(5)
2. 比较下列两数的大小(不查表)
(1);
(2);
3. 如图所示,在四边形ABCD中,AB=4,BC=13,CD=12,AD=3,,求四边形ABCD的面积。
4. 已知两条线段的长分别为9cm和41cm时,求当第三条线段多长时,这三条线段可组成一个直角三角形。
【试题答案】
1. 化简
(1) (2)
(3) (4)
(5)
2. (1)> (2)<
3. ,利用割补法
4. 第三条线段为40或
 爱华网
爱华网