作者:王方汉,ID为大罕,男,湖北省武汉市人。中学数学高级教师。全国初等数学研究会常务理事,广东省初等数学学会顾问。曾任《数学通讯》编委,《中学数学》编委。在国家级和省级刊物上发表数学论文三百余篇,曾获全国初等数学研究大会论文一等奖。编著数学书数本,代表著作为《五角星·星形·平面闭折线》(华中师范大学出版社)此篇咏“五心”,2014.6.29.写于沪上
重心
中线交汇乃重心
四平八稳踏歌行
三分天下无异界
一二比例探路明解读中线交汇乃重心注:三角形三条中线交于一点,此点称为重心。在解决数学问题时,可以理解为经过顶点与重心的直线平分对边
四平八稳踏歌行注:重心是三角形的稳定点
三分天下无异界注:重心与三顶点的连线三等分三角形面积(图中△GAB、△GAC、△GBC面积相同)
一二比例探路明注:重心到对边中点距离是到顶点距离的2倍.垂心
作高必垂生此心,
几番梦成相似形。
四点共圆天伦享,
欧拉一线百媚生。解读作高必垂生此心,注:三角形三条高线交于一点,此点称为垂心
几番梦成相似形。
注:图形中有若干对相似三角形
四点共圆天伦享,
注:垂心、垂足、顶点中有若干组四点共圆
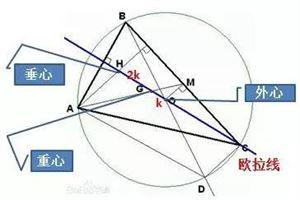
欧拉一线百媚生。注:外心、重心、垂心三点共线,称为欧拉线,且外心到重心距离与重心到垂心距离之比为1比2(下图详细介绍欧拉线)
内心
三角平分线相交,
一圆内切见窈窕。
君念周边等距离,
边偕半径藏奥妙。解读三角平分线相交注:三角形三个内角的平分线交于一点,此点称为内心
一圆内切见窈窕注:以内心为圆心可作一个内切圆。
君念周边等距离注:内心到三角形的三边距离相等。
边偕半径藏奥妙注:内切圆半径长可用三角形的三边来表示。普通三角形内接圆半径:r=2S/(a+b+c)直角三角形内切圆半径:r=(a+b-c)/2【c是斜边】外心
三角形嵌外接圆,
边唱角随拨正弦。
三厢有礼前路远,
棱角有致世间传。
解读三角形嵌外接圆注:三角形三条边的垂直平分线交于一点,此点称为外心。
边唱角随拨正弦注:正弦定理:三角形一边与对角正弦之比是外接圆直径长。(a/SinA=b/SinB=c/SinC=2R)
三厢有礼前路远注:外心到三角形三顶点等距离,此距离为外接圆的半径长度。旁心珠圆旁置心也甘,延线吻切情依然。
张角舒展凌云志,诸心合璧现奇观。解读珠圆旁置心也甘,注:三角形一角平分线及另两角外角平分线交于一点,此点称为旁心
延线吻切情依然。
注:旁切圆的切点在一边和另两边的延长线上
张角舒展凌云志,注:关于旁心有张角定理(如下图1)
诸心合璧现奇观。注:连接三旁心的三角形过原三角形三顶点,旁心与内心连线的中点在三角形外接圆上(如下图2)
 爱华网
爱华网