17.想 法 则
用来说明运算规律(或方法)的文字,叫做法则。
子比分母少16。求这个分数?
由“一个分数乘以5,是分子乘以5分母不变”,结果是分子的5倍比3倍比分母少16。知
分子的5-3=2(倍)是2+16=18,分子为18÷2=9,分母为9×5-2=43或9×3+16=43。
18.想 公 式
证明方法:
以分母a,要加(或减)的数为
(2)设分子加上(或减去)的数为x,分母应加上(或减去)的数为y。
19.想 性 质
例1 1992年小学数学奥林匹克试题初赛(C)卷题6:有甲、乙两个多少倍?
200÷16=12.5(倍)。
例2 思考题:三个最简真分数,它们的分子是连续自然数,分母大于10,且它们最小公分母是60;其中一个分数的值,等于另两个分数的和。写出这三个分数。
由“分母都大于10,且最小公分母是60”,知其分母只能是12、15、20;12、15、30;12、15、60。
由“分子是连续自然数”,知分子只能是小于12的自然数。
满足题意的三个分数是
(二)第400个分数是几分之几?
此题特点:
(2)每组分子的排列:
假设某一组分数的分母是自然数n,则分子从1递增到n,再递减到1。分数的个数为n+n-1=2n-1,即任何一组分数的个数总是奇数。
(3)分母数与分数个数的对应关系,正是自然数与奇数的对应关系
分母:1、2、3、4、5、……
分数个数:1、3、5、7、9、……
(4)每组分数之前(包括这组本身)所有分数个数的和,等于这组的组号(这一组的分母)的平方。
例如,第3组分数前(包括第3组)所有分数个数的和是32=9。
10×2-1-6=13(个)位置上。
分别排在81+7=88(个),81+13=94(个)的位置上。
或者102=100, 100-12=88。
100-6=94, 88+6=94。
问题(二):由上述一串分数个数的和与组号的关系,将400分成某数的平方,这个数就是第400个分数所在的组数400=202,分母也是它。
第400个分数在第20组分数中,400是这20组分数的和且正好是20的平方无剩余,故可断定是最后一个,即
若分解为某数的平方有剩余,例如,第415个和385个分数各是多少。
逆向思考,上述的一串分数中,分母是35的排在第几到第几个?
352-(35×2-1)+1
=1225-69+1=1157。
排在1157-1225个的位置上。
20.由规则想
例如,1989年从小爱数学邀请赛试题:接着1989后面写一串数字,写下的每一个数字都是它前面两个数字的乘积的个位数字。
例如,8×9=72,在9后面写2,9×2=18,在2后面写8,……得到一串数:1989286……
这串数字从1开始往右数,第1989个数字是什么?
先按规则多计算几个数字,得1989286884286884……显然,1989后面的数总是不断重复出现286884,每6个一组。
(1989-4)÷6=330……5
最后一组数接着的五个数字是28688,即第1989个数字是8。
21.用 规 律
例1 第六册P62第14题:选择“+、-、×、÷”中的符号,把下面各题连成算式,使它们的得数分别等于0、1、2、3、4、5、6、7、8、9。
(1)2 2 2 2 2=0
(2)2 2 2 2 2=1
……
(10)2 2 2 2 2=9
解这类题的规律是:
先想用两、三个2列出,结果为0、1、2的基本算式:
2-2=0,2÷2=1;
再联想2-2÷2=1,2×2÷2=2,2÷2+2=3,……
每题都有几种选填方法,这里各介绍一种:
2÷2+2÷2-2=0
2÷2×2-2÷2=1
2-2+2÷2×2=2
2×2+2÷2-2=3
2×2×2-2-2=4
2-2÷2+2×2=5
2+2-2+2×2=6
2×2×2-2÷2=7
2÷2×2×2×2=8
2÷2+2×2×2=9
例2 第六册P63题4:写出奇妙的得数
2+1×9=
3+12×9=
4+123×9=
5+1234×9=
6+12345×9=
得数依次为11、111、1111、11111、111111。此组算式的特点:
第一个加数由2开始,每式依次增加1。第二个加数由乘式组成,被乘数的位数依次为1、12、123、……继续写下去
7+123456×9=1111111
8+1234567×9=11111111
9+12345678×9=111111111
10+123456789×9=1111111111
11+1234567900×9=11111111111
12+12345679011×9=111111111111
……
很自然地想到,可推广为
(1)当n=1、2时,等式显然成立。
(2)设n=k时,上式正确。当n=k+1时
k+1+123…k×9
=k+1+[123…(k-1)×10+k]×9
=k+1+123…(k-1)×9×10+9k
=[k+123…(k-1)×9]×10+1
根据数学归纳法原理,由(1)、(2)可断定对于任意的自然数n,此等式都成立。
例3 牢记下面两个规律,可随口说出任意一个自然数作分母的,所有真分数的和。
(1)奇数(除1外)作分母的所有真分数的和、是(分母-1)÷2。
=(21-1)÷2=10。
22.巧想条件
比5小,分母是13的最简分数有多少个。
7~64为64-(7-1)=58(个),去掉13的倍数13、26、39、52,余下的作分子得54个最简分数。
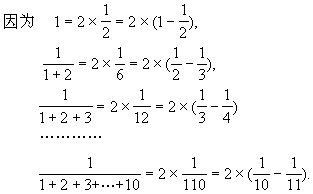
例2 一个整数与1、2、3,通过加减乘除(可添加括号)组成算式,若结果为24这个整数就是可用的。4、5、6、7、8、9、10中,有几个是可用的。
看结果,想条件,知都是可用的。
4×(1+2+3)=24
(5+1+2)×3=24
6×(3+2-1)=24
7×3+1+2=24
8×3÷(2-1)=24
9×3-1-2=24
10×2+1+3=24
 爱华网
爱华网