各地中考数学压轴题 2012年各地中考数学压轴题

<?xml:namespace prefix = o ns = "urn:schemas-microsoft-com:office:office" />

 2012年各地中考数学压轴题

23．（12分）如图1，在直角坐标系中，已知点A（0，2）、点B（-2，0），过点B和线段OA的中点C作直线BC，以线段BC为边向上作正方形BCDE.

（1）填空：点D的坐标（      ），点E的坐标为（      ）.

（2）若抛物线<?xml:namespace prefix = v ns = "urn:schemas-microsoft-com:vml" />经过A、D、E三点，求该抛物线的解析式.

（3）若正方形和抛物线均以每秒个单位长度的速度沿射线BC同时向上平移，直至正方形的顶点E落在轴上时，正方形和抛物线均停止运动.

①在运动过程中，设正方形落在y轴右侧部分的面积为，求关于平移时间（秒）的函数关系式，并写出相应自变量的取值范围.

<?xml:namespace prefix = w ns = "urn:schemas-microsoft-com:office:word" />②运动停止时，求抛物线的顶点坐标.

24．（本题满分11分）已知抛物线 经过

A（2，0）． 设顶点为点P，与x轴的另一交点为点B．

（1）求b的值，求出点P、点B的坐标；

（2）如图，在直线 y= x上是否存在点D，使四边形OPBD为平行四边形？若存在，求出点D的坐标；若不存在，请说明理由；

A

P

B

x

y

O

（第24题图）

25.（本小题满分10分）已知抛物线的函数解析式为，若抛物线经过点，方程的两根为，，且。

（1）求抛物线的顶点坐标.

（2）已知实数，请证明：≥,并说明为何值时才会有.

（3）若抛物线先向上平移4个单位，再向左平移1个单位后得到抛物线，设，是 上的两个不同点，且满足：，，.请你用含有的表达式表示出△的面积，并求出的最小值及取最小值时一次函数的函数解析式。

（参考公式：在平面直角坐标系中，若，，则，两点间的距离为 ）

24．（12分）如图，在矩形ABCD中，AB＝12cm，BC＝8cm，点E，F，G分别从点A，B，C三点同时出发，沿矩形的边按逆时针方向移动，点E，G的速度均为2cm/s，点F的速度为4cm/s，当点F追上点G（即点F与点G重合）时，三个点随之停止移动．设移动开始后第t秒时，△EFG的面积为S（cm2）．

（1）当t＝1秒时，S的值是多少？

（2）写出S和t之间的函数解析式，并指出自变量t的取值范围．

（第24题图）

5

2

3

1

O

y

x

Q

P

2

P

1

图1

若 ，则点 与点 的非常距离为 ；

若 ，则点 与点 的非常距离为 ；

例如：点 （1，2），点 （3，5），因为 ，所以点 与点 的“非常距离”为 ，也就是图1中线段 与线段 长度的较大值（点Q为垂直于y轴的直线 与垂直于x轴的直线 的交点）．

（1）已知点A（ ，0），B为y轴上的一个动点，

①若点A与点B的“非常距离”为2，写出一个满足条件的点B的坐标；

②直接写出点A与点B的“非常距离”的最小值．

（2）已知C是直线 上的一个动点，

①如图2，点D的坐标是（0，1），求点C与点D的“非常距离”的最小值及相应的点C的坐标；

②如图3，E是以原点O为圆心，1为半径的圆上的一个动点，求点C与点E的“非常距离”的最小值及相应点E和点C的坐标．

x

1

O

y

D

x

1

O

y

图2                                         图3

26．如图半径分别为m，n（0＜m＜n）的两圆⊙O1和⊙O2相交于P，Q两点，且点P（4，1），两圆同时与两坐标轴相切，⊙O1与x轴，y轴分别切于点M，点N，⊙O2与x轴，y轴分别切于点R，点H．

（1）求两圆的圆心O1，O2所在直线的解析式；

（2）求两圆的圆心O1，O2之间的距离d；

（3）令四边形PO1QO2的面积为S1，四边形RMO1O2的面积为S2．

试探究：是否存在一条经过P，Q两点、开口向下，且在x轴上截得的线段长为 的抛物线？若存在，请求出此抛物线的解析式；若不存在，请说明理由．

25、(本小题12分).如同，抛物线 与 轴交于C、A两点，与y轴交于点B，OB=4点O关于直线AB的对称点为D，E为线段AB的中点.

（1） 分别求出点A、点B的坐标

y

x

B

D

P

A

Q

O

C

2

（3） 若反比例函数 的图像过点D，求 值.

（4）两动点P、Q同时从点A出发，分别沿AB、

AO方向向B、O移动，点P每秒移动1个单位，点Q

每秒移动 个单位，设△POQ的面积为S，移动时间

为t,问：S是否存在最大值？若存在，求出这个最大值，

并求出此时的t值，若不存在，请说明理由.

26.如图，在Rt△ABC中,∠ACB=90°，AC=8cm,BC=4cm,D、E分别为边AB、BC的中点，连结DE.点P从点A出发，沿折线AD-DE-EB运动,到点B停止．点P在AD上以 cm/s的速度运动，在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时，过点P作PQ⊥AC于点Q，以PQ为边作正方形PQMN，使点M落在线段AC上.设点P的运动时间为t（s）.

（1）当点P在线段DE上运动时，线段DP的长为     cm（用含t的代数式表示）.

（2）当点N落在AB边上时，求t的值.

（3）当正方形PQMN与△ABC重叠部分图形为五边形时，设五边形的面积为S(cm2)，求S与t的函数关系式.

（4）连结CD.当点N与点D重合时，有一点H从点M出发，在线段MN上以2.5cm/s的速度沿M-N-M连续做往返运动，直至点P与点E重合时，点H停止往返运动；当点P在线段EB上运动时，点H始终在线段MN的中点处. 直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.

26．如图，在平面直角坐标系xOy中，AB⊥x轴于点B，AB=3，tan∠AOB= ，将△OAB绕着原点O逆时针旋转90°，得到△OA1B1；再将△OA1B1绕着线段OB1的中点旋转180°，得到△OA2B1，抛物线y=ax2+bx+c（a≠0）经过点B、B1、A2．

（1）求抛物线的解析式．

（2）在第三象限内，抛物线上的点P在什么位置时，△PBB1的面积最大？求出这时点P的坐标．

（3）在第三象限内，抛物线上是否存在点Q，使点Q到线段BB1的距离为 ？若存在，求出点Q的坐标；若不存在，请说明理由．

22．如图，抛物线y= x2﹣ x﹣9与x轴交于A、B两点，与y轴交于点C，连接BC、AC．

（1）求AB和OC的长；

（2）点E从点A出发，沿x轴向点B运动（点E与点A、B不重合），过点E作直线l平行BC，交AC于点D．设AE的长为m，△ADE的面积为s，求s关于m的函数关系式，并写出自变量m的取值范围；

（3）在（2）的条件下，连接CE，求△CDE面积的最大值；此时，求出以点E为圆心，与BC相切的圆的面积（结果保留π）．

26．(12分)如图，在△ABC中，∠BAC＝90°，AB＝AC＝6，D为BC的中点．

(1)若E、F分别是AB、AC上的点，且AE＝CF，求证：△AED≌△CFD；

(2)当点F、E分别从C、A两点同时出发，以每秒1个单位长度的速度沿CA、AB运动，到点A、B时停止；设△DEF的面积为y，F点运动的时间为x，求y与x的函数关系式；

(3)在(2)的条件下，点F、E分别沿CA、AB的延长线继续运动，求此时y与x的函数关系式．

26．如图所示，在平面直角坐标系xOy中，矩形OABC的边长OA、OC分别为12cm、6cm，点A、C分别在y轴的负半轴和x轴的正半轴上，抛物线y=ax2+bx+c经过点A、B，且18a+c=0．

（1）求抛物线的解析式．

（2）如果点P由点A开始沿AB边以1cm/s的速度向终点B移动，同时点Q由点B开始沿BC边以2cm/s的速度向终点C移动．

①移动开始后第t秒时，设△PBQ的面积为S，试写出S与t之间的函数关系式，并写出t的取值范围．

②当S取得最大值时，在抛物线上是否存在点R，使得以P、B、Q、R为顶点的四边形是平行四边形？如果存在，求出R点的坐标；如果不存在，请说明理由．

24. 如图甲，四边形OABC的边OA、OC分别在x轴、y轴的正半轴上，顶点在B点的抛物线交x轴于点A、D，交y轴于点E，连接AB、AE、BE．已知tan∠CBE= ，A（3，0），D（﹣1，0），E（0，3）．

（1）求抛物线的解析式及顶点B的坐标；

（2）求证：CB是△ABE外接圆的切线；

（3）试探究坐标轴上是否存在一点P，使以D、E、P为顶点的三角形与△ABE相似，若存在，直接写出点P的坐标；若不存在，请说明理由；

（4）设△AOE沿x轴正方向平移t个单位长度（0＜t≤3）时，△AOE与△ABE重叠部分的面积为s，求s与t之间的函数关系式，并指出t的取值范围．

25．如图1，点A为抛物线C1：y= x2﹣2的顶点，点B的坐标为（1，0）直线AB交抛物线C1于另一点C

（1）求点C的坐标；

（2）如图1，平行于y轴的直线x=3交直线AB于点D，交抛物线C1于点E，平行于y轴的直线x=a交直线AB于F，交抛物线C1于G，若FG：DE=4：3，求a的值；

（3）如图2，将抛物线C1向下平移m（m＞0）个单位得到抛物线C2，且抛物线C2的顶点为点P，交x轴于点M，交射线BC于点N．NQ⊥x轴于点Q，当NP平分∠MNQ时，求m的值．

25．如图，在△ABC中，AB=AC，∠B=30°，BC=8，D在边BC上，E在线段DC上，DE=4，△DEF是等边三角形，边DF交边AB于点M，边EF交边AC于点N．

（1）求证：△BMD∽△CNE；

（2）当BD为何值时，以M为圆心，以MF为半径的圆与BC相切？

（3）设BD=x，五边形ANEDM的面积为y，求y与x之间的函数解析式（要求写出自变量x的取值范围）；当x为何值时，y有最大值？并求y的最大值．

28. （本题满分12分）

如图，在平面直角坐标系xoy中，已知直线l1:y=x与直线l2：y=-x+6相交于点M，直 线l2与x轴 相较于点N.

（1）    求M，N的坐标；

（2）    在矩形ABCD中，已知AB=1，BC=2，边AB在x轴上，矩形ABCD沿x轴自左向右以每秒1个单位长度的速度移动.设矩形ABCD与△OMN的重叠部分的面积为S.移动的时间为t（从点B与点O重合时开始计时，到点A与点N重合时计时结束）。直接写出S与自变量t之间的函数关系式（不需要给出解答过程）；

（3）    在（2）的条件下，当t为何值时，S的值最大？并求出最大值.

A

B

C

D

N

M

x

y

l1

l2

O

29.（10分）如图，已知抛物线 与x轴的正半轴分别交于点A、B（点A位于点B的左侧），与y轴的正半轴交于点C.

    ⑴点B的坐标为  ▲  ，点C的坐标为  ▲  （用含b的代数式表示）；

⑵请你探索在第一象限内是否存在点P，使得四边形PCOB的面积等于2b，且△PBC是以点P为直角顶点的等腰直角三角形？如果存在，求出点P的坐标；如果不存在，请说明理由；

⑶请你进一步探索在第一象限内是否存在点Q，使得△QCO、△QOA和△QAB中的任意两个三角形均相似（全等可看作相似的特殊情况）？如果存在，求出点Q的坐标；如果不存在，请说明理由.

24.已知,纸片⊙O的半径为2,如图1,沿弦AB折叠操作.

   (1)如图2,当折叠后的AB经过圆心O时,求AB弧的长;

   (2)如图3,当弦AB=2时,求折叠后AB弧所在圆的圆心O′到弦AB的距离;

   (3)在图1中,再将纸片⊙O沿弦CD折叠操作.

     ①如图4,当AB∥CD,折叠后的CD弧与AB弧所在圆外切于点P,设点O到弦AB、CD的距离之和为 ，求 的值；

     ②如图5，当AB与CD不平行，折叠后的CD弧与AB弧所在圆外切于点P时,设点M为AB的中点，点N为CD的中点.试探究四边形OMPN的形状,并证明你的结论.

23．如图，矩形OABC中，A（6，0）、C（0，2 ）、D（0，3 ），射线l过点D且与x轴平行，点P、Q分别是l和x轴正半轴上动点，满足∠PQO=60°．

（1）①点B的坐标是　　；②∠CAO=　　度；③当点Q与点A重合时，点P的坐标为　　；（直接写出答案）

（2）设OA的中心为N，PQ与线段AC相交于点M，是否存在点P，使△AMN为等腰三角形？若存在，请直接写出点P的横坐标为m；若不存在，请说明理由．

（3）设点P的横坐标为x，△OPQ与矩形OABC的重叠部分的面积为S，试求S与x的函数关系式和相应的自变量x的取值范围．

23．如图所示，现有一张边长为4的正方形纸片ABCD，点P为正方形AD边上的一点（不与点A、点D重合）将正方形纸片折叠，使点B落在P处，点C落在G处，PG交DC于H，折痕为EF，连接BP、BH．

（1）求证：∠APB=∠BPH；

（2）当点P在边AD上移动时，△PDH的周长是否发生变化？并证明你的结论；

（3）设AP为x，四边形EFGP的面积为S，求出S与x的函数关系式，试问S是否存在最小值？若存在，求出这个最小值；若不存在，请说明理由．

25.如图，在半径为2的扇形AOB中，∠AOB=90°，点C是弧AB上的一个动点（不与点A、B重合）OD⊥BC，OE⊥AC，垂足分别为D、E．

（1）当BC=1时，求线段OD的长；

（2）在△DOE中是否存在长度保持不变的边？如果存在，请指出并求其长度，如果不存在，请说明理由；

（3）设BD=x，△DOE的面积为y，求y关于x的函数关系式，并写出它的定义域．

26．如图，在平面直角坐标系中，点A的坐标为（m，m），点B的坐标为（n，﹣n），抛物线经过A、O、B三点，连接OA、OB、AB，线段AB交y轴于点C．已知实数m、n（m＜n）分别是方程x2﹣2x﹣3=0的两根．

（1）求抛物线的解析式；

（2）若点P为线段OB上的一个动点（不与点O、B重合），直线PC与抛物线交于D、E两点（点D在y轴右侧），连接OD、BD．

①当△OPC为等腰三角形时，求点P的坐标；

②求△BOD 面积的最大值，并写出此时点D的坐标．

25．抛物线 的顶点在直线y=x+3上，过点F（﹣2，2）的直线交该抛物线于点M、N两点（点M在点N的左边），MA⊥x轴于点A，NB⊥x轴于点B．

（1）先通过配方求抛物线的顶点坐标（坐标可用含m的代数式表示），再求m的值；

（2）设点N的横坐标为a，试用含a的代数式表示点N的纵坐标，并说明NF=NB；

（3）若射线NM交x轴于点P，且PA?PB= ，求点M的坐标．

29．如图，半径为2的⊙C与x轴的正半轴交于点A，与y轴的正半轴交于点B，点C的坐标为（1，0）．若抛物线 过A、B两点．

（1）求抛物线的解析式；

（2）在抛物线上是否存在点P，使得∠PBO=∠POB？若存在，求出点P的坐标；若不存在说明理由；

（3）若点M是抛物线（在第一象限内的部分）上一点，△MAB的面积为S，求S的最大（小）值．

25．(满分14分)如图，在□ OABC中，点A在x轴上，∠AOC=60o，0C=4cm．OA=8cm．动点P从点0出发，以1cm／s的速度沿线段OA→AB运动；动点Q同时从点O出发，以

    acm／s的速度沿线段OC→CB运动，其中一点先到达终点B时，另一点也随之停止运动．

    设运动时间为t秒．

    (1)填空：点C的坐标是(______，______)，对角线OB的长度是_______cm；

(2)当a=1时，设△OPQ的面积为S，求S与t的函数关系式，并直接写出当t为何值

       时，S的值最大?   

    (3)当点P在OA边上，点Q在CB边上时，线段PQ与对角线OB交于点M.若以O、M、P

      为顶点的三角形与△OAB相似，求a与t的函数关系式，并直接写出t的取值范围．

24．如图，把两个全等的Rt△AOB和Rt△COD分别置于平面直角坐标系中，使直角边OB、OD在x轴上．已知点A（1，2），过A、C两点的直线分别交x轴、y轴于点E、F．抛物线y=ax2+bx+c经过O、A、C三点．

（1）求该抛物线的函数解析式；

（2）点P为线段OC上一个动点，过点P作y轴的平行线交抛物线于点M，交x轴于点N，问是否存在这样的点P，使得四边形ABPM为等腰梯形？若存在，求出此时点P的坐标；若不存在，请说明理由．

（3）若△AOB沿AC方向平移（点A始终在线段AC上，且不与点C重合），△AOB在平移过程中与△COD重叠部分面积记为S．试探究S是否存在最大值？若存在，求出这个最大值；若不存在，请说明理由．

21. 如图，在等腰梯形ABCD中，ABDC，AB= ，DC= ，高CE= ，对角线AC、BD交于H，平行于线段BD的两条直线MN、RQ同时从点A出发沿AC方向向点C匀速平移，分别交等腰梯形ABCD的边于M、N和R、Q，分别交对角线AC于F、G；当直线RQ到达点C时，两直线同时停止移动．记等腰梯形ABCD被直线MN扫过的图形面积为S1、被直线RQ扫过的图形面积为S2，若直线MN平移的速度为1单位/秒，直线RQ平移的速度为2单位/秒，设两直线移动的时间为x秒．

（1）填空：∠AHB=　 　；AC=　   ；

（2）若S2=3S1，求x；

（3）设S2=mS1，求m的变化范围．

25，(本小题满分14分)

    如图，在平面直角坐标系中，矩形OABC四个顶点的坐标分别为O(0，0)，A(0，3)，B(6，3)，C(6，0)，抛物线 过点A。

(1)(2分)求c的值；    ．

(2)(6分)若 ＝－l，且抛物线与矩形有且只有三个交点A、D、E，求△ADE的面积S的最大值；

(3)(6分)若抛物线与矩形有且只有三个交点A、M、N，线段MN的垂直平分线 过点0，交线段BC于点F。当BF＝1时，求抛物线的解析式．

24．(本题满分10分)在Rt△ABC中，∠C=90°，AC=3，BC=4，AB=5.

（Ⅰ)探究新知

如图① ⊙O是△ABC的内切圆，与三边分别相切于点E、F、G..

（1）求证内切圆的半径r1=1;

（2）求tan∠OAG的值；

（Ⅱ）结论应用

（1）如图②若半径为r2的两个等圆⊙O1、⊙O2外切，且⊙O1与AC、AB相切，⊙O2与BC、AB相切，求r2的值；

（2）如图③若半径为rn的n个等圆⊙O1、⊙O2、…、⊙On依次外切，且⊙O1与AC、AB相切，⊙On与BC、AB相切，⊙O1、⊙O2、…、⊙On均与AB相切，求rn的值.

26．（本题满分12分）已知点A(1，c)和点B (3，d )是直线y＝k1x＋b与双曲线y＝（k2＞0）的交点．

　  （1）过点A作AM⊥x轴，垂足为M，连结BM．若AM＝BM，求点B的坐标；

    （2）设点P在线段AB上，过点P作PE⊥x轴，垂足为E，并交双曲线y＝（k2＞0）于点N．当 取最大值时，若PN＝ ，求此时双曲线的解析式．

1. 如图12，在平面直角坐标系中，点A，C分别在 轴， 轴上，四边形ABCO为矩形，AB=16，点D与点A关于 轴对称，tan∠ACB= ，点E，F分别是线段AD，AC上的动点（点E不与点A，D重合），且∠CEF=∠ACB。

（1）求AC的长和点D的坐标；

（2）说明△AEF与△DCE相似；

（3）当△EFC为等腰三角形时，求点E的坐标。

26．（14分）已知抛物线：

（1）求抛物线 的顶点坐标.

（2）将抛物 线 向右平移2个单位，再向上平移1个单位，得到抛物线 ，求抛物线 的解析式.

（3）如下图，抛物线 的顶点为P， 轴上有一动点M，在 、 这两条抛物线上是否存在点N，使O（原点）、P、M、N四点构成以OP为一边的平行四边形，若存在，求出N点的坐标；若不存在，请说明理由.

【提示：抛物线（≠0）的对称轴是

顶点坐标是】

28．如图，Rt△ABO的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上，O为坐标原点，A、B两点的坐标分别为(－3，0)、(0，4)，抛物线y＝x2＋bx＋c经过点B，且顶点在直线x＝上．

(1)求抛物线对应的函数关系式；

(2)若把△ABO沿x轴向右平移得到△DCE，点A、B、O的对应点分别是D、C、E，当四边形ABCD是菱形时，试判断点C和点D是否在该抛物线上，并说明理由；

(3)在(2)的条件下，连接BD，已知对称轴上存在一点P使得△PBD的周长最小，求出P点的坐标；

(4)在(2)、(3)的条件下，若点M是线段OB上的一个动点(点M与点O、B不重合)，过点M作∥BD交x轴于点N，连接PM、PN，设OM的长为t，△PMN的面积为S，求S和t的函数关系式，并写出自变量t的取值范围，S是否存在最大值？若存在，求出最大值和此时M点的坐标；若不存在，说明理由．

23.如图，在平面直角坐标系中，直线：y=－2x＋b (b≥0)的位置随b的不同取值而变化．

    (1)已知⊙M的圆心坐标为(4，2)，半径为2．

    当b=　　　　时，直线：y=－2x＋b (b≥0)经过圆心M：

    当b=　　　　时，直线：y=－2x＋b(b≥0)与OM相切：

    (2)若把⊙M换成矩形ABCD，其三个顶点坐标分别为：A(2，0)、B（6，0）、C(6，2).

    设直线扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式，

25．（本小题满分10分）

   已知二次函数 图象的顶点横坐标是2，与 轴交于A（ ，0）、

B（ ，0）， ﹤0﹤ ，与 轴交于点C， 为坐标原点， ．[来源:学科网]

（1）求证： ；

（2）求 、 的值；

（3）当 ﹥0且二次函数图象与直线 仅有一个交点时，求二次函数的最大值．

26．（本题满分12分）如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A（－2，0）、B（0，1）、C（d，2）。

x

B

y

A′

O

C

A

G

B′

C′

（1）求d的值；

（2）将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图像上。请求出这个反比例函数和此时的直线B′C′的解析式；

（3）在（2）的条件下，直线BC交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P，使得四边形PGMC′是平行四边形。如果存在，请求出点M和点P的坐标；如果不存在，请说明理由。

25．如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于E，设∠ABC=α（60°≤α＜90°）．

（1）当α=60°时，求CE的长；

（2）当60°＜α＜90°时，

①是否存在正整数k，使得∠EFD=k∠AEF？若存在，求出k的值；若不存在，请说明理由．

②连接CF，当CE2﹣CF2取最大值时，求tan∠DCF的值．

27. （本题16分）如图，直线1经过点A（-1，0），直线2经过点B(3,0), 1、2均为与轴交于点C(0,),抛物线经过A、B、C三点。

（1）求抛物线的函数表达式；

（2）抛物线的对称轴依次与轴交于点D、与2交于点E、与抛物线交于点F、与1交于点G。求证：DE=EF=FG;[www.#&zzst%e~p.c@om]

(3)若1⊥2于轴上的C点处，点P为抛物线上一动点，要使△PCG为等腰三角形，请写出符合条件的点P的坐标，并简述理由。

25．如图1，已知△ABC中，AB=10cm，AC=8cm，BC=6cm．如果点P由B出发沿BA方向点A匀速运动，同时点Q由A出发沿AC方向向点C匀速运动，它们的速度均为2cm/s．连接PQ，设运动的时间为t（单位：s）（0≤t≤4）．解答下列问题：

（1）当t为何值时，PQ∥BC．

（2）设△AQP面积为S（单位：cm2），当t为何值时，S取得最大值，并求出最大值．

（3）是否存在某时刻t，使线段PQ恰好把△ABC的面积平分？若存在，求出此时t的值；若不存在，请说明理由．

（4）如图2，把△AQP沿AP翻折，得到四边形AQPQ′．那么是否存在某时刻t，使四边形

AQPQ′为菱形？

26．（本小题满分12分）

如图 和图 ，在 中，

探究

在如图 ， 于点 ，则 _______， _______， 的面积 =___________．

拓展

如图 ，点 在 上（可与点 重合），分别过点 作直线 的垂线，垂足为 .设 （当点 与点 重合 时， 我们认为 =0.

（1）用含 或 的代数式表示 及 ；

（2）求 与 的函数关系式，并求 的最大值和最小值．

（3）对给定的一个 值，有时只能确定唯一的点 ，指出这样的 的取值范围.

发现

请你确定一条直线，使得 三点到这条直线的距离之和最小（不必写出过程），并写出这个最小值.

23、（11分）如图，在平面直角坐标系中，直线 与抛物线 交于A，B两点，点A在 轴上，点B的纵坐标为3.点P是直线AB下方的抛物线上一动点 （不与A，B重合），过点P作 轴的垂线交直线AB与点C，作PD⊥AB于点D

（1）求 及 的值

（2）设点P的横坐标为

     ①用含 的代数式表示线段PD的长，

并求出线段PD长的最大值；

B

C

D

X

O

P

A

Y

两个三角形，是否存在适合的 值，

使这两个三角形的面积之比为9:10？

若存在，直接写出 值；若不存在，说明理由.

28．(本题10分)

    已知：在△ABC中，∠ACB=900，点P是线段AC上一点，过点A作AB的垂线，交BP的延长线于点M，MN⊥AC于点N，PQ⊥AB于点Q，A0=MN．

    (1)如图l，求证：PC=AN；

    (2)如图2，点E是MN上一点，连接EP并延长交BC于点K，点D是AB上一点，连接DK，∠DKE=∠ABC，EF⊥PM于点H，交BC延长线于点F，若NP=2，PC=3，CK：CF=2：3，求DQ的长．

28．（本小题满分10分）

    如图，在平面直角坐标系中，已知Rt△AOB的两条直角边OA、OB分别在y轴和x轴上，并且OA、OB的长分别是方程x2－7x＋12=0的两根（OA＜OB），动点P从点A开始在线段AO上以每秒1个单位长度的速度向点O运动；同时，动点Q从点B开始在线段BA上以每秒2个单位长度的速度向点A运动，设点P、Q运动的时间为t秒.

（1）求A、B两点的坐标.

（2）求当t为何值时，△APQ与△AOB相似，并直接写出此时点Q的坐标.

（3）当t=2时，在坐标平面内，是否存在点M，使以A、P、Q、M为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由.

第28题图

28.如图，四边形ABCD为矩形，C点在x轴上，A点在y轴上，D点坐标是（0，0），B点坐标是（3，4），矩形ABCD沿直线EF折叠，点A落在BC边上的G处，E、F分别在AD、AB上，且F点的坐标是（2，4）．
（1）求G点坐标；
（2）求直线EF解析式；
（3）点N在x轴上，直线EF上是否存在点M，使以M、N、F、G为顶点的四边形是平行四边形？若存在，请直接写出M点的坐标；若不存在，请说明理由．

24．如图，抛物线y=ax2+bx+2交x轴于A（﹣1，0），B（4，0）两点，交y轴于点C，与过点C且平行于x轴的直线交于另一点D，点P是抛物线上一动点．

（1）求抛物线解析式及点D坐标；

（2）点E在x轴上，若以A，E，D，P为顶点的四边形是平行四边形，求此时点P的坐标；

（3）过点P作直线CD的垂线，垂足为Q，若将△CPQ沿CP翻折，点Q的对应点为Q′．是否存在点P，使Q′恰好落在x轴上？若存在，求出此时点P的坐标；若不存在，说明理由．

26．如图，在矩形OABC中，AO=10，AB=8，沿直线CD折叠矩形OABC的一边BC，使点B落在OA边上的点E处．分别以OC，OA所在的直线为x轴，y轴建立平面直角坐标系，抛物线 经过O，D，C三点．

（1）求AD的长及抛物线的解析式；12999数学网 www.12999.com

（2）一动点P从点E出发，沿EC以每秒2个单位长的速度向点C运动，同时动点Q从点C出发，沿CO以每秒1个单位长的速度向点O运动，当点P运动到点C时，两点同时停止运动．设运动时间为t秒，当t为何值时，以P、Q、C为顶点的三角形与△ADE相似？

（3）点N在抛物线对称轴上，点M在抛物线上，是否存在这样的点M与点N，使以M，N，C，E为顶点的四边形是平行四边形？若存在，请直接写出点M与点N的坐标（不写求解过程）；若不存在，请说明理由．

25、已知四边形ABCD是正方形，O为正方形对角线的交点，一动点P从B开始，沿射线

BC运到，连结DP，作CN⊥DP于点M，且交直线AB于点N，连结OP，ON。（当P在线段BC上时，如图9：当P在BC的延长线上时，如图10）

 （1）请从图9，图10中任选一图证明下面结论：

        ①BN=CP：    ②OP=ON，且OP⊥ON

  (2)  设AB=4，BP= ，试确定以O、P、B、N为顶点的四边形的面积 与 的函数关系。

24．（本小题满分10分）[来源:学.科.网]

图8

（1）求抛物线 的解析式；

（2）设抛物线 与 轴的另一个交点为 ,点 是线段 上一个动点（ 不与 重合），过点 作 轴的垂线，垂足为 ,连接 .如果 点的坐标为 , 的面积为S，求S与 的函数关系式，写出自变量 的取值范围，并求出S的最大值；

（3）设抛物 线 的对称轴与 轴的交点为 ，以 为圆心， 两点间的距离为直径作⊙ ，试判断直线 与⊙ 的位置关系，并说明理由.

26．我们常见的炒菜锅和锅盖都是抛物线面，经过锅心和盖心的纵断面是两端抛物线组合而成的封闭图形，不妨简称为“锅线”，锅口直径为6dm，锅深3dm，锅盖高1dm（锅口直径与锅盖直径视为相同），建立直接坐标系如图①所示，如果把锅纵断面的抛物线的记为C1 ，把锅盖纵断面的抛物线记为C2．

（1）求C1和C2的解析式；

（2）如图②，过点B作直线BE：y= x﹣1交C1于点E（﹣2，﹣ ），连接OE、BC，在x轴上求一点P，使以点P、B、C为顶点的△PBC与△BOE相似，求出P点的坐标；

（3）如果（2）中的直线BE保持不变，抛物线C1或C2上是否存在一点Q，使得△EBQ的面积最大？若存在，求出Q的坐标和△EBQ面积的最大值；若不存在，请说明理由．

28.如图，菱形ABCD的边长为2cm，∠DAB=60°．点P从A点出发，以 cm/s的速度，沿AC向C作匀速运动；与此同时，点Q也从A点出发，以1cm/s的速度，沿射线AB作匀速运动．当P运动到C点时，P、Q都停止运动．设点P运动的时间为ts．

（1）当P异于A．C时， 请说明PQ∥BC；

（2）以P为圆心、PQ长为半径作圆，请问：在整个运动过程中，t为怎样的值时，⊙P与边BC分别有1个公共点和2个公共点 ？

28．（本题满分12分）

在平面直角坐标系中,已知二次函数的图象经过点和点,直线经过抛物线的顶点且与轴垂直,垂足为.

(1)  求该二次函数的表达式；

(2)  设抛物线上有一动点从点 处出发沿抛物线向上运动,其纵坐标 随时间

≥ )的变化规律为 .现以线段为直径作.

①当点 在起始位置点 处时,试判断直线 与的位置关系,并说明理由；在点 运动的过程中,直线 与是否始终保持这种位置关系? 请说明你的理由；

②若在点 开始运动的同时,直线 也向上平行移动,且垂足 的纵坐标 随时间 的变化规律为 ,则当在什么范围内变化时,直线与相交? 此时,若直线被所截得的弦长为 ,试求 的最大值.

第28题备用图

·

A

B

O

1

2

x

y

l

Q

第28题图

·

A

B

O

1

2

x

y

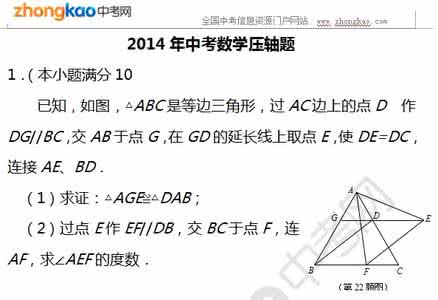
26.如图，已知抛物线经过原点O和  轴上一点A（4，0），抛物线顶点为E，它的对称轴

   与  轴交于点D.直线            经过抛物线上一点B（-2，m）且与  轴交于点C，

   与抛物线的对称轴交于点F.

  （1）求m的值及该抛物线对应的解析式；

  （2）P      是抛物线上的一点，若S△ADP=S△ADC,求出所有符合条件的点P的坐标；

  （3）点Q是平面内任意一点，点M从点F出发，沿对称轴向上以每秒1个单位长度的速度匀速运动，设点M的运动时间为t秒，是否能使以Q、A、E、M四点为顶点的四边形是菱形.若能，请直接写出点M的运动时间t的值；若不能，请说明理由.

28.如图14，已知点 点C在y轴的正半轴上，且 抛物线

经过 三点，其顶点为 .

(1)求抛物线 的解析式；

(2)试判断直线CM与以AB为直径的圆的位置关系，并加以证明；

(3)在抛物线上是否存在点N，使得 ?如果存在，那么这样的点有几个？如果存在，那么这样的点有几个？如果不存在，请说明理由。

24．(12分)如图，在△ABC中，∠C＝90o，AC＝6cm，BC＝8cm，D、E分别是AC、AB的中点，连接DE．点P从点D出发，沿DE方向匀速运动，速度为1cm/s；同时，点Q从点B出发，沿BA方向匀速运动，速度为2cm/s，当点P停止运动时，点Q也停止运动．连接PQ，设运动时间为t(0＜t＜4)s．解答下列问题：

(1)当t为何值时，PQ⊥AB？

(2)当点Q在B、E之间运动时，设五边形PQBCD的面积为ycm2，求y与t之间的函数关系式；

(3)在(2)的情况下，是否存在某一时刻t，使得PQ分四边形BCDE所成的两部分的面积之比为S△PQE∶S五边形PQBCD＝1∶29？若存在，求出此时t的值以及点E到PQ的距离h；若不存在，请说明理由．

25.(本题满分10分)

如图，在平面直角坐标系中，将一块等腰直角三角板 斜靠在两坐标轴上放在第二象限 ，点C的坐标为 ． 点在抛物线 的图象上，过点 作 轴，垂足为 ，且 点横坐标为 ．

（1）求证： ；

（2）求 所在直线的函数关系式；

A

B

D

C

O

x

y

(第25题图)

[来源:Z.xx.k.Com]

26．（2012山西）综合与实践：如图，在平面直角坐标系中，抛物线y=﹣x2+2x+3与x轴交于A．B两点，与y轴交于点C，点D是该抛物线的顶点．

（1）求直线AC的解析式及B．D两点的坐标；

（2）点P是x轴上一个动点，过P作直线l∥AC交抛物线于点Q，试探究：随着P点的运动，在抛物线上是否存在点Q，使以点A．P、Q、C为顶点的四边形是平行四边形？若存在，请直接写出符合条件的点Q的坐标；若不存在，请说明理由．

（3）请在直线AC上找一点M，使△BDM的周长最小，求出M点的坐标．

28． (本小题满分l2分)

    如图，在平面直角坐标系xOy中，一次函数 ( 为常数)的图象与x轴交于点A(，0)，与y轴交于点C．以直线x=1为对称轴的抛物线  ( 为常数，且 ≠0)经过A，C两点，并与x轴的正半轴交于点B．

   （1）求 的值及抛物线的函数表达式；

   （2）设E是y轴右侧抛物线上一点，过点E作直线AC的平行线交x轴于点F．是否存在这样的点E，使得以A，C，E，F为顶点的四边形是平行四边形？若存在，求出点E的坐标及相应的平行四边形的面积；若不存在，请说明理由；

  （3）若P是抛物线对称轴上使△ACP的周长取得最小值的点，过点P任意作一条与y轴不平行的直线交抛物线于 ， 两点，试探究 是否为定值，并写出探究过程．

24．在平面直角坐标xOy中，（如图）正方形OABC的边长为4，边OA在x轴的正半轴上，边OC在y轴的正半轴上，点D是OC的中点，BE⊥DB交x轴于点E．

（1）求经过点D、B、E的抛物线的解析式；

（2）将∠DBE绕点B旋转一定的角度后，边BE交线段OA于点F，边BD交y轴于点G，交（1）中的抛物线于M（不与点B重合），如果点M的横坐标为 ，那么结论OF= DG能成立吗？请说明理由；

（3）过（2）中的点F的直线交射线CB于点P，交（1）中的抛物线在第一象限的部分于点Q，且使△PFE为等腰三角形，求Q点的坐标．

24．如图所示，在形状和大小不确定的△ABC中，BC=6，E、F分别是AB．AC的中点，P在EF或EF的延长线上，BP交CE于D，Q在CE上且BQ平分∠CBP，设BP=y，PE=x．

（1）当x= EF时，求S△DPE：S△DBC的值；

（2）当CQ= CE时，求y与x之间的函数关系式；

（3）①当CQ= CE时，求y与x之间的函数关系式；

     ②当CQ= CE（n为不小于2的常数）时，直接写出y与x之间的函数关系式

24．（2012宜宾）如图，在△ABC中，已知AB=AC=5，BC=6，且△ABC≌△DEF，将△DEF与△ABC重合在一起，△ABC不动，△ABC不动，△DEF运动，并满足：点E在边BC上沿B到C的方向运动，且DE、始终经过点A，EF与AC交于M点．

（1）求证：△ABE∽△ECM；

（2）探究：在△DEF运动过程中，重叠部分能否构成等腰三角形？若能，求出BE的长；若不能，请说明理由；

（3）当线段AM最短时，求重叠部分的面积．

24．如图1，已知菱形ABCD的边长为 ，点A在x轴负半轴上，点B在坐标原点．点D的坐标为（- ，3），抛物线y=ax2+b（a≠0）经过AB、CD两边的中点．

（1）求这条抛物线的函数解析式；

（2）将菱形ABCD以每秒1个单位长度的速度沿x轴正方向匀速平移（如图2），过点B作BE⊥CD于点E，交抛物线于点F，连接DF、AF．设菱形ABCD平移的时间为t秒（0＜t＜ 3 ）

①是否存在这样的t，使△ADF与△DEF相似？若存在，求出t的值；若不存在，请说明理由；

②连接FC，以点F为旋转中心，将△FEC按顺时针方向旋转180°，得△FE′C′，当△FE′C′落在x轴与抛物线在x轴上方的部分围成的图形中（包括边界）时，求t的取值范围．（写出答案即可）

24．(2012?丽水)在△ABC中，∠ABC＝45°，tan∠ACB＝ ．如图，把△ABC的一边BC放置在x轴上，有OB＝14，OC＝ ，AC与y轴交于点E．[来源:Zxxk.Com]

(1)求AC所在直线的函数解析式；

(2)过点O作OG⊥AC，垂足为G，求△OEG的面积；

(3)已知点F(10，0)，在△ABC的边上取两点P，Q，是否存在以O，P，Q为顶点的三角形与△OFP全等，且这两个三角形在OP的异侧？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．

25．如图，矩形OABC的两边在坐标轴上，连接AC，抛物线 经过A，B两点。

（1）求A点坐标及线段AB的长；

（2）若点P由点A出发以每秒1个单位的速度沿AB边向点B移动，1秒后点Q也由点A出发以每秒7个单位的速度沿AO，OC，CB边向点B移动，当其中一个点到达终点时另一个点也停止移动，点P的移动时间为t秒。

①当PQ⊥AC时，求t的值；

②当PQ∥AC时，对于抛物线对称轴上一点H，∠HOQ＞∠POQ，求点H的纵坐标的取值范围。

26．已知：如图，在直角梯形ABCD中，AD∥BC，∠B=90°，AD=2，BC=6，AB=3．E为BC边上一点，以BE为边作正方形BEFG，使正方形BEFG和梯形ABCD在BC的同侧．

（1）当正方形的顶点F恰好落在对角线AC上时，求BE的长；

（2）将（1）问中的正方形BEFG沿BC向右平移，记平移中的正方形BEFC为正方形B′EFG，当点E与点C重合时停止平移．设平移的距离为t，正方形B′EFG的边EF与AC交于点M，连接B′D，B′M，DM，是否存在这样的t，使△B′DM是直角三角形？若存在，求出t的值；若不存在，请说明理由；

（3）在（2）问的平移过程中，设正方形B′EFG与△ADC重叠部分的面积为S，请直接写出S与t之间的函数关系式以及自变量t的取值范围．

爱华网本文地址 » http://www.aihuau.com/a/405851/696544971379.html