摘要:针对分段迭代曲线拟合存在的重建区域轮廓不连续、重建区域尺寸有误差等问题,提出了一种基于融合细分的纹理图像重构模型。首先提取原始图像的分割区域,经过轮廓跟踪与下采样得到区域形状的特征向量;然后利用三重逼近与三重插值统一的融合细分方法,重建区域轮廓曲线;最后合成区域纹理,得到纹理图像重构结果。在多幅自然场景图像上进行实验验证,并给出相应的实验结果和分析。实验结果表明,所提模型正确有效,具有和人类视觉特性相符合的重构结果; 所提算法能够减少图像重建时的处理时间,并在图像质量主观评价指标上明显优于多区域图像重建算法。
关键词:纹理图像重构;融合细分;纹理合成;图像分割
一、引言
随着数字多媒体技术的发展,人们对高效的图像信息处理提出了更高的要求。现有的基于像素/块的图像处理技术忽略了图像的层级结构,无法直接用于内容分析;而基于对象的又难以满足图像处理在通用性方面的需求[1]。因此,如何找到一种更加有效的图像表征方法一直是图像处理领域的研究热点与难点问题。
纹理是表达图像内容的一个非常重要的属性,它广泛存在于各类图像中。纹理图像通常构成图像或视频的静止背景。图像中的纹理分为两大类:不重要主观细节纹理和重要主观细节纹理[2]。由于人类视觉系统固有的缺陷,人眼对平滑区域的敏感性远高于纹理密集区域,图像中的纹理通常是人眼不关注的那部分内容,因此纹理细节的变化不会影响对原始纹理的主观理解[3]。
近年来,基于样图的纹理合成在图像修复、压缩编码、纹理传输等方面有着广泛的应用[4-6]。Efros等[7]提出一种计算较简单的Image Quilting算法,通过计算纹理重叠区域的累积误差和最小误差路径进行纹理拼接。而旋转的Wang Tiles 纹理合成算法[8]能够克服Wang Tiles 存在的样图利用不完全、切割路径非最优、中心和拐角区域不匹配等缺点。
图像中的线结构是指用来定义目标形状的轮廓或划分区域的边界,是图像的形状特征表达[9-10]。早期的形状描述方法使用二进制图像,基于二进制边缘的方法有很多,例如多边形近似、曲率的频域表示等。Zhang等[11]系统阐述了两类图像形状的表示算法:一类是基于轮廓,另一类是基于区域。每一类形状表示算法可分为结构方法和全局方法,并适用于空域和变换域。
利用图像的线结构与纹理特性,文献[12]提出了一种基于分段迭代曲线拟合的多区域图像重建算法。包含了大量纹理的多区域重建结果用于构建图像或视频的静止背景,而图像的前景是骏马、苍鹰或美女等,视频的前景是飞驰的猎豹、飞翔的苍鹰或游泳的美女等。由人类视觉系统的感知特性可知,人眼的视觉注意力主要集中于上述前景,而静止背景的视觉关注度是低的,尤其是纹理静止背景[12]。基于线结构和纹理特性的图像重建方法适用于构建图像与视频的静止背景图像。
但是,利用分段迭代曲线拟合重建的区域轮廓曲线是不连续的,需使用膨胀算法进行修复,从而造成重建区域的尺寸存在误差,因此会引起重建质量差的问题。针对上述问题,提出利用三重逼近与三重插值统一的融合细分方法,重建区域轮廓曲线;将合成的区域纹理填充到重建的区域轮廓曲线中,从而得到纹理图像重构结果。实验结果表明本文算法重构的图像质量良好,图像质量的主观评价指标明显优于多区域图像重建算法。
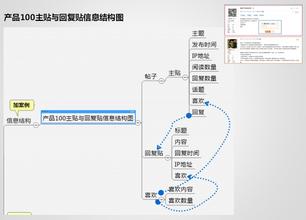
图1是本文提出的基于融合细分的纹理图像重构模型结构流程,主要包括预处理、融合细分和重构纹理图像3个阶段。
预处理阶段首先利用图像分割与区域融合方法获得原始纹理图像的多个区域及其索引号;然后通过轮廓跟踪与下采样,获得代表区域轮廓结构特征的有序序列。
融合细分阶段利用三重逼近与三重插值统一的融合细分方法,重建区域轮廓曲线。
重构纹理图像阶段首先,得到包含区域纹理局部与全局特征的区域纹理样本;然后,利用基于样图的纹理合成算法合成区域纹理;最后,将合成的区域纹理填充到重建的区域轮廓曲线中,实现纹理图像重构。
1.1预处理
首先,原始图像被分割为许多包含同质颜色与纹理特征的小分割区域[13-14],同时考虑到纹理样本选择对分割结果是敏感的,空间紧邻的小分割区域必须合并成较大的区域,每个区域获得一个唯一的索引号。
然后,利用轮廓跟踪算法[10-11]得到一个由区域边界曲线上的像素点组成的有序序列,按照随机间隔进行有序抽样即下采样提取,得到代表区域轮廓形状的特征向量(xs,ys),其中s是向量元素在区域轮廓曲线上的位置序号。
1.2融合细分
为了得到插值与逼近统一的融合细分方法,本文用新的角度观察三重逼近细分。
首先设定初始控制顶点P0i(i=1,2,…,n);其次在P0i和P0i+1之间的1/3和2/3处分别插入两个新的顶点P03i+1和P03i+2:
P03i+1=23P0i+13P0i+1
P03i+2=13P0i+23P0i+1(1
然后定义位移Δi如下所示:
Δi=-127P0i-1+227P0i-127P0i+1(2
将P03i+1和P03i+2分别移到新位置P13i+1和P13i+2,位移分别是Δi和Δi+1;同时将P03i移到新位置P13i,其位移恰好是4Δi。根据上述步骤,经过k次修改后,可得到一组新的控制顶点Pk+1。因此,三重逼近细分的递推公式可归纳为:
Pk+13i=Pki-4Δki
Pk+13i+1=23Pki+13Pki+1-Δki
Pk+13i+2=13Pki+23Pki+1-Δki+1 (3
基于上述三重逼近细分的推导方法,可推出新的三重插值细分。首先,保持控制网格中P0i固定不动;然后,将新插入的顶点P03i+1和P03i+2移到新位置P13i+1和P13i+2,位移分别为Δ′3i+1和Δ′3i+2,其位移方向恰好与三重逼近细分的顶点位移方向相反。Δ′3i+1和Δ′3i+2通过线性加权组合得到,并且满足细分曲线的收敛性和光滑性[15-16],定义如下:
Δ′3i+d=ωΔi+d-1+υΔi+2-d; d=1,2 (4)
其中:ω=32(1+μ),υ=32(1-μ), μ是自由参数。
 爱华网
爱华网