xiangliangzhi jifen
向量值积分
vector value integration
普通(数值的)积分在向量值上的推广。在分析数学的各分支中,因不同的要求,需要种种或是向量值函数的积分或是关于向量值测度的积分。向量值函数的积分有黎曼-斯蒂尔杰斯型积分和勒贝格型积分。
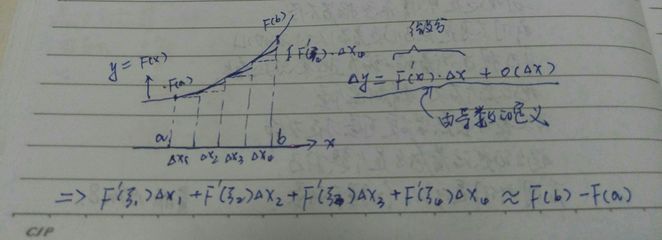
黎曼-斯蒂尔杰斯型积分 常用的一种向量值积分。如果()[kg2]是定义在[,]上,但取“值”于拓扑线性空间的函数,[kg1]则称()是[,]上向量值函数。设()和()[kg2]分别是[,]上向量值和数值函数。任取[,]上分点组:[772-3],作和式[772-22] [772-111][772-4]其中[772-5]令[772-6][772-222]如果极限[772-7]存在,则称关于在[,]上R-S可积,又称[772-8]是关于的黎曼-斯蒂尔杰斯积分,简称R-S积分,记为[772-9]。类似地,也可以引入[772-10]。向量值R-S积分有许多类似于数值函数的R-S积分的性质。特别,有分部积分公式:如果[772-11]中有一个存在,则另一个必存在,[kg2]且[772-12][772-333]。
下面几种向量值积分都属于勒贝格型的。
博赫纳积分 设(,,[kg2])是全有限测度空间(见测度论),()是定义在上,取值于巴拿赫空间的向量值函数如果存在 (,)的有限个互不相交的可测集, , …,,使在(=1,2,…,)上的值恒为向量,[kg2]而[772-21]上的值恒为0,则称是(向量值)简单函数。如果存在 上的一列简单函数 {()},使得‖()-()‖关于几乎处处收敛于0,则称()是上(取值于)的强可测函数。强可测函数 ()的范数‖()‖必是上的(数值)可测函数。如果是简单函数并且()是的博赫纳积分,记为[772-14]。设()是[kg2]上向量值函数,如果存在一个可积的简单函数列{},使得[772-15],就称是上博赫纳可积的,并称[772-16]是在上的博赫纳积分,记为[772-17],可以证明:对于博赫纳可积函数,它的积分值(是向量)不依赖于{}的选取;在上是博赫纳可积的,当且仅当是强可测的而且‖()‖是 上的数值可积函数。博赫纳积分具有一般测度论中积分的性质。
伯克霍夫积分 设(,,)[kg2]是全有限测度空间,{}是的一列互不相交的可测集,[772-444]并且[772-18],称{}是的可列剖分。设()是上取值于巴拿赫空间的向量值函数,[kg2]={}是的可列剖分,如果在每个上有界,并且
[772-19]是无条件收敛的,则称集[772-20]的凸闭包是()关于[kg2]的积分值域,记为(,)。如果对任何>0,存在可列剖分(),使集(,())的直径小于,则称[kg2]在上伯克霍夫可积,并称由一切可列剖分所得的[kg2](,)的交集(只有一个向量)为 在上的伯克霍夫积分,记为[773-1]。这种积分除富比尼定理外,具有通常勒贝格积分所具有的线性、可列可加性、绝对连续性等性质。博赫纳可积必然伯克霍夫可积(逆命题并不成立),并且两个积分相等。
更一般地,还可定义取值于具有某种拓扑结构半群上的积分,当取不同拓扑时,它可包含伯克霍夫积分和下面的积分。
盖尔范德意义下的弱积分 [kg2]设(,,)是全有限测度空间,()是定义在上取值于巴拿赫空间的向量值函数如果对每个(是的共轭空间),(())是可测函数,则称()在上是弱可测的在空间是可分情况下,弱可测和强可测一致如果对每个[772-555]在上是可积的,则必存在(,使得[773-2],称(是()在 X上的盖尔范德意义下的弱积分,记为[773-4]。
佩蒂斯积分 或称弱积分。另一种常用的向量值积分。设(,,)是全 有限测度空间,()是上取值于巴拿赫空间的弱可测函数,如果存在[kg1][kg1] 使得对一切[kg2][kg2]成立[773-5],则称在上是佩蒂斯可积的,是的佩蒂斯积分,记为[773-6]。博赫纳可积必然佩蒂斯可积,并且积分相等。除去富比尼定理外,勒贝格积分的其他性质对于佩蒂斯积分也成立。
向量值测度和积分 设(,)是可测空间,如果是定义在上取值于巴拿赫空间 的满足下列条件的向量值集函数:①()=0(是空集);②可列可加性,对中任何一列互
不相交的集{},
[773-7]则称 是上向量值测度。例如,如果(,,)是全有限测度空间,是上取值于巴拿赫空间的博赫纳可积函数,对任何[kg1][kg1],定义[773-8],[kg2]则便是上取值于的向量值测度。特别,当是某个巴拿赫空间(或希尔伯特空间)上的有界线性算子全体按算子范数所成的巴拿赫空间时,就称为上的算子值测度(见谱论、谱算子)。此外,和数值测度一样,也可引入一个向量值测度关于另一个数值测度绝对连续的概念。但一般说来没有拉东-尼科迪姆定理。但如果空间或是自反,或是希尔伯特空间,或的共轭空间是可分的,这时就有拉东-尼科迪姆定理。(见测度论)
杨亚立

以上就是网友分享的关于"向量值积分"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网