apei'er fangcheng
阿佩尔方程
Appell equation
法国数学家 P.-.阿佩尔导出的适用于非完整系统的重要动力学方程,其形式为:
[1-11] (1)式中为吉布斯函数,它是加速度动能式[1-12]用准加速度( =1,2,…, )表示之式;[2s]为对应于准坐标的广义力;是系统的自由度。由于完整系统是非完整系统的特例,因此,凡是适用于非完整系统的动力学方程,亦适用于完整系统。
假定一个有个质点的非完整系统,它含个有限约束
[2-11]和个微分约束
[2-12]。 (2)可先利用有限约束,将3个用 =3-个广义坐标,,…,表示,个微分约束用和(=1,2,…,)表示。由此可变换式(2)为:
[2-13], (3)式中个(=1,2,…,)只有(=-)个是独立的为了更一般化,采用个的线性式组成个准速度来描述这系统,即
[2-03]。由于非完整系统的微分约束(3)是不可积的,所以坐标不一定存在,这就是是准坐标名称的由来。的时间导数称为准加速度。 由于式(1)左边是对的偏导数,所以中一切不含的项都可以舍去不写,从而使计算函数的工作量大为减少。
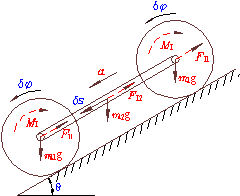
圆球、圆轮在粗糙面上无滑动地滚动,溜冰鞋在冰上的滑行等都是非完整系统力学问题的例子。
参考书目
W.D.MacMillan,Dynamics of Riid Bodies,McGraw-Hill,New York,1936.
E.T.Whittaker, A Treatise on the Analytical Dynamicsof Particles and Riid Bodies,4th ed.,Cambridge Univ.Press,Cambridge,1952.
汪家编:《分析力学》,高等教育出版社,北京,1983。
'" class=writer>汪家
以上就是网友分享的关于"阿佩尔方程"的相关资料,希望对您有所帮助,感谢您对爱华网的支持!
 爱华网
爱华网