[学习目标]
1. 掌握直角三角形中的边角关系
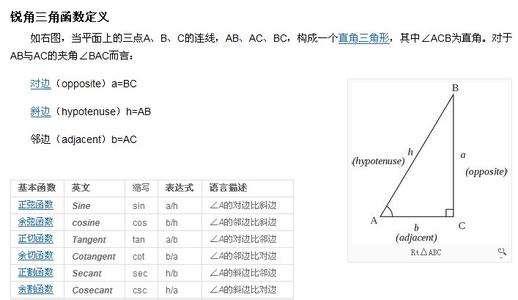
(1)三边之间的关系 (勾股定理)
(2)锐角之间的关系
(3)边角之间的关系 锐角三角函数
2. 理解解直角三角形的概念:直角三角形中,除直角外,一共有五个元素,即三条边和两个锐角。由直角三角形中的两个已知元素(直角除外且其中至少一个是边),求出其余未知元素的过程,叫解直角三角形。
3. 明确解直角三角形四类基本问题的方法
(1)已知斜边和一直角边(如斜边c,直角边a),由
求A,进而
(2)已知斜边和一锐角(如斜边c,锐角A),
(3)已知一直角边和一锐角(如a,A),
(4)已知两直角边(如a,b),,由,求A。
进而
3. 掌握解直角三角形的思路
(1)当已知或求解式中有斜边时,可用正弦或余弦;无斜边时,就应用正切或余切;当所求元素既可用乘法又可用除法时,则用乘法,不用除法;既可由已知数据又可用中间数据求解时,则取原始数据,忌用中间数据。
(2)当已知直角三角形中中线、高、角平分线、周长、面积等时,一般将这些元素转化为三角形中的元素或元素间的关系式,再通过解直角三角形的基本方法进行求解。
4. 理解掌握直角三角形中边、角之间的关系,会运用勾股定理,直角三角形的两锐角互余及锐角三角函数解直角三角形。
[学习重点、难点]
本节重点是在归纳直角三角形中边、角关系的基础上,利用这些关系式和上节概念解直角三角形。并利用三角形,四边形与解直角三角形的联系解实际问题。
难点是对解三角形方法的灵活选择应用。
【典型例题】
例1. 如图,在中,,求BC的长。
解:过A作于D
在中,
中,
点悟:过A作于D点,形成直角三角形来解题。
例2. 已知:如图,中,,于点D,交AB于点E,,连结CE。求的周长。
解:
为等腰直角三角形
在和中,
又
的周长
点悟:此题图形虽然较复杂,但所出现的四个三角形均为直角三角形,且有两个为等腰直角三角形,用逐一推理方法,不难求出的三边,于是可求其周长。
例3. 一个三角形的两边长分别为3cm和12cm,夹角为,和它面积相等的等腰直角三角形的斜边长是多少?
解:设等腰直角三角形的直角边长为xcm,则由题意,
由勾股定理,得斜边长
等腰直角三角形的斜边长为6cm。
点悟:本题利用了很重要的面积公式,即“”。
例4. 在中,,,求AB和。
解:作,并与BA延长线交于D
在中,
在中,,
由勾股定理
点悟:由题意,可作的补角,做垂线,构造直角三角形是转化求解的关键。
例5. 已知,如图在四边形ABCD中,,,求AC的长。
(1) (2) (3)
解:解法1,图(1)延长AD,BC相交于E
在中,
,即
在中,由勾股定理
解法2:图(2)
作于G,于H
为矩形,
在中,
在中
在中,由勾股定理
解法3:图(3),延长AB、DC相交于点F
在中,
在中,
在中,由勾股定理
点悟:本题的多解法中,我们可总结,特殊角要放在直角三角形中,使用起来才方便,无直角三角形时,一是可用等角代换,转移至直角三角形;二是可作垂线,构造直角三角形,对于常转化为其补角去发挥作用。
例6. 在中,为BC中点,,,求AB的长。
解:
设
在中,,由勾股定理
D是BC中点
在中,由勾股定理
的长是。
例7. 已知:如图在中,,BD是的平分线,,,求BC的长。
解:在中,
平分
设
在中,
BC长为。
例8. 已知:如图在直角梯形ABCD中,AB//CD,,E、F分别为AD、BC的中点,,求两底AB、CD的长。

解:过C作于G交EF于H
E、F分别是AD、BC的中点
在中,
为的中位线
答:AB长,CD长cm
点悟:本题使用“转化思想”,把分散的元素,通过添加辅助线,集中到一个三角形中,然后,再解此三角形。
【模拟试题】(答题时间:45分钟)
一. 选择题:
1. 已知在中,,则a等于( )
A. B. C. D. 3
2. 已知在中,三内角之比为,则三边之比等于( )
A. 1:2:3 B. 1::2 C. 1:3:4 D. 1::4
3. 等腰三角形底边上的高为8,周长为32,此三角形面积是( )
A. 56 B. 48 C. 40 D. 32
4. 已知如图菱形ABCD,对角线,那么等于( )
A. B. C. D.
5. 已知等腰三角形ABC中,一腰上高为1,这条高与底边夹角为,则的面积等于( )
A. 1 B. C. D.
二. 填空。
6. 若为锐角,且,则_______。
7. 在中,,则_______。
8. 已知直角三角形两直角边之和为,面积为2,则此直角三角形的斜边长为________。
9. 已知矩形的两条边长分别为和2,则这个矩形的两条对角线所夹的锐角度数为___________。
三. 解答题:
10. 如图(1)在中,的平分线,求及的值。
(1)
11. 已知,如图(2),在中,,CD是高,求证:
(2)
12. 平行四边形边长分别为,一个角为,求平行四边形两高的长。
【试题答案】
一. 1. D 2. B 3. B 4. A 5. A
二. 6. 7. 8. 4 9.
三. 10. 解:在中,
又是的平分线
11. 证明:设则
,
12. 解:在平行四边形ABCD中,
则
作于F,在中,
作于E,在中
答:此平行四边形的两高分别是与。
【励志故事】
乘静而入
菲律宾有家餐馆生意一直很清淡,这家餐馆老板特意到周围的餐馆光顾一番后发现:这些餐馆清一色的现代装饰,使气氛格外火爆,食客不少。于是这位老板就反其道而行之,决定突出本餐馆与众不同的古朴、幽静的独家特色:
室内是白色房柱,座席被绿色植物簇拥,用印度的古战车送菜,莎士比亚时代的酒桶盛酒……此举一出,餐馆生意立马击败所有对手,迅速走红。
 爱华网
爱华网