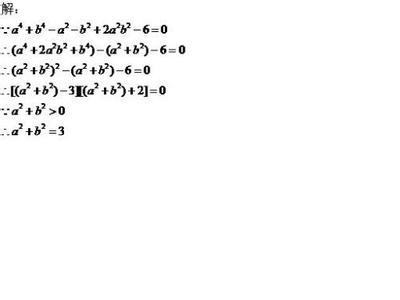直线的方程、两条直线的位置关系
二. 教学重、难点:
1. 理解直线的倾斜角和斜率的概念,掌握过两点的直线的斜率公式,掌握直线方程的点斜式、两点式、一般式,并能根据条件熟练地求出直线方程。
2. 掌握两条直线平行与垂直的条件,两条直线所成的角和点到直线的距离公式,能够根据直线的方程判断两条直线的位置关系。
【典型例题】
[例1] 已知点P到两个定点M(),N(1,0)距离的比为,点N到直线PM的距离为1,求直线PN的方程。
解:设点P的坐标为(x,y)
由题设有 即
∴ ① ∵ N到PM的距离为1,
∴ ∴ PM的方程为:②
②代入①: ∴
∴ P()或();或
∴ PN的方程为或
[例2] 已知的顶点A(3,4),B(6,0),C(),求的内角平分线AT所在的直线方程。
解:方法一:∵ 直线AC到AT的角等于AT到AB的角
又 ∵ ,
设AT的斜率为或,则
化简得,解之,得或(舍去)
∴ 直线AT的方程为
即所求的方程为
方法二:设直线AT上的动点P(x,y)则P点到AC、AB的距离相等
∵
∴ 直线AB的方程为,即
直线AC的方程为
即 那么
即或
结合图形分析知是的角A外角的平分线,故舍去。
∴ 所求的方程为
[例3] 的三个顶点分别为A(),B(2,1),C(),试分别求出:
(1)BC边所在直线的方程;
(2)BC边上的中线AD所在直线的方程;
(3)BC边的垂直平分线的方程。
解:(1)由题意,根据直线方程的两点式,可得BC边所在直线的方程为,即
(2)由题意,BC中点P的坐标为(0,2)又A(),可由直线方程的截距式求得中线AD所在直线的方程为,即。
(3)由题意,,其中点为(0,2),BC的垂直平分线的斜率为2,由直线方程的斜截式,求得直线方程为,即
[例4] 已知两直线,,当为何值时,与(1)相交;(2)平行;(3)重合?
解:当时, ∴
当m时,
∴ 与相交
当且时,由,得或
由,得
故(1)当,且时,与相交
(2)当或时,
(3)当时,与重合
[例5] 已知点P(2,),求:
(1)过P点与原点距离为2的直线的方程;
(2)过P点与原点距离最大的直线的方程,最大距离是多少?
(3)是否存在过P点与原点距离为6的直线?若存在,求出方程,若不存在,请说明理由。
解:(1)过P点的直线与原点距离为2,而P点坐标为(2,1),可见,过P(2,1)且垂直于轴的直线满足条件
此时的斜率不存在,其方程为
若斜率存在,设的方程为,即
由已知,得 解之,得
此时的方程为
综上,可得直线的方程为或
(2)作图可证过P点与原点O距离最大的直线是过P点且与PO垂直的直线,由,得
所以。由直线方程的点斜式得,即
故直线是过P点且与原点O距离最大的直线,最大距离为
(3)由(2)可知,过P点不存在到原点距离超过的直线,因此不存在过P点且到原点距离为6的直线
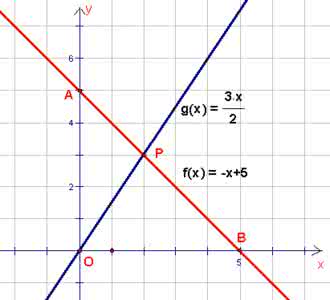
[例6] 已知函数,求的最小值,并求取得最小值时的值。
解:∵
它表示点P(x,0)与点A(1,1)的距离加上点P(x,0)与点B(2,2)的距离之和,即在轴上求一点P(x,0)与点A(1,1),B(2,2)的距离之和的最小值。
由图可知转化为求两点和间的距离,其距离为函数的最小值
∴ 的最小值为
再由直线方程的两点式得方程为
令,得 当时,的最小值为
[例7] 已知n条直线,…
(其中),这n条平行直线中,每相邻两条直线之间的距离顺次为2、3、4、…、n。
(1)求;
(2)求与轴、轴围成的图形的面积;
(3)求与及x轴、y轴围成的图形的面积。
解:(1)原点O到的距离为1,原点O到的距离为1+2,…原点O到的距离为
∵ ∴
(2)设直线交x轴于M,交y轴于N,则面积
(3)所围成的图形是等腰梯形,由(2)知,则有
∴
∴ 所求面积为
[例8] 已知三条直线:(),直线:和直线:,且与的距离是。
(1)求a的值;
(2)求到的角
(3)能否找到一点P,使得P点同时满足下列三个条件:① P是第一象限的点;② P点到的距离是P点到的距离的;③ P点到的距离与P点到的距离之比是?若能,求P点坐标;若不能,请说明理由。
解:(1)即
∴ 与的距离 ∴
∴ ∵ ∴
(2)由(1),即 ∴ ,而的斜率
∴
∵ ∴
(3)设点P(),若P点满足条件②,则P点在与平行的直线:上,且 即或
∴ 或
若P点满足条件③,由点到直线的距离公式有
即 ∴ 或
由P在第一象限 ∴ 不可能
联立方程和
解得但不符合题意应舍去
解得
即为同时满足三个条件的点。
【模拟试题】
一. 选择题:
1. 曲线在点()处的切线方程为( )
A. B.
C. D.
2. 若点P(2,)为圆的弦AB的中点,则直线AB的方程为( )
A. B.
C. D.
3. 直线与两坐标轴所围成的三角形面积不大于1,那么的范围是( )
A. B. C. 且 D. 或
4. 已知平面上直线的方向向量,点O(0,0)和A(1,)在上的射影分别是和,则=,其中等于( )
A. B. C. 2 D.
5. 已知过点和的直线与直线平行,则m的值为( )
A. 0 B. C. 2 D. 10
6. 已知的顶点,B(6,4),重心H(5,2),则点C的坐标为( )
A. B. C. D.
7. 已知是直线上两点,则A、B两点间的距离是( )
A. B. C. D.
8. 已知两直线的方程分别为,,它们在坐标系中的位置如图所示,则( )
A.
B.
C.
D.
二. 解析题:
1. 若点A(),B(),直线过点P(1,1),且与线段AB相交,求直线的倾斜角及斜率的取值范围。
2. 过点M(0,1)作直线,使它被两已知直线,所截得的线段恰好被M所平分,求直线的方程。
3. 已知点A、B的坐标分别是,直线的方程为,问直线是否与线段AB相交?
4. 已知直线经过点P(3,1)且被两平行直线和截得的线段长为5,求直线的方程。
【试题答案】
一.
1. B
解析:,则,即曲线在点()处的切线的斜率为,又切点为(),∴ 所求切线方程为,即
2. A
解析:由圆的弦的性质,圆心O(1,0)与P点连线与AB垂直,由知,∴ 直线AB的方程为,即
3. C
解析:令得,令,得
∴ 三角形面积 又,即 ∴
又 ∵ 时不合题意,故选C
4. D
解析:如图所示,令过原点,与方向相反,排除A、C,验证D即可。
5. B
解析:,令,解得
6. B
解析:设点C的坐标为(6,y),由题意,知BH⊥AC,AH⊥BC,得
∴ C(6,)
7. B
8. C
解析:对于直线,令可得,斜率,直线,令,得<0,斜率,从图中可以看出,即,可得
二.
1. 解析:结合图象,知直线与线段AB有交点,只需直线从PB逆时针绕P转到直线PA,而,,在这个旋转过程中,的斜率由变化到无穷大,又由负无穷大变化到,所以斜率的范围是,倾斜角的范围是
2. 解析:设所求直线与的交点分别为M1、M2,由题意,M点是线段M1M2的中点
设,则
从而 解得
此时上有两点已知,故其方程为,即
3. 解析:设直线与直线AB相交于P(x,y),且点P分有向线段AB的比为
则 ∵ 点P在直线上 ∴
解得 ∴ 点P在BA延长线上
故直线与线段AB不相交
4. 解析:若直线的斜率不存在,则直线的方程为,此时与的交点分别为和,截得的线段长,符合题意
若直线的斜率存在,则设直线的方程为
解方程组 得
解方程组 得
由,得
解之,得,即所求的直线方程为,综上,可知所求的方程为或
 爱华网
爱华网