在2011年的湖南湘潭市中考试卷中有这样一道题:
如图一,直线交轴于A点,交轴于B点,过A、B两点的抛物线交轴于另一点C(3,0)。
图一
(1)求抛物线的解析式;
(2)在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由。
第二问求“在抛物线的对称轴上是否存在点Q,使△ABQ是等腰三角形?若存在,求出符合条件的Q点坐标;若不存在,请说明理由。”
等腰三角形是一种特殊的几何图形,特别是当等腰三角形和函数及动点问题结合到一起,会出现答案的不唯一性,中考命题人员对此类问题往往特别的青睐,而学生解答时常会出现漏解现象。如果利用分类思想,结合直观作图的手段进行分析解答,可以有效避免因思维不严密出现漏解的现象。下面结合本题重点介绍一下利用分类思想解答此类问题的技巧。
一、以静制动,找准切入点。
此类问题中虽然所涉及的点是运动的,但总有部分已知点是不变的,抓住这些不变的点,将其作为解题的突破口,采取以静制动的策略是解答此类类型题成功所在。在这道题中,因为已知点Q是对称轴上的一个动点,所以它的位置是变化的,则△ABQ不唯一。认真分析已知可发现点Q在对称轴上,因此它的横坐标不变。且△ABQ的边AB是确定不变的,这样可从线段AB入手,以AB作解决问题的切入点,来寻找点Q的具体位置。
二、分类讨论,作图击破。
等腰三角形的边分两类:一类是腰;另一类是底。在这里已知边AB既可以为腰,又可以为底。当AB为腰时,又分两种情况:一种情况为AB=AQ,即AB为腰,且点A为顶角的顶点;另一种情况为AB=BQ,即AB为腰,且点B为顶角的顶点。这样共有三种情况出现:
第一种情况:当AB为腰,且点A为顶角的顶点时,点Q在以点A为圆心AB长为半径的圆上(如图二)。
第二种情况:当AB为腰,且点B为顶角的顶点时,点Q在以点B为圆心AB长为半径的圆上(如图三)。
第三种情况:当AB为底时,点Q在线段AB的垂直平分线上(如图四)。
图二 图三
图四 图五
由图二可以看出,即在上又在对称轴上的点有两个,我们可以将其标记为点和(如图五)。
由图三可以看出,即在上又在对称轴上的点也有两个,我们可以将其标记为点和(如图六)。观察图像发现点在直线上,因此不能构成等腰三角形。
由图四可以看出,即在线段AB的垂直平分线上又在对称轴上的点有一个,我们可以将其标记为点(如图七)。
图六 图七
通过作图可以发现满足条件的点共有四个,可以根据已知依次求出这四个点的坐标。具体解答如下:
【答案】解:(1)略
(2)∵,
∴该抛物线的对称轴为x=1。
设点Q坐标为(1,m),
则,又。
当AB=AQ时(即第一种情况,图五),,
解得:,
∴Q点坐标为(1,)或(1,);
当AB=BQ时(即第二种情况,图六),,
解得:,
∴Q点坐标为(1,0)或(1,6),
又∵点(1,6)在直线上,
∴点A、B、Q在同一直线,不成立,
∴Q点坐标为(1,0)。
当AQ=BQ时(即第三种情况,图七),,

解得:,
∴Q点坐标为(1,1)。
∴抛物线的对称轴上是存在着点Q(1,)、(1,)、(1,0)、(1,1),使△ABQ是等腰三角形。
利用分类思想,通过直观作图,可以直接做出满足条件的所有的点,避免了思考不全面而出现漏解的现象,有效的解答了动点与等腰三角形为背景的综合性问题。
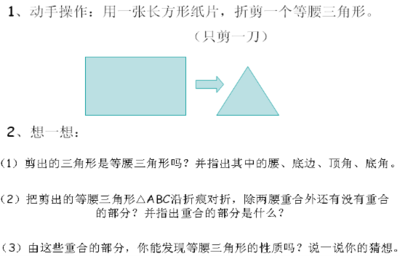
练一练:
1.(2010陕西省中考试题9题)如图八,点A、B、P在⊙O上的动点,要使△ABM为等腰三角形,则所有符合条件的点M有( )
A 1个 B 2个 C 3个 D 4个
图八 图九
2.(根据连云港市中考试题第28题改编)如图九,在平面直角坐标系中,O为坐标原点,⊙C的圆心坐标为(-2,-2),半径为.函数y=-x+2的图象与x轴交于点A,与y轴交于点B,点P为线段AB上一动点,若△POA是等腰三角形,求点P的坐标。
2011-11-09 人教网 爱华网
爱华网