时间:2006-4-11 17:38:00 来源:本站原创 作者:佚名
数学网继【小学数学趣题巧算百题百讲百练】系列后又最新推出【小学数学解题思路大全】系列!本系列包括式题的巧解妙算、巧想妙算文字题 、巧想妙算填充、判断、选择题、 巧想妙算数的基本知识题、巧解整除问题 、巧想妙算应用题、巧想妙算初步几何知识题等几部分,几乎囊括了所有类型的例题及解题思路。
数学网将会为广大数学爱好者、小学生和家长提供更多的资源。 欢迎大家提供意见和建议,积极参与,共同进步!
1.特殊数题(1)21-12
当被减数和减数个位和十位上的数字(零除外)交叉相等时,其差为被减数与减数十位数字的差乘以9。
因为这样的两位数减法,最低起点是21-12,差为9,即(2-1)×9。减数增加1,其差也就相应地增加了一个9,故31-13=(3-1)×9=18。减数从12—89,都可类推。
被减数和减数同时扩大(或缩小)十倍、百倍、千倍……,常数9也相应地扩大(或缩小)相同的倍数,其差不变。如
210-120=(2-1)×90=90,
0.65-0.56=(6-5)×0.09=0.09。
(2)31×51
个位数字都是1,十位数字的和小于10的两位数相乘,其积的前两位是十位数字的积,后两位是十位数字的和同1连在一起的数。
若十位数字的和满10,进1。如
证明:(10a+1)(10b+1)
=100ab+10a+10b+1
=100ab+10(a+b)+1
(3)26×86 42×62
个位数字相同,十位数字和是10的两位数相乘,十位数字的积与个位数字的和为积的前两位数,后两位是个位数的积。若个位数的积是一位数,前面补0。
证明:(10a+c)(10b+c)
=100ab+10c(a+b)+cc
=100(ab+c)+cc (a+b=10)。
(4)17×19
十几乘以十几,任意一乘数与另一乘数的个位数之和乘以10,加个位数的积。
原式=(17+9)×10+7×9=323
证明:(10+a)(10+b)
=100+10a+10b+ab
=[(10+a)+b]×10+ab。
(5)63×69
十位数字相同,个位数字不同的两位数相乘,用一个乘数与另个乘数的个位数之和乘以十位数字,再乘以10,加个位数的积。
原式=(63+9)×6×10+3×9
=72×60+27=4347。
证明:(10a+c)(10a+d)
=100aa+10ac+10ad+cd
=10a[(10a+c)+d]+cd。
(6)83×87
十位数字相同,个位数字的和为10,用十位数字加1的和乘以十位数字的积为前两位数,后两位是个位数的积。如
证明:(10a+c)(10a+d)
=100aa+10a(c+d)+cd
=100a(a+1)+cd(c+d=10)。
(7)38×22
十位数字的差是1,个位数字的和是10且乘数的个位数字与十位数字相同的两位数相乘,积为被乘数的十位数与个位数的平方差。
原式=(30+8)×(30-8)
=302-82=836。
(8)88×37
被乘数首尾相同,乘数首尾的和是10的两位数相乘,乘数十位数字与1的和乘以被乘数的相同数字,是积的前两位数,后两位是个位数的积。
(9)36×15
乘数是15的两位数相乘。
被乘数是偶数时,积为被乘数与其一半的和乘以10;是奇数时,积为被乘数加上它本身减去1后的一半,和的后面添个5。
=54×10=540。
55×15
(10)125×101
三位数乘以101,积为被乘数与它的百位数字的和,接写它的后两位数。125+1=126。
原式=12625。
再如348×101,因为348+3=351,
原式=35148。
(11)84×49
一个数乘以49,把这个数乘以100,除以2,再减去这个数。
原式=8400÷2-84
=4200-84=4116。
(12)85×99
两位数乘以9、99、999、…。在被乘数的后面添上和乘数中9的个数一样多的0、再减去被乘数。
原式=8500-85=8415
不难看出这类题的积:
最高位上的两位数(或一位数),是被乘数与1的差;
最低位上的两位数,是100与被乘数的差;
中间数字是9,其个数是乘数中9的个数与2的差。
证明:设任意两位数的个位数字为b、十位数字为a(a≠0),则
如果被乘数的个位数是1,例如
31×999
在999前面添30为30999,再减去30,结果为30969。
71×9999=709999-70=709929。
这是因为任何一个末位为1的两位自然数都可表示为(10a+1)的形式,由9组成的自然数可表示为(10n-1)的形式,其积为
(10a+1)(10n-1)=10n+1a+(10n-1)-10a。
(13)1÷19
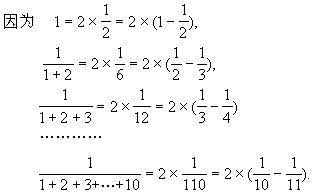
这是一道颇为繁复的计算题。
原式=0.052631578947368421。
根据“如果被除数不变,除数扩大(或缩小)若干倍,商反而缩小(或扩大)相同倍”和“商不变”性质,可很方便算出结果。
原式转化为0.1÷1.9,把1.9看作2,计算程序:
(1)先用0.1÷2=0.05。
(2)把商向右移动一位,写到被除数里,继续除
如此除到循环为止。
仔细分析这个算式:
加号前面的0.05是0.1÷2的商,后面的0.05×0.1÷1.9中0.05×0.1=0.005,就是把商向右移动一位写到被除数里,除以1.9。这样我们又可把除数看作2继续除,依此类推。
除数末位是9,都可用此法计算。
例如1÷29,用0.1÷3计算。
1÷399,用0.1÷40计算。
2.估算
数学素养与能力(含估算能力)的强弱,直接影响到人们的生活节奏和工作、学习、科研效率。已经引起世界有关专家、学者的重视,是个亟待研究的课题。
美国数学督导委员会,提出的12种面向全体学生的基本数学能力中,第6种能力即估算:“学生应会通过心算或使用各种估算技巧快速进行近似计算。当解题或购物中需要计算时,估算可以用于考查合理性。检验预测或作出决定……”
(1)最高位估算
只计算式中几个运算数字的最高位的结果,估算整个算式的值大概在什么范围。
例1 1137+5044-3169
最高位之和1+5-3=3,结果在3000左右。
如果因为忽视小数点而算成560,依据“一个不等于零的数乘以真分数,积必小于被乘数”估算,错误立即暴露。
例3 51.9×1.51
整体思考。
因为 51.9≈50,
而50×1.51≈50×1.5=75,
又51.9>50,1.51>1.5,
所以51.9×1.51>75。
另外9×1=9,
所以原式结果大致是75多一点,三位小数的末位数字是9。
例4 3279÷79
把3279和79,看作3200和80。准确商接近40,若相差较大,则是错的。
(2)最低位估算
例如,6403+232+1578
3+2+8=13,原式和的末位必是3。
(3)规律估算
和大于每一个加数;
两个真分数(或纯小数)的和小于2;
一个真分数与一个带分数(或一个纯小数与一个带小数)的和大于这个带分数(或带小数),且小于这个带分数(或带小数)的整数部分与2的和;
两个带分数(或带小数)的和总是大于两个带分数(或带小数)整数部分的和,且小于这两个整数部分的和加上2;
奇数±奇数=偶数,偶数±偶数=偶数,奇数±偶数=奇数;
差总是小于被减数;
整数与带分数(或带小数)的差小于整数与带分数(或带小数)的整数部分的差;带分数(或带小数),与整数的差大于带分数(或带小数)的整数部分与整数的差。
带分数(或带小数)与真分数(或纯小数)的差小于这个带分数(或带小数),且大于带分数(或带小数)减去1的差;
带分数与带分数(或带小数与带小数)的差小于被减数与减数的整数部分的差,且大于这个差减去1;
如果两个因数都小于1,则积小于任意一个因数;
若两个因数都大于1,则积大于任意一个因数;
带分数与带分数(或带小数与带小数)的积大于两个因数的整数部分的积,且小于这两个整数部分分别加1后相乘的积; 例如,
A<AB<B。
奇数×偶数=偶数,偶数×偶数=偶数;
若除数<1,则商>被除数;
若除数>1,则商<被除数;
若被除数>除数,则商>1;
若被除数<除数,则商<1。
(4)位数估算
整数减去小数,差的小数位数等于减数的小数位数;例如,320-0.68,差为两位小数。
最高位的乘积满十的两个整数相乘的积的位数,等于这两个数的位数和;
例如,451×7103
最高位的积4×7=28,满10,结果是3+4=7(位数)。在整除的情况下,被除数的前几位不够除,商的位数等于被除数的位数减去除数的位数;
例如,147342÷27
14不够27除,商是4-2=2(位数)。
被除数的前几位够除,商的位数等于被除数的位数与除数位数的差加上1。
例如,30226÷238
302够238除,商是5-3+1=3(位数)。
(5)取整估算
把接近整数或整十、整百、……的数,看作整数,或整十、整百…的数估算。
如1.98+0.97≈2+1,和定小于3。
12×8.5≈10×10,积接近100。
3.并项式
应用交换律、结合律,把能凑整的数先并起来或去括号。
例1 3.34+12.96+6.66
=12.96+(3.34+6.66)
=12.96+10=22.96
=3-3=0
例3 15.74-(8.52+3.74)
=15.74-3.74-8.52
=12-8.52=3.48
例4 1600÷(400÷7)
=1600÷400×7
=4×7
=28
 爱华网
爱华网