函数图象、函数的综合应用
二. 本周教学重、难点:
1. 掌握利用描点法和图象变换作出函数图象的一般方法;掌握函数图象变化的一般规律;能够利用函数的图象来观察分析函数的性质。
2. 掌握函数与其它数学知识,实际问题的综合,掌握数学模型的构造,函数关系式的建立。
【典型例题】
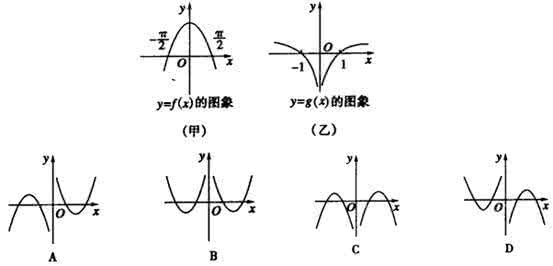
[例1] 设,二次函数的图象为下列之一,则的值为( )
A. 1 B. C. D.
解:∵ ∴ 不是前两个图形,从后两个图形看
∴ ,故应是第3个图形 ∵ 图象过原点 ∴ ,结合
∴
[例2] 在同一平面直角坐标系中,函数和的图象关于直线对称,现将的图象沿轴向左平移2个单位,再沿轴向上平移1个单位,所得到的图象是由两条线段组成的折线(如图所示),则函数的表达式为( )
A. B.
C. D.
解:由图象求得解析式将图象向右平移2个单位,向下平移1个单位得到图象
∴ ∵ 与的图象关于对称
∴ 与互为反函数
∴
[例3] 关于的方程恰有三个不相等的实数根,则实数的值是 。
解:原方程化为。作函数及的图象如图所示。由图可知当或时,两图象恰有三个交点,即原方程有三个实数解。
[例4] 某工厂生产某种产品,已知该产品的月产量(吨)与每吨产品的价格P(元/吨)之间的关系为P=24200,且生产吨的成本为R=50000+200元。问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入-成本)
解:设生产吨产品,利润为元
,
当每月生产200吨时利润最大,最大利润为3150000元。
[例5] 已知(),设,试确定实数的取值范围,使得对于一切大于1的正整数,不等式
恒成立。
解:由,得
∴
∴
∴
∴
要使对于一切大于1的正整数使原不等式恒成立,只需不等式
成立即可。
设,则
于是,解得
从而
解得且
∴ 实数的取值范围为且
[例6] 某厂生产一种仪器,由于受生产能力和技术水平的限制,会产生一些次品,根据经验知道该厂生产这种仪器次品率P与日产量(件)之间大体满足关系:
(其中为小于96的正常数)
注:次品率,如表示每生产10件产品,约有1件为次品。其余为合格品。
已知每生产一件合格的仪器可以盈利A元,但每生产一件次品将亏损元,故厂方希望定出合格的日产量。
(1)试将生产这种仪器每天的盈利额T(元)表示为日产量(件)的函数;
(2)当日产量为多少时,可获得最大利润?
解析:
(1)当时,P,所以每天的盈利额
当时,,所以每日生产的合格仪器约有件,次品约有件,故每天的盈利额
综上,日盈利额T(元)与日产量(件)的函数关系为
(2)由(1)知,当时,每天的盈利额为0
当时,
令,则
故
当且仅当,即(即)时等号成立。
所以①当时,(当且仅当时等号成立)
② 当时,由,得,易证函数
在(12,95)上单调递增(证明过程略)
所以
所以
即(当且仅当时等号成立)
综上,若,则当日产量为84件时,可获得最大利润;若,则当日产量为时,可获得最大利润。
[例7] 已知平面ABC,,垂足D在BC的延长线上,且BC=CD=DA=1,设PD=,,求的最大值。
解:设,,则
由面ABC,,易知(三垂线定理)
易求得,
∴ ()
由可先求得
故当,即时,取得最大值
[例8] 定义在R上的函数满足:如果对任意,都有
,则称是R上的凹函数。
已知二次函数(,且)
(1)求证:当时,函数为凹函数;
(2)如果时,,试求的取值范围。
解:
(1)证明:任取,则
∵ ∴
∴ 时,为凹函数
(2)(*)
当时,
当时,(*)式
当时,的最大值为的最小值为0
∴ 但 ∴
【模拟试题】
一. 选择题:
1. 为了得到函数的图象,只需把函数的图象上所有的点( )
A. 向右平移3个单位长度,再向下平移1个单位长度
B. 向左平移3个单位长度,再向下平移1个单位长度
C. 向右平移3个单位长度,再向上平移1个单位长度
D. 向左平移3个单位长度,再向上平移1个单位长度
2. 函数对一切实数都满足,有3个实根,则这3个实根之和为( )
A. 6 B. 9 C. 4 D. 3
3. 函数的图象是( )
4. 函数的图象大致是( )
5. 在直角梯形ABCD中,动点P从B点出发,由沿边运动,设点P的运动路程为,的面积为,如果函数的图象如图(2)所示,则的面积为( )
A. 10 B. 16 C. 18 D. 32
6. 由于电子技术的飞速发展,计算机的成本不断降低,若每隔3年计算机的价格降低,则现在价格为8100元的计算机9年后的价格为( )
A. 300元 B. 900元 C. 2400元 D. 3600元
7. 某公司在甲、乙两地销售一种品牌车,利润(单位:万元)分别为和,其中为销售量(单位:辆),若该公司在这两地共销售15辆车,则获得的最大利润为( )
A. 45.606 B. 45.6 C. 45.56 D. 45.51
8. 一个人以6米/秒的速度去追停在交通灯前的汽车,当他离汽车25米时,交通灯由红变绿,汽车以1米/秒2的加速度匀加速开走,那么( )
A. 人可在7米内追上汽车
B. 人可在10米内追上汽车
C. 人追不上汽车,他们之间距离最近为5米
D. 人追不上汽车,他们之间距离最近为7米
二. 解答题:
1. 已知二次函数的图象与轴交于A、B两点且,它在轴上截距为,对任意的实数都有成立。
(1)求二次函数解析式;
(2)若二次函数图象与直线:只有一个公共点,求的值。
2. 直线:和双曲线的左支交于A、B两点,直线过点P()和AB线段的中点M,求在轴上的截距的取值范围。
3. 某汽车厂有一条价值为万元的汽车生产线,现要通过技术改造来提高该生产线的生产能力,提高产品的增加值,经过市场调查,产品的增加值万元与技术改造投入万元之间满足:① 与和的乘积成正比;② 当时,,并且技术改造投入比率:,其中是常数,且。
(1)设,求的表达式及定义域;
(2)求出产品增加值的最大值及相应的的值。
【试题答案】
一.
1. A
解析:由图象平移知识,可知可由向右平移3个单位产生,再将向下平移1个单位即得的图象。
2. D
解析:由,可知的图象关于直线对称,因而它的图象与轴的交点也关于直线对称,设这三根从小到大依次为,则,,∴ 三根之和为3。
3. A
解析:首先作出的图象,再作轴下方的图象关于轴的对称图象,再将轴下方图象去掉。
4. D
解析:讨论去掉绝对值:时,;
时,
观察图象知选D。
5. B
解析:由图象知,BC=4,CD=9-4=5,AD=14-9=5
故
故
6. C
解析:9年后即计算机价格连续三次降价,故9年后的价格为元
7. B
解析:设甲地销售辆,则乙地销售辆,总利润
对称轴,当时,取最大值
8. D
解析:若经秒人刚好追上汽车,则
由,得
此方程无解,即人不可能追上汽车
考虑距离差
故当时,有最小值7,即人与汽车最少相距7米,故选D。
二.
1. 解析:
(1)∵
又为二次函数 ∴ 可设
又当时, ∴ ∴
令,得 ∴
又 ∴ ,即
(2)由条件知,即
∴ ,即
2. 解析:将代入,得
整理,得
设,由题意得
解之,得
设AB的中点M为()
由题意知
即M()
易求得直线的方程为
故
令,易知
∴ ,即截距的取值范围为
3. 解析:
(1)由题意,设,又时,,故
解得
由,解得
故,定义域为(0,
(2),令,得,即在上为增函数
① 当,即,时,取得最大值
② 当,即,时,取得最大值
 爱华网
爱华网