直线、平面、简单几何体
【模拟试题】
第I卷(选择题 共60分)
一. 选择题(本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1. (青岛统测)已知直线与平面满足,,,那么必有( )
A. 且 B. 且
C. 且 D. 且
2. (知识原创题)若A、B、C、D四点满足AB⊥CD、AC⊥BD、AD⊥BC,则这四点的位置关系是( )
A. 一定共面 B. 一定不共面
C. 不一定共面 D. 不存在
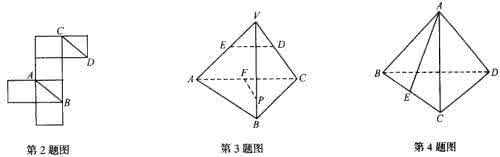
3. (郑州二次质量预测)正四棱锥P—ABCD的所有棱长都相等,E为PC的中点,那么异面直线BE与PA所成角的余弦值等于( )
A. B. C. D.
4. (知识交汇题)已知相交直线都在平面内,并且都不在平面内,若中至少有一条与相交;与相交,则p是q的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 不充分也不必要条件
5. (热点创新题)若正三棱锥的侧面都是直角三角形,那么侧面与底面所成的角的余弦值是( )
A. B. C. D.
6. (北京西城抽测)球O的截面把垂直于截面的直径分成1:3两部分,若截面圆半径为,则球O的体积为( )
A. B. C. D.
7. (济南统测)如图,正方体ABCD—中,E、F分别是AB、的中点,则异面直线与EF所成角的余弦值为( )
A. B. C. D.
8. (南京模拟)四棱锥P—ABCD,AD⊥面PAB,BC⊥面PAB,底面ABCD为梯形,AD=4,BC=8,AB=6,,满足上述条件的四棱锥的顶点P的轨迹是( )
A. 圆 B. 不完整的圆 C. 抛物线 D. 抛物线的一部分
9. (知识创新题)把一副三角板ABC与ABD摆成如下图所示的直二面角D—AB—C,则异面直线DC与AB所成的角为( )
A. B. C. D.
10. (易错警醒题)已知正四棱锥的侧棱与底面成角,则此四棱锥的两个相邻侧面所成的二面角的余弦值是( )
A. B. C. D.
11. (苏锡常镇调查一)设为两条直线,为两个平面,给出下列四个命题,其中,正确命题的个数是( )
① 若,则
② 若,则
③ 若,则
④ 若,则
A. 0个 B. 1个 C. 2个 D. 3个
12. (知识原创题)若,,如果与为共线向量,则( )
A. B.
C. D.
第II卷(非选择题 共90分)
二. 填空题(本大题共4小题,每小题4分,共16分。把答案填在题中横线上。)
13. (基本概念题)设,,,且点B的坐标为,则点A的坐标为 。
14. (知识创新题)是用“斜二测画法”画出的等腰直角三角形ABC的直观图,设的面积为,的面积为S,则 。
15. (条件开放题)以正方体的8个顶点中4个为顶点,且4个面均为直角三角形的四面体是 (只要写出一个四面体即可)。
16. (真题·辽宁卷)如图,正方体的棱长为1,C、D分别是两条棱的中点,A、B、M是顶点,那么点M到截面ABCD的距离是 。
三. 解答题(本大题共6小题,共74分。解答应写出文字说明、证明过程或演算步骤。)
17. (本小题满分12分)
(湖北八校二次联考)如图,在多面体ABCDE中,AE⊥面ABC,BD//AE,且AC=AB=BC=BD=2,AE=1,F为CD中点。
(1)求证:EF⊥面BCD;
(2)求面CDE与面ABDE所成的二面角的余弦值。
18. (本小题满分12分)
(成都二诊)如图,已知四棱锥S—ABCD的底面ABCD是正方形,SA⊥底面ABCD,E是SC上的一点。
(1)求证:平面EBD⊥平面SAC;
(2)设SA=4,AB=2,求点A到平面SBD的距离;
(3)当的值为多少时,二面角B—SC—D的大小为。
19. (本小题满分12分)
(高考变式题)如下图,已知是直三棱柱,D是AC的中点,O是的中点,E在上,且,AC=BC=CE=2,,。
(1)证明:截面BDE//AO;
(2)求三棱锥的体积。
20. (本小题满分12分)
(思维拓展题)
图(1)是一个正方形的表面展开图,MN和PQ是两条面对角线。请在图(2)的正方体中将MN、PQ画出来,并就这个正方体解答下列各题。
(1)求MN与PQ所成角的大小;
(2)求四面体M—NPQ的体积与正方体的体积之比;
(3)求二面角M—NQ—P的大小。
21. (本小题满分12分)
(经典常考题)如下图,在正方体中,E、F分别是、的中点。
(1)求异面直线与所成角的余弦值;
(2)设P为的中点,问:在上是否存在一点Q使得,若存在指出Q点的位置,若不存在说明理由。
22. (本小题满分14分)
(知识原创题)已知直棱柱,底面四边形ABCD是直角梯形,上底边长AD=6,直角边所在的腰AB=2,BC=2,,G是CD的中点,E是的中点,F在AD上,且。
(1)求异面直线EF与所成的角;
(2)求直线EF和平面所成的角;
(3)求二面角的大小。
【试题答案】
一.
1. A
解析:由已知,,可得,又,得,故得答案A。
2. C
解析:点A可以是的垂心,也可以是平面外的一点,使得三棱锥A—BCD的三条侧棱两两垂直,即此四点的位置关系是不一定共面,应选C。
3. D
解析:设O为底面正方形的中心,连结EO,有EO//PA,则是异面直线BE与PA所成的角。设正四棱锥P—ABCD的棱长为2,则在中,,,,故选D。
4. C
解析:本题将直线,平面知识与简易逻辑知识相结合,体现了在知识交汇处命题的高考趋势,从p出发能推到q,从q出发也能推出p,所以p是q的充分必要条件,故选C。
5. D
解析:如图,V—ABC是正三棱锥,所以顶点V在底面的射影O点为正三角形的中心,即O在AM上,M为BC的中点,连结VM,则为侧面与底面所成的角,设,,又为等腰直角三角形,
∴ 故选D
6. C
解析:设直径被分成的两部分分别为,易知,得,则球O的半径R=2,故。
7. B
解析:建立如图坐标系,设正方体的边长为2,则,E(2,1,0),F(0,2,1),C(0,2,0),,,
则
所以异面直线与EF所成角的余弦值为,故选B。
8. B
解析:由AD⊥面PAB及BC⊥面PAB,可得AD//BC,,又,及AD=4,BC=8,可得,即得,在平面PAB内以AB所在直线为x轴,AB中点O为坐标原点,建立直角坐标系,则,B(3,0),设点P的坐标为,则有
,整理可得一个圆方程,由于点P不在直线AB上,故此轨迹为一个不完整的圆,故应选B。
9. B
解析:过点C作CE//AB,过点A作AF⊥CE于点F,连结DF,设AD=1,则,,在中,,,故选B。
10. D
解析:如图,正四棱锥S—ABCD,作BH⊥SC于H,连结HD,则为所求二面角的平面角,设底面边长为1,则,,在中,由余弦定理得,故选择D。
易错点是错误理解“此四棱锥的两个相邻侧面所成的二面角”而错选A。
11. B
解析:① 由,,,可得或或相交,相交时只需都与交线平行;② 线线平行的判定;③ 必须;④ 由,要得到,必须有垂直于与的交线,故选B。
12. C
解析:若与共线,则有
∴ ,故应选C。
二.
13.
解析:
∴ 点A的坐标为
14.
解析:设原等腰直角三角形的底边长为,高为,则利用斜二测画法画成的三角形底边长不变,高为 ∴
15.
解析:如图,侧棱与上下两个底面垂直,则与底面内的任一直线垂直,连结AC,则,同理。
16.
解析:由等体积法求解,设点M到平面ABCD的距离为x,
∴
三.
17. (1)取BC中点G,连结FG、AG
∵ AE⊥面ABC,BD//AE ∴ BD⊥面ABC
又AG面ABC ∴ BD⊥AG
又AC=AB,G是BC中点 ∴ AG⊥BC
∴ AG⊥平面BCD
∵ F是CD的中点且BD=2 ∴ FG//BD且FG=1
∴ FG//AE
又AE=1 ∴ AE=FG,故四边形AEFG是平行四边形,从而EF//AG
∴ EF⊥面BCD
(2)取AB的中点H,则H为C在面ABDE上的射影,过C作CK⊥DE于K,连结KH,由三垂线定理的逆定理得KH⊥DE
∴ 为二面角C—DE—B的平面角
易知,,,
由
可得,中,,故
∴ 面CDE与面ABDE所成的二面角的余弦值为
18. (1)∵ SA⊥底面ABCD,底面ABCD ∴ SA⊥BD
∵ ABCD是正方形 ∴ AC⊥BD
∴ BD⊥平面SAC 又BD平面EBD
∴ 平面EBD⊥平面SAC
(2)设,连结SO,则SO⊥BD
由AB=2,知,
∴
∴
令点A到平面SBD的距离为h,由SA⊥平面ABCD
则 ∴
∴ 点A到平面SBD的距离为
(3)设SA=,建立如图所示空间直角坐标系,为计算方便,不妨设AB=1,则C(1,1,0),S(0,0,),B(1,0,0),D(0,1,0)
∴ ,,
再设平面SBC和平面SCD的法向量分别为,,则
∴ ,取,则 ∴ 可得
又
∴ ,取,则
∴ 可取 ∴
要使得二面角的大小为,则,从而,即当时,二面角B—SC—D的大小为
19. (1)设G为的中点,连结DF、OG,则,
∴ OG//BE 易知F为OC中点,又D为AC中点 ∴ AO//DF
又∵ 面BDE ∴ AO//截面BDE
(2)∵ 是直三棱柱, ∴ BC⊥侧面
∴ 侧面⊥侧面
设O到侧面的距离为h,则h等于O到侧面的距离
又∵ O为的中点
∴
故
20. (1)连结MC、NC,可得PQ//NC,则就是异面直线MN与PQ所成的角
∵ 是等边三角形 ∴
则MN与PQ所成的角等于
(2)不失一般性,设正方体的棱长为1,则(立方单位)
∵ (立方单位)
∴
(3)∵ PN⊥平面AQMP ∴ 平面MPQ⊥平面NPQ
作MO⊥PQ于O,ME⊥NQ于E,连结OE,并设正方体的棱长为1,则MO⊥平面NPQ
∵ OE是ME在平面NPQ内的射影
∴ OE⊥NQ
则是二面角M—NQ—P的平面角
由~,得 ∴
∵ MO⊥OE ∴
∴
则二面角M—NQ—P的大小为
21. (1)以点D为坐标原点,DA为x轴,DC为y轴,为z轴建立空间直角坐标系,设正方体的棱长为,则A(,0,0),,,
∴ ,
∴
∴ 异面直线与所成角的余弦值为
(2)假设存在点使得
∴ ,,
∴ ,,,则
∴ 存在点,且时,
22. 以A为原点,分别为所在的直线为x轴,y轴,z轴,建立空间直角坐标系,则C(2,2,0),D(0,6,0),G(1,4,0),,F(0,2,0),E(2,2,2)
(1),
∴
即与所成的角为
所以异面直线EF与所成的角为
(2)取,连结,则H(0,2,4),
∵ 平面 ∴ 是EF在平面上的射影
∵ ∴
∴ 直线EF与平面所成的角为
(3)过E作EP⊥FG于P,过作于Q
∵ P、Q在平面内,且在直线FG上,在平面内FG的方程为
故可设P、Q点坐标为,
则,,
∵ ∴ ∴
又∵ ∴ ∴
∴ ,
∴
∴ 二面角E—FG—D1的大小为
 爱华网
爱华网


