第三章 半导体中载流子的统计
半导体靠电子和空穴传导电流,为了了解和描述半导体的导电过程,必须首先了解其中电子和空穴按能量分布的基本规律,掌握用统计物理学的方法求解处于热平衡状态的一块半导体中的载流子密度及其随温度变化的规律。这就是本章要讨论的主要问题。
§3.1 状态密度
为了计算半导体中热平衡载流子的密度及其随温度变化的规律,我们需要两方面的知识:第一,载流子的允许量子态按能量如何分布;第二,载流子在这些允许的量子态中如何分布。
一、 热平衡状态下的电子和空穴
1、 热平衡状态
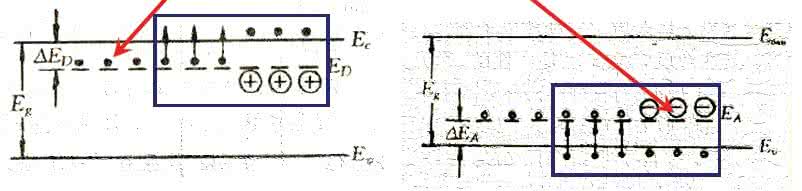
在一定温度下,如果没有其他外界作用,半导体中能量较低的价带和施主能级上的电子依靠热激发跃迁到能量较高的受主或(和)导带,分别在价带和导带中引入可以导电的空穴和电子。同时,高能量状态上电子也有一定的几率退回到它原来的低能量状态。于是,电子和空穴在所有允许量子态间的可逆跃迁达到稳定的动态平衡,使导带和价带分别具有稳定的电子密度和空穴密度,这种状态即是热平衡状态。
处于热平衡状态下的导带电子和价带空穴称为热平衡载流子。热平衡载流子具有稳定的、与温度相关的密度。因此,需要解决如何计算确定温度下半导体热平衡载流子密度的问题。
2、 热平衡状态下的载流子密度
由于导电电子和空穴分别分布在导带和价带的量子态中,所以电子和空穴的密度必取决于这些状态的密度分布,以及电子和空穴占据这些状态的几率。如果状态密度是与能量无关的常数NC和NV,则电子和空穴的热平衡密度n0和p0直接由NC和NV分别与相应的几率函数相乘得出;如果状态密度是能量的函数gC(E) 和gV(E),则载流子密度的计算须采用积分方式,即
n0?
?
?
EC
gC(E)f(E)dE;p0?
?
EV
??
gV(E)f(E)dE
因此,须了解态密度函数和几率函数的具体函数形式。 二、 态密度的定义及求解思路
假定在能带中无限小的能量间隔dE内有dZ个量子态,则状态密度g(E)定义为
g(E)?dZ/dE
也就是说,状态密度g(E)就是在能带中能量E的附近每单位能量间隔内的量子态数。
由上式看出,为了求解态密度函数g(E)的具体形式,须求出k空间中状态分布与能量的函数关系。为此,要首先算出单位体积k空间中的量子态数,即k空间的量子态密度;然后算出k空间中某能量范围对应的k空间体积,二者相乘方可得到相应的状态数Z, 对Z取微商即得g(E)。
三.K空间的量子态密度
在第一章的讨论中我们知道,半导体中电子的允许能量状态(即能级)用波矢k标志,有界晶体中电子波矢k的取值受到边界条件的限制。对晶格常数为a,原胞数为N的一维晶体,k的允许值为简略布里渊区中N个等间距的点,间隔距离为1/L,L=Na,即一维晶体的长度。由此可知,一维晶体k空间的量子态密度就是它的长度L。
如此类推,用同样的方法可以算出体积为V=L3的晶体的三维k空间的量子态密度是V。 如果计入电子的自旋,k空间一个点实际上代表自旋方向相反的两个量子态。这时,电子在k空间的允许量子态密度是2V。
四、状态密度
1、 导带底的状态密度 1)各向同性的情况
首先考虑能带极值在k=0,等能面为球面的各向同性情况。已知其导带底附近E(k)关系为
在k空间中,以│k│为半径作一球面,它就是能量为E(k)的等能面,相应的球体体积是
43
?k?
3
43
?
(2mn)
h
3
?3/2
(E?EC)
3/2
已知k空间中量子态密度是2V,所以动能小于?=E-EC的状态数(球体内状态数)就是
Z?
83
?V
(2mn)
h
3
?3/2
(E?EC)
3/2
上式对能量取微分,得
dZ?4?V
(2mn)
h
3?
3/2
(E?EC)
1/2
dE
按定义得各向同性导带底单位能量间隔中的状态数(态密度)
gC(E)?
dZdE
?4?V
(2mn)
h
3?
3/2
(E?EC)
1/2
上式表明,导带底附近单位能量间隔内的量子态数目随着能量增加按抛物线关系增大,而且与电子的有效质量有关,有效质量较大的带,态密度较高。
通常将态密度定义为单位体积单位能量间隔内的量子态数目,因而上式中V=1。 2)各向异性的情况
对于导带底不在布里渊区中心,且电子等能面为旋转椭球面的各向异性问题可用类似的方法得到相似的结果。问题的关键在于求出旋转椭球等能面的体积。
对这种情况下,已知其导带底附近E(k)关系为
E(k)?EC
2222
k3?h?k1?k2
?? ???2?mtml??
已知椭球体积为
4?3abc
式中a、b、c分别为椭球的长短轴之半,其值分别为
a?
(2ml)
h
1/2
(E?EC)
1/2
;b?c?
(2mt)
h
1/2
(E?EC)
1/2
于是知,一个椭球内动能小于?=E-EC的状态数就是
Z?
83
?V
(8mlmt)
h
3
21/2
(E?EC)
3/2
于是,具有s个等价能谷的各向异性导带的态密度就是
gC(E)?4?Vs
(8mlmt)
h
32
1/2
(E?EC)
1/2
?4?V
(2mdn)
h
3
3/2
(E?EC)
1/2
令s(8mlmt2)1/2=(2mdn)3/2,上式最终写成跟各向同性导带相同的形式:
mdn?s
2/3
(mlmt)
21/3
称mdn为导带底电子的态密度有效质量。对硅,s=6,其mdn=1.08m0;对锗,s=4,其mdn=0.56 m0。
2、价带顶的状态密度 (1) 无简并的情况
考虑价带顶位于布里渊区中心且各向同性,中心附近的E(k)关系为
E(k)?EV?
h(kx?ky?kz)
2m
2
p
2
2
2
2
球形等能面的半径为
(2mp)
h
*
1/2
(EV?E)
1/2
mp*为价带顶空穴有效质量。用同样的方法算得价带顶附近状态密度gv(E)为
gV(E)?4?V
(2mp)
h
3*
3/2
(EV?E)
1/2
(2) 对轻、重空穴的考虑
在晶体硅、锗中,价带在价带顶是二度简并的;与这两个能带相对应的有轻空穴有效质量(mp)l
和重空穴有效质量(mp)h。因而,价带顶附近状态密度应为这两个能带的状态密度之和。相加之后,价带顶附近gV(E)仍可由式(3-8)表示,不过要将其中的有效质量mp*替换为
mdp?(mp轻?mp重)
3/2
3/2
2/3
称mdn为价带顶空穴的态密度有效质量。对硅,mdp=0.59 m0;对锗,mdp=0.37 m0。
§3.2 费米能级和载流子的统计
一、费米分布函数
1、量子态的占据几率
在热平衡状态下,电子在不同能量量子态上的分布几率是一定的。根据量子统计理论,服从泡利不相容原理的电子遵循费米统计律,能量为E的一个量子态被电子占据的几率
f(E)?
1?exp(
1E?EF
kT
)
f(E)被称为电子的费米分布函数。式中k是玻耳兹曼常数,T是热力学温度。
f(E)表示能量为E的量子态被电子占据的几率,那么1- f(E)就是能量为E的量子态不被电子占据的几率,若该量子态属于价带,这也就是它被空穴占据的几率。即
1?f(E)?
1?exp(
1EF?EkT
)
2、量子态在不同温度下被电子占据的几率 (1)T=0K时
若E<EF,则f(E)=1,即这些量子态是满的;
若E>EF,则f(E)=0,因而这些量子态是空的。 (2)T>0K时
若E<EF,则f(E)>l/2,即能量比费米能级低的量子态被电子占据的几率较大
若E=EF,则f(E)=l/2,即能量等于费米能级的量子态被电子占据的几率是50%;
若E>EF,则f(E)<l/2,即能量比费米能级高的量子态被电子占据的几率较小。
可以认为,在温度不很高时,能量大于费米能级的量子态基本上没有被电子占据,而能量小于费米能级的量子态基本上为电子所占据,而电子占据费米能级的几率在各种温度下总是1/2,所以费米能级的位置比较直观地反映电子占据量子态的水平。
图3-3中给出了温度300K、1000K和1500K时的费米分布函数曲线。图中可见,随着温度的升高,电子占据费米能级以下能量状态的几率下降,而占据费米能级以上能量状态的几率增大。
图 3-3 费米分布函数与温度关系曲线 (曲线A,B,C,D分别是0K, 300K, 1000K, 1500K的f(E)曲线)
二、费米能级
费米分布函数中的参量EF被称为为费米能级或费米能量,其大小与温度、材料的导电类型、杂质的含量以及能量零点的选取有关。在一定温度下,EF决定电子在各量子态上的统计分布。
1、 费米能级位置的确定
在确定温度下,量子态被电子占据的难易程度决定于其能级与费米能级的相对位置,因而确定费米能级的位置是载流子统计的前提。
按定义,一个电子系统内所有被电子占据的量子态数目之和应等于该系统的电子总数N,即
?N
i
i
f(Ei)?
?
i
f(Ei)?N
如果一个电子系统中没有相同的状态对应于同一能量,则上式中Ni=1。利用此关系即可确定费米能级在能带结构中的位置。
2、 费米能级的物理含义
将半导体中大量电子的集合看成一个热力学系统,由统计理论证明,费米能级EF是系统的化学势,即
EF???(
?F?N
)T
在统计物理学中,μ代表系统的化学势,F是系统的自由能。上式的意义在于:当系统处于热平衡状态,也不对外界做功的情况下,系统中增加一个电子所引起系统自由能的变化,等于系统的化学
势,也就是等于系统的费米能级。处于热平衡状态的系统有统一的化学势,所以,处于热平衡状态
百度搜索“爱华网”,专业资料、生活学习,尽在爱华网!
 爱华网
爱华网