两个平面位置关系复习
二. 知识讲解:
1. 两个平面的位置关系
(1)两个平面平行——没有公共点()
(2)两个平面相交——有一条公共直线()
2. 两个平面平行的判定定理
(1)如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行
(书例题)
(2)垂直于同一条直线的两个平面平行
3. 两个平面平行的性质定理
(1)如果两个平行平面同时和第三个平面相交,那么它们的交线平行
(2)如果两个平面平行,那么其中一个平面内的直线平行于另一个平面
(例题)
(3)如果一条直线垂直于两个平行平面中的一个平面,那么它也垂直于另一个平面
4. 两个平行平面的距离
和两个平行平面同时垂直的直线,叫做两个平行平面的公垂线,它夹在这两个平行平面间的部分叫做两个平行平面的公垂线段。
可以证明,公垂线段都相等,定义公垂线段的长度叫做两个平行平面的距离。
5. 两个平面垂直的定义
两个平面相交,如果它们所成的二面角是直二面角就说两个平面互相垂直,记作。
6. 两个平面垂直的判定定理
如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直
7. 两个平面垂直的性质定理
如果两个平面垂直,那么在一个平面内垂直于它们交线的直线垂直于另一个平面
8. 二面角
(1)二面角的概念
① 二面角定义:从一条直线出发的两个半平面所组成的图形叫做二面角。
② 二面角的平面角:以二面角的棱上任意一点为端点,在两个半平面内分别作垂直于棱的两条射线,这两条射线所成的角。
③ 二面角大小可用其平面角来度量,取值范围
(2)方法提要:作二面角平面角的方法
① 利用二面角平面角的定义
② 利用三垂线
③ 作棱的垂面
(3)二面角平面角的求法
① 定义法:利用图形中的已知点作出二面角的平面角后,通过一个或几个可解的直角三角形或斜三角形解得
② 利用射线面积公式
③ 利用异面直线上两点间距离公式
【典型例题】
[例1] 如果两个平面垂直,则经过第一个平面内的一点垂直于第二个平面的直线在第一个平面内。
证:设,则有两种情形和,经过A在内作
由,而
又由经过一点A有且只有一条直线与垂直,故AB与重合,故
[例2] 已知,PA⊥面ABC,PA=AB=BC=,求二面角A—PC—B的大小。
解:过A作AD⊥PB交PB于D(可以证明,AD⊥平面PBC)
由
过D作DE⊥PC于E,连AE,则AE⊥PC
故为二面角A—DC—B的平面角
在等腰中,,由,则
故
另法可证为二面角A—PC—B的平面角
在中,
又法
[例3] 如图,和都是直角三角形,AB=BC,,把沿AC折起,使所在平面与所在平面垂直,若AB=,求C点到平面ABD的距离。
解:∵ 面ABC⊥面ACD,且交线为AC,DC平面ACD
DC⊥AC ∴ DC⊥面ABC ∴ DC⊥AB
∵ AB⊥BC, ∴ AB⊥面BCD
∴ 面ABD⊥面BCD且交线BD
过C作CH⊥BD于H,则CH⊥面ABD
∵ AB=BC=, ∴
在中,
在中,
∴
[例4] 四边形ABCD中,AD//BC,AD=AB,,将沿对角线BD折起,记折起后A的位置为P,且使平面PBD⊥平面BCD。
(1)求证:CD⊥平面PBD;
(2)求证:平面PBC⊥平面PDC;
(3)求二面角P—BC—D的大小。
证:(1)
(2)
(3)
作EF⊥BC于F,连结PF,则为二面角P—BC—D的平面角
,即二面角P—BC—D的大小为
另法,又由
[例5] 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F。
(1)证明PA//平面EDB;
(2)证明PB⊥平面EFD;
(3)求二面角C—PB—D的大小。
方法一:(1)证明:连结AC,AC交BD于O,连结EO
由底面ABCD是正方形O是AC的中点
在中,EO是中位线PA//EO
而EO平面EDB且平面EDBPA//平面EDB
(2)证明:
(3)解:由(2)知,PB⊥DF,故是二面角C—PB—D的平面角
由(2)知DE⊥EF,PD⊥DB
设正方形ABCD的边长为,则PD=DC=,BD=
,
在中,
在中,
则,所以,二面角C—PB—D的大小为
另法
[例6] 如图,在中,,CD是的平分线,AC=6,BC=4,沿CD将折起到的位置,使,求二面角的大小。
解:过B、A两点分别向CD及其延长线作垂线BE,AF,垂足分别为E、F
在中,,
在中,,
∴
设CD折起后,设二面角的大小为
由
∴ 即二面角大小是
注1:当异面直线分别在两个相交的半平面内,它们的公垂线在棱上时,由异面直线上两点距离公式,易知此处是二面角大小。
注2:这种求二面角的方法,避开了平面角的作图
【模拟试题】
一. 选择题:
1. 一个平面内的两条直线分别平行于另一个平面是两个平面平行的( )
A. 充分条件 B. 必要条件 C. 充要条件 D. 既不充分也不必要条件
2. 正方体中,以每两条棱确定的平面中,与对角面垂直的平面有( )
A. 1个 B. 2个 C. 3个 D. 4个
3. 已知下列四个命题,其中真命题的个数为( )
(1)直线上有三个不同的点到平面的距离都相等,则;
(2)过平面外三个不同的点,有且只有一个平面与垂直;
(3)三条共点的直线两两垂直,则所得的三个平面两两垂直;
(4)直线和平面都成等角,则
A. 0个 B. 1个 C. 2个 D. 3个
4. 在一个锐二面角的一个面内有一点,它到棱的距离等于它到另一个面距离的2倍,则这个二面角的度数为( )
A. 30° B. 45° C. 60° D. 以上都不对
5. 一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,则这两个二面角( )
A. 相等 B. 互补 C. 相等或互补 D. 不能确定
6. 一条线段与一个直二面角的两个面都相交,这条线段与这两个平面所成角的和为( )
A. 90° B. 不大于90° C. 大于90° D. 不小于90°
7. 分别表示不同的直线,表示不同的平面,下面四个命题中真命题的个数是( )
(1);
(2);
(3);
(4)
A. 1个 B. 2个 C. 3个 D. 4个
8. 直二面角的棱上取一点P,过P在内分别作与棱成角的射线,则两射线所成的角为( )
A. 45° B. 60° C. 120° D. 60°或120°
9. 在空间,下列命题中正确的是( )
A. 如果两直线与直线所成的角相等,那么
B. 如果两直线与平面所成的角相等,那么
C. 如果直线与两平面所成的角都是直角,那么
D. 如果平面与两平面所成的二面角都是直二面角,那么
10. 下列命题中正确命题的个数是( )
(1)过平面外一点有且只有一个平面平行于已知平面;
(2)过平面外一点有且只有一个平面垂直于已知平面;
(3)过直线外一点有且只有一个平面平行于已知直线;
(4)过直线外一点有且只有一个平面垂直于已知直线
A. 1个 B. 2个 C. 3个 D. 4个
11. 四面体的四个面中,直角三角形最多有( )
A. 1个 B. 2个 C. 3个 D. 4个
12. 已知直线平面,直线平面,有下面四个命题,正确的有( )
(1);
(2);
(3);
(4)
A.(2)与(4) B.(3)与(4) C.(1)与(2) D.(1)与(3)
二. 填空题
1. 在正方体中,点O是侧面正方形的中心,则平面AOB与平面AOC所成的二面角是 。
2. 若点A为直二面角的棱上一点,两条长都等于的线段AB、AC分别在内,且都与成,则BC的长为 。
3. 已知菱形ABCD的对角线AC=,沿BD把面ABD折起与面BCD成的二面角,则点A到面BCD的距离为 。
4. 已知空间四边形ABCD中,AB=BC,CD=DA=AC=,则二面角的大小为 ,二面角的大小为 。
5. 是正三角形,P是外一点,PA=PB=PC,若,则二面角的大小为 。
6. 已知,,于M1,,NA是的斜线,若NA⊥MN,MN=,NA=,M1A=,则 。
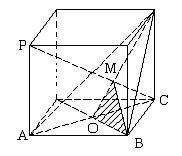
7. 正方体中M、N分别是棱和的中点,则面BMN与面ABCD所成二面角的正切值等于 。
8. 已知是直线,是平面,给出下列命题
(1)若垂直于内的两条相交直线,则;
(2)若平行于,则平行于内的所有直线;
(3)若,且,则;
(4)若,且,则;
(5)若,且,则。其中正确的命题的序号是 。
【试题答案】
一. 选择题:
1. B
2. C
提示:含两个底面和一个对角面共有三个平面。
3. C
提示:命题(1)和(3)是真命题。
4. A
5. D
提示:当满足题设的两个二面角的棱不平行时,这两个二面角的大小关系不确定。
6. B
提示:可用特殊情形验证。当线段有一个端点在棱上时也满足题设条件,此时线段在二面角的一个面内,则线段与这个平面所成的角为0°,因此线段与二面角两个面所成角之和即为线段与另一个面所成的角,故应选B,并且当线段与另一个面垂直时取得90°。
7. A
提示:只有命题(4)是真命题
8. D
提示:由于是两射线所成的角,故应分锐角和钝角两种情形。
9. C
10. B
提示:命题(1)和(4)是正确的,而(2)和(3)是错误的。
11. D
提示:如答图所示,AB⊥平面BCD,为,,则由三垂线定理可知AC⊥CD,则也为。因此四面体ABCD的四个面可以都是直角三角形,故选D。
12. D
二. 填空题:
1. 90°
提示:由OC⊥OB,又OC⊥OAOC⊥平面AOB,又OC平面AOC,故平面AOB⊥平面AOC。
2. 或
提示:设直线AB与AC所成锐角为,则,故,
当时,,
当时,,
故BC的长为或
3.
提示:如答图1
即AH为A到面BCD的距离
由,则,在中,
答图1
4. 90°;
提示:如答图2所示,取E为BD的中点,连结AE、CE则AE⊥BD,CE⊥BD。即为二面角A—BD—C的平面角,,,AC=,
则由知
取F为BC中点,连结EF、AF
即为二面角A—BC—D的平面角
,则
答图2
5. 60°
提示:设P在上的射影为O,由PA=PB=PC,则O为正的中心,则,故,故
6.
提示:如答图3,作于A1,连结。由,则由三垂线定理的逆定理知。
在中,,则
在中,AN=C,则
在中,M1M=AA1则
答图3
7.
提示:如答图4,设面BMN交棱A1D1于F,由于,则
设FN与DA延长线相交于E,则BE为面BMN与面ABCD所成二面角的棱
作AH⊥BE于H,连NH,则为所求二面角的平面角,设正方体棱长为
在中,
在中,,故所求二面角的正切值为
答图4
8.(1)(4)
提示:由线面垂直的判定定理知(1)正确。又由面面垂直的判定定理知(4)正确。
 爱华网
爱华网