因子载荷a(
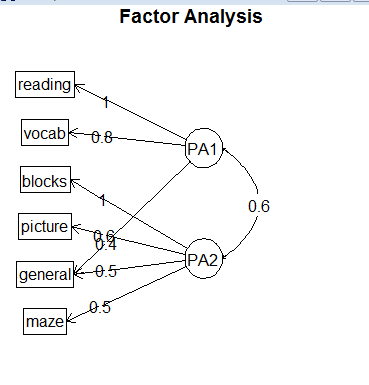
ij)的统计意义就是第i个变量与第j个公共因子的相关系数即表示X(i)依赖F(j)的份量(比重)。统计学术语称作权,心理学家将它叫做载荷,即表示第i个变量在第j个公共因子上的负荷,它反映了第i个变量在第j个公共因子上的相对重要性。
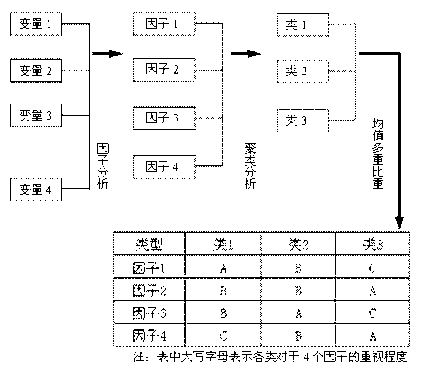
在因子分析中,通常只选其中m个(m<p主因子),即根据变量的相关选出第一主因子?1,使其在各变量的公共因子方差中所占的方差贡献为最大,然后消去这个因子的影响,而从剩余的相关中,选出与之不相关的因子,使其在各个变量的剩余因子方差贡献中为最大,如此往复,直到各个变量公共因子方差被分解完毕为止。
为了理解因子分析的原理,我们讨论与因子载荷有关的一些量的统计意义。
在因子模型中,假定原始变量、公共因子和特殊因子都已标准化,即平均值为0,方差为1。每一个变量xi的方差为:
Dxi = a2i1D?1 + a2i2D?2 + … + a2imD?m + a2i Dε
2222i = h2i + a2i = 1 其中hi
=ai1+ai2+…+aim,为因子载荷矩阵中第i行元素的平方和,称为共同度。因
此,变量xi的方差由两部分组成,第一部分为共同度hi2,它是全部公因子对变量xi的总方差的贡献,如公因子的方差接近1,则说明该变量的几乎全部信息都被所选取的因子说明了;第二部分是特殊因子的方差,仅与变量xi本身的变化有关。
公因子的方差的意义在于说明当由原始变量空间转化为因子空间后,保留原来各变量的信息有多少,当hi越接近1时,说明空间转化性质越好。 2
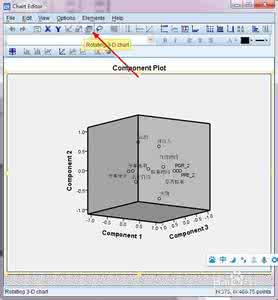
公因子的方差的意义在于说明当由原始变量空间转化为因子空间后,保留原来各变量的信息有多少,当hi越接近1时,说明空间转化性质越好。 2
因子载荷矩阵中各列元素的平方和为相应的公因子的方差贡献。它等于公因子所对应的特征值,即
它是衡量公因子相对重要性的指标。
最后,值得指出的是因子载荷α
ij表示第i个变量和第j个公共因子的相关系数。
 爱华网
爱华网