5.因式分解
因式分解★★ 把一个多项式化为几个整式的积的形式,叫做把这个多项式因式分解,也叫做把这个多项式分解因式.
★要点提示★
1.因式分解的对象是多项式,结果一定是积的形式.
2.结果中每一个因式必须是整式,且每个因式的次数都必须低于或等于原多项式的次数.
3.分解因式必须分解到不能再分解为止.
4.因式分解与整式乘法是互逆的关系,如
公因式 一个多项式中每一项都含有的因式叫做这个多项式的公因式.
提取公因式法★★★ 如果一个多项式的各项含有公因式,那么可以把该公因式提取出来作为多项式的一个因式,提出公因式后的式子放在括号里,作为另一个因式,这种分解因式的方法叫做提取公因式法.
★要点提示★
1.公因式的构成如下:①系数——取各项系数的最大公约数;②字母——取各项都含有的字母;③指数——取相同字母的最低次幂.
2.如果多项式的首项是负数时,一般应先提“-”号,使括号内第一项系数是正数,然后再对括号内的多项式进行提取公因式.
3.利用提取公因式法分解因式时,一定要提“干净”也就是说,提取后剩下的多项式不再有公因式.
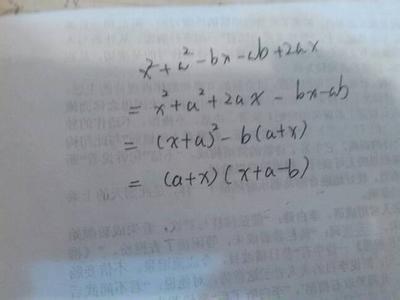
4.当某项就是公因式时,提取后剩下的“1”或“-1”不要漏掉.
公式法★★★ 逆用乘法公式将一个多项式分解因式的方法叫做公式法.
★要点提示★
1.运用公式法分解因式先要观察,如果的两项,考虑用平方差公式;如果是三项,考虑用完全平方公式.其次是多项式与公式的对应关系,什么是公式中的“a”,什么是公式中的“b”,然后才能运用公式.
2.一定要分解到不能再分解为止,如
a4-81=(a2+9)(a2-9),
就没有分解彻底.其中a2-9还可以分解为(a+3)(a-3).
3.合理变形,巧妙运用公式是一个难点.如分解因式(x-y)2-4(x-y-1),若将其变形为(x-y)2-4(x-y)+4后,就可以用完全平方公式分解因式了.
十字相乘法★★★ 利用十字交叉线来分解系数,把二次三项式切解因式的方法叫做十字相乘法.有
x2+(a+b)x+ab=(x+a)(x+b).
★要点提示★
1.用十字相乘法分解的多项式必须是二次三项式.
2.当二次项系数为1时,常采用的是“拆常数项,凑一次项”的方法.当常数项为正时,若一次项系数也为正,则把常数项分解为两个正的因数;若一次项的系数为负,则把常数项分解为两个负的因数.当常数项为负时,它分解后的两个因数异号;如果一次项系数为正,取绝对值较大的那个因数为正;若一次项的系数为负,取绝对值较大的那个因数为负.
分组分解法★★★ 利用分组来分解因式的方法叫做分组分解法.
★要点提示★
1.分组分解法主要应用于四项以上(包括四项)的多项式的因式分解.
2.分组的原则:
①分组后能直接提取公因式;
②分组后能直接运用公式.
3.常用的分组方法
①按字母分组;
②按系数分组;
③按次数分组.
 爱华网
爱华网