外心内心重心垂心外心、重心、垂心三点共线的证明-爱华网

内心没有分别心，就是真正的苦行(写心情的句子) 内心独白经典句子

我怀旧，因为我看不到你和未来。人生最遗憾的，莫过于，轻易地放弃了不该放弃的，固执地，坚持了不该坚持的。当你快乐时，你要想，这快乐不是永恒的。当你痛苦时你要想这痛苦也不是永恒的。他赏了你钱，所以他是好人；有了拍马的人，自然就有爱拍马的人

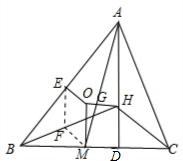
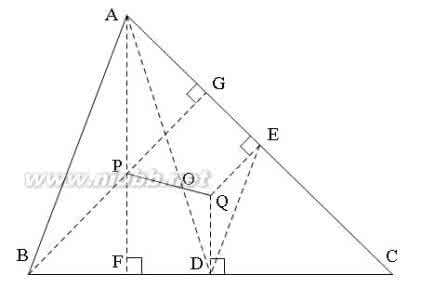
我用了两年时间系统详细研究三角形，先后证明三角形三条角平分线交于一点（内心）、三边垂直平分线交于一点（外心）、三条中线交于一点（重心）、三条高交于一点（垂心）。证明这些，最终是要为今天证明的这个命题做铺垫的。如果我都不能证有重心、垂心

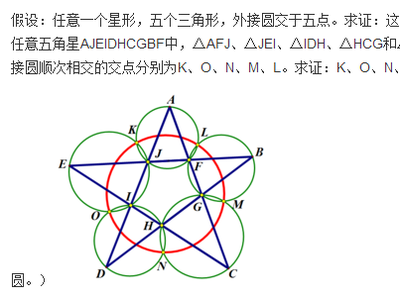
九点共圆，指的是三角形中，三边的中点、三条高的垂足、垂心到三顶点连线的中点，这九个点分布在同一圆上。这个定理看起来是很不好证的，但是如果先不把九个点都考虑进来，只考虑一边中点、一个垂足、垂心到一顶点连线中点这三点共圆，那是肯

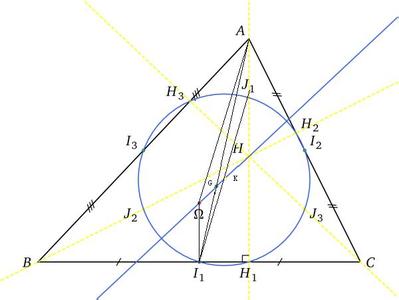
欧拉线是一个数学概念。欧拉线_欧拉线 -欧拉线概述欧拉线三角形的外心、重心、九点圆圆心、垂心，依次位于同一直线上，这条直线就叫三角形的欧拉线。欧拉于1765年在它的著作《三角形的几何学》中首次提出定理：三角形的重心在欧拉线上

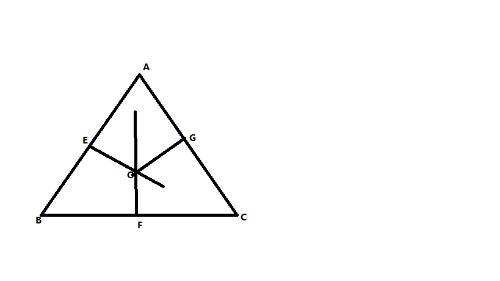
垂心是从三角形的各个顶点向其对边所作的三条垂线的交点。锐角三角形的垂心在三角形内；直角三角形的垂心在直角顶点上；钝角三角形的垂心在三角形外。三角形的垂心是它垂足三角形的内心；或者说，三角形的内心是它旁心三角形的垂心；垂心H关