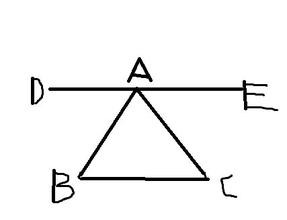
(1)∠DAB等于多少度?为什么?
(2)∠EAC等于多少度?为什么?
(3)∠BAC等于多少度?
(4)通过这道题,你能说明为什么三角形的内角和是180°?
题型:解答题难度:中档来源:不详
(1)∠DAB=44°.
理由:∵DE∥BC
∴∠DAB=∠B=44°(两直线平行,内错角相等);
(2)∠EAC=57°
理由:∵DE∥BC
∴∠EAC=∠C=57°(两直线平行,内错角相等);
(3)∠BAC=180°-∠B-∠C=79°;
(4)能说明三角形的内角和是180°.
理由:∵DE∥BC
∴∠DAB=∠B,∠EAC=∠C
∵∠DAB+∠EAC+∠BAC=180°
∴∠B+∠C+∠BAC=180°.
考点:
考点名称:平行线的性质,平行线的公理
平行公理:过直线外一点有且只有一条直线与已知直线平行。
推论(平行线的传递性):平行同一直线的两直线平行。
∵a∥c,c ∥b
∴a∥b。
平行线的性质:
1. 两条平行被第三条直线所截,同位角相等。
简单说成:两直线平行,同位角相等。
2. 两条平行线被第三条直线所截,内错角相等。
简单说成:两直线平行,内错角相等。
3 . 两条平行线被第三条直线所截,同旁内角互补。
简单说成:两直线平行,同旁内角互补。
①注意条件“经过直线外一点”,若经过直线上一点作已知直线的平行线,就与已知直线重合了;
②平行公理体现了平行线的存在性和唯一性;
③平行公理的推论体现了平行线的传递性。
④在两直线平行的前提下才存在同位角相等、内错角相等、同旁内角互补的结论。这是平行线特有的性质。不要一提同位角或内错角就认为他们相等,一提同旁内角就认为互补,若没有两直线平行的条件,他们是不成立的。
 爱华网
爱华网