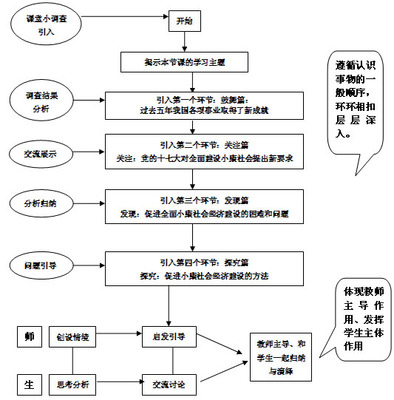
设{an}的公比为q,由S4=1,S8=17知q≠1,
∴得a1(q4-1)q-1=1①
a1(q8-1)q-1=17②
由 ①和②式
整理得q8-1q4-1=17
解得q4=16
所以q=2或q=-2
将q=2代入 ①式得a1=115,
∴a=2n-115
将q=-2代入 ①式得a1=-15,
∴an=(-1)n×2n-15,
综上所述an=2n-115或an=(-1)n×2n-15
考点:
考点名称:等比数列的通项公式等比数列的通项公式:
an=a1qn-1,q≠0,n∈N*。

等比数列的通项公式的理解:
①在已知a1和q的前提下,利用通项公式可求出等比数列中的任意一项;
②在已知等比数列中任意两项的前提下,使用可求等比数列中任何一项;
③用函数的观点看等比数列的通项,等比数列{an}的通项公式,可以改写为.当q>o,且q≠1时,y=qx是一个指数函数,而是一个不为0的常数与指数函数的积,因此等比数列{an}的图象是函数的图象上的一群孤立的点;
④通项公式亦可用以下方法推导出来:
将以上(n一1)个等式相乘,便可得到
⑤用方程的观点看通项公式.在an,q,a1,n中,知三求一。
等比数列的前n项和公式:
;
等比数列中设元技巧:
已知a1,q,n,an,Sn中的三个量,求其它两个量,是归结为解方程组问题,知三求二。
注意设元的技巧,如奇数个成等比数列,可设为:…,…(公比为q),但偶数个数成等比数列时,不能设为…,…因公比不一定为一个正数,公比为正时可如此设。
等比数列前n项和公式的变形:
q≠1时,(a≠0,b≠0,a+b=0);
等比数列前n项和常见结论:
一个等比数列有3n项,若前n项之和为S1,中间n项之和为S2,最后n项之和为S3,当q≠-1时,S1,S2,S3为等比数列。
 爱华网
爱华网